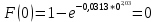Рисунок 4 - Гистограмма распределения наработки

Для построения графика статистической зависимости интенсивности отказов от времени в середине каждого интервала определяется значение интенсивности отказов по формулам







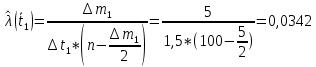
Таблица 6

	0,0342
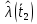	0,1858
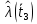	0,2444
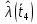	0,3599
	0,3983
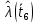	0,7339
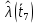	0,5881
	0,8690
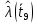	0,9724

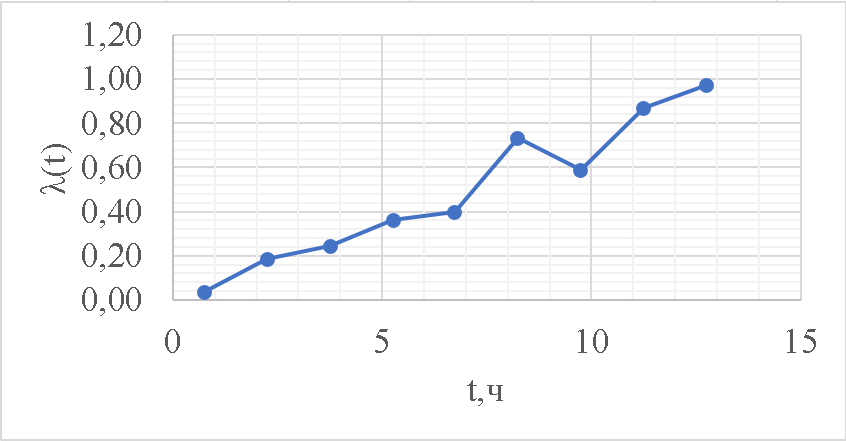
Рисунок 5 - График статистической функции интенсивности отказов

По графикам зависимостей выдвигаем гипотезы о том, что это нормальное распределение или распределение Вейбулла.

Определим параметры распределений.

Нормальное распределение является двухпараметрическим распределениям. Параметрами нормального распределения являются средняя наработка (математическое ожидание наработки) T₀ и среднеквадратическое отклонение .

Оценку средней наработки можно определить на основе данных вариационного ряда по формуле

---

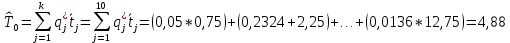
Дисперсию наработки объекта определим по формуле



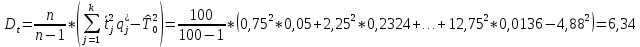
Оценка среднеквадратического отклонения находится по формуле



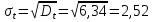
Распределение Вейбулла является двухпараметрическим распределением. Этими параметрами являются параметр формы η и параметр масштаба µ.

Коэффициент вариации в случае распределения Вейбулла



Где 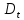– дисперсия наработки объекта



Используя метод моментов, приравняем статистическое значение коэффициента вариации 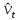его точному значению 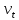, по таблице зависимости ν(η) для распределения Вейбулла определим значение параметра формы 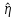, соответствующее полученному значению 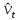, а затем определим значение коэффициента масштаба с помощью формулы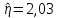





Подставляя полученные параметры в формулы временных зависимостей для соответствующих законов распределений, построим статистические графики.

Нормальное распределение









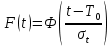
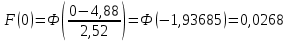
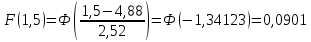
Таблица 7

t
0	-1,9368	0,0268
1,5	-1,3412	0,0901
3	-0,7456	0,2297
4,5	-0,15	0,4404
6	0,4456	0,67
7,5	1,0412	0,8508
9	1,6368	0,9495
10,5	2,2324	0,9861
12	2,8280	0,9974
13,5	3,4237	1

---

Рисунок 6 - Функция распределения наработки; - ; -









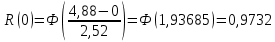
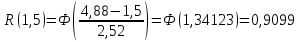
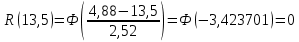
Таблица 8

t
0	1,9368	0,9732
1,5	1,3412	0,9099
3	0,7460	0,7703
4,5	0,1507	0,5596
6	-0,4444	0,33
7,5	-1,0396	0,1492
9	-1,6368	0,0505
10,5	-2,2324	0,0139
12	-2,8280	0,0026
13,5	-3,4237	0

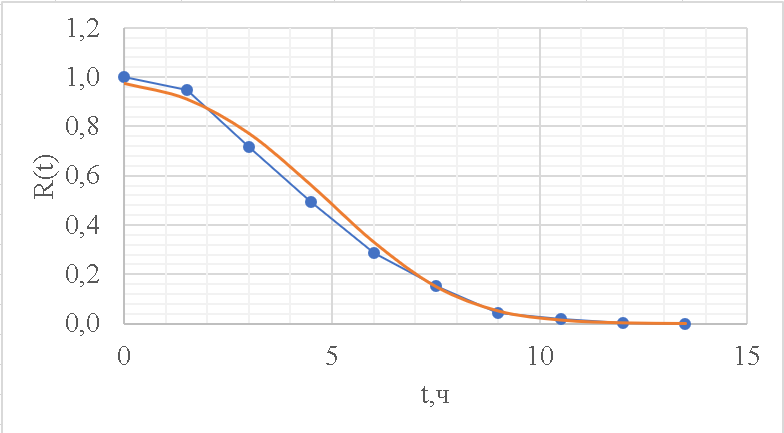
Рисунок 7 - Функция надежности; - ; -







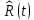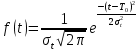
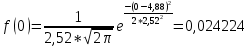
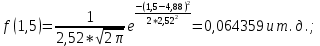
Таблица 9

t
0	0,024224
1,5	0,064359
3	0,119906
4,5	0,156657
6	0,143527
7,5	0,092212
9	0,041545
10,5	0,013126
12	0,002908
13,5	0,000452

---

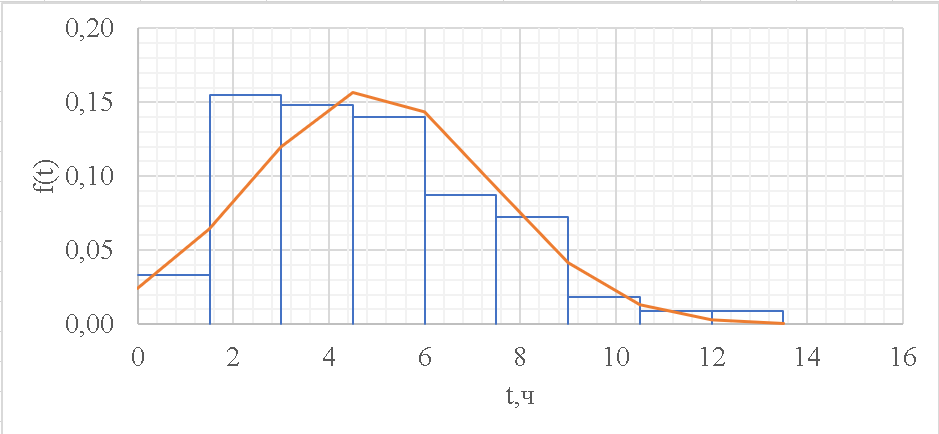
Рисунок 8 - Плотность распределения наработки; - ; -







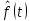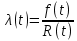
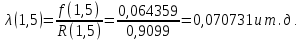
Таблица 10

t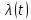
0	0,024891
1,5	0,070731
3	0,155662
4,5	0,279945
6	0,434929
7,5	0,618043
9	0,822669
10,5	0,944287
12	1,118462
13,5	1,505992

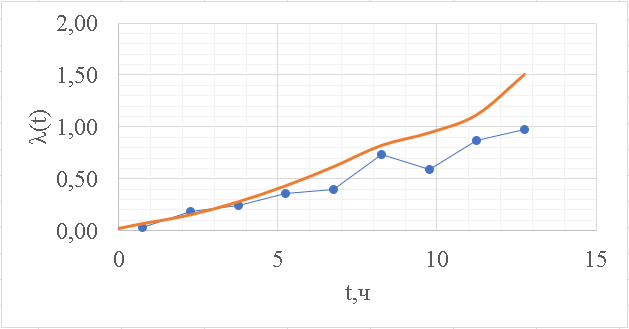
Рисунок 9 - Интенсивность отказов; - ; -

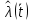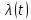
Оценим нормальный закон распределения с помощью критерия согласия Пирсона.

В соответствии с критерием Пирсона, случайная величина



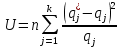
определяющая расхождение между теоретическим законом распределения и имеющимися статистическими данными, подчиняется закону 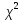распределения с 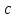степенями свободы. Здесь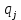

---

– вероятности отказов в соответствующих интервалах. Для нормального распределения







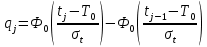
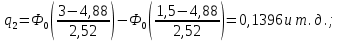
Таблица 7

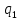	0,0633
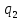	0,1396
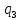	0,2107
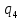	0,2296
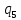	0,1808
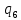	0,0987
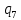	0,0366
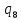	0,0113
	0,0023

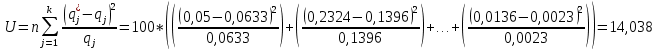
Число степеней свободы , где 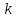– это число интервалов статистического ряда, – число наложенных связей. Для нормального закона 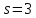, тогда



Используя таблицу квантилей определяем, что вероятность данного распределения 0,025.

Распределение Вейбулла

---

Смотрите также файлы

• Педагог ызметкерлер мен олара теестірілген тлаларды лауазымдарыны лгілік біліктілік сипаттамаларын бекіту туралы.docx

• Институт пра.docx

• Методическая система учителя иностранного языка при подготовке учащихся к итоговой аттестации по английскому языку.docx

• 1. Бег Метание Плавание.docx

• Тесты для оценки степени усвоения дисциплины Продолжите Делопроизводство это Ответ 1 Система хранения документов Ответ 2 Составление документов.docx