ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.01.2024
Просмотров: 153
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
;t)C A = U.
A = U.
Очевидно, что B=B U.Cучетом условия г) В=В
U.Cучетом условия г) В=В  (С
(С  А).
А).
Тогда по доказанному выше (см. пример 2, § 1.3)
В=(В С)
С) (В
(В  А), но с учетом условия
А), но с учетом условия
а) В = (В С)
С)  А = В
А = В  С, т.е. В = В
С, т.е. В = В  С. Поэтому
С. Поэтому
а В=> а
В=> а В и а
В и а С=> В
С=> В (В
(В  С)=>. В
С)=>. В В и В
В и В С.
С.
Очевидно, что B B, отсюда следует, что B
B, отсюда следует, что B C.
C.
В то же время (с учетом условий в), б), а также в соответствии с доказанным выше примером 2 § 1.3):
С = С
U = С (В
(В  А) = (С
А) = (С  В) и (С
В) и (С  А)
А)  (С
(С  В) (С
В) (С В)
В)  Ø = С
Ø = С  В.
В.
Поэтому
а С => а
С => а С и а
С и а  В =>С (С
В =>С (С  В) => С
В) => С  С и С
С и С  В.
В.
Отсюда следует, что С В.
В.
Таким образом, откуда 5 = С. Следовательно, В = С = А и Л - единственно, что и требовалось В С и С
С и С  В, откуда В=С. Следовательно, В=С=А и А – единственно, что и требовалось доказать.
В, откуда В=С. Следовательно, В=С=А и А – единственно, что и требовалось доказать.
Пример 4*. Пусть даны множества А, В, С такие, что А В
В  С= U и A, В, С попарно не пересекаются. Доказать, что
С= U и A, В, С попарно не пересекаются. Доказать, что
А=В С, В=А
С, В=А С,С = А
С,С = А В.
В.
По условию, А, В, С попарно не пересекаются, т.е.
а)А В = Ø; 6)А
В = Ø; 6)А  С=0; в)В
С=0; в)В С=Ø,
С=Ø,
кроме того,
г) А В
В  С = U. т.е А
С = U. т.е А (В
(В  С) = U.
С) = U.
Следовательно, В С удовлетворяет условиям для А , которое единственно (в соответствии с доказанным в примере 3). Поэтому А =В
С удовлетворяет условиям для А , которое единственно (в соответствии с доказанным в примере 3). Поэтому А =В  С, что и требовалось доказать. Аналогично доказывается В= А
С, что и требовалось доказать. Аналогично доказывается В= А С и С = А
С и С = А В
В
Упражнения
Пусть А, В, С
U. Проиллюстрировать на примере конкретных множеств и с помощью диаграмм Венна справедливость следующих соотношений:
2*. Пусть даны множества А, В, С, причем С В. Доказать, что
В. Доказать, что
3*. Доказать эквивалентность приведенных ниже утверждений, т.е. что из каждого следует другое:
A B=U;
B=U; 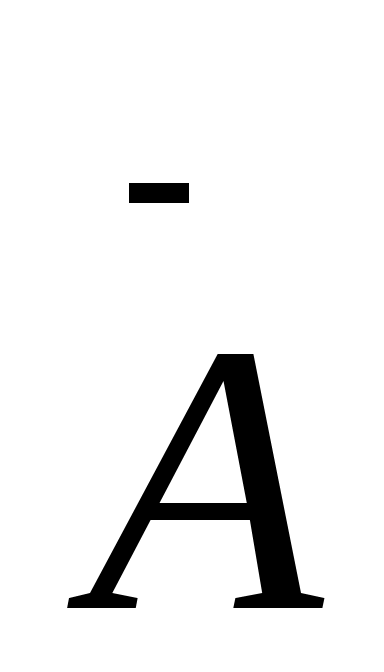
 B;
B; 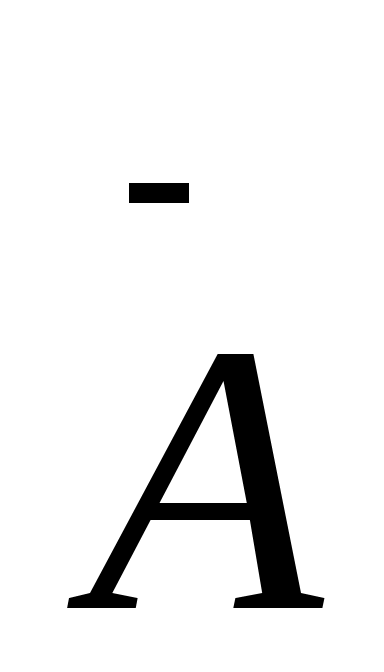

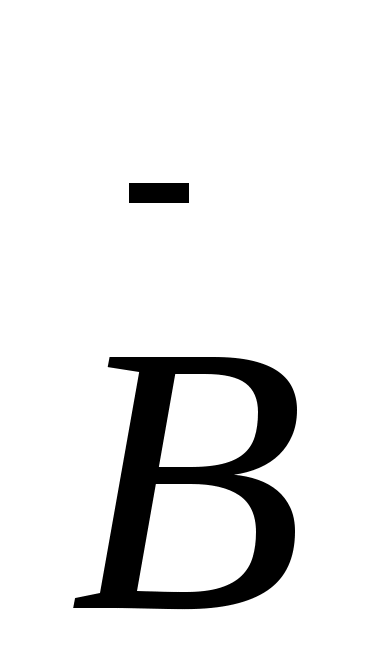 = Ø,.
= Ø,.
Векторы, прямые произведения, проекции векторов
Для описания свойств элементов множества удобны векторные представления. Пусть нас интересуют свойства (значения, состояния, признаки, атрибуты и т. п.) элементов v множества V nфиксированным характеристикам (парамет) А1 А2,... ,Ап; при этом каждая характеристика A. (i=1,2, ..., п) представлена множеством из т . — \А.\допустимых значений а. А. [см. поясняющий пример 1]. В таком случае каждый элемент v множества Сможет быть задан упорядоченным набором значений av а2,..., а по интересуемым характеристикам AVA2,..., Ап, так что а1
А. [см. поясняющий пример 1]. В таком случае каждый элемент v множества Сможет быть задан упорядоченным набором значений av а2,..., а по интересуемым характеристикам AVA2,..., Ап, так что а1  А1, а2
А1, а2 А2,..., ап
А2,..., ап А
А
Очевидно, что B=B
Тогда по доказанному выше (см. пример 2, § 1.3)
В=(В
а) В = (В
а
Очевидно, что B
В то же время (с учетом условий в), б), а также в соответствии с доказанным выше примером 2 § 1.3):
С = С
U = С
Поэтому
а
Отсюда следует, что С
Таким образом, откуда 5 = С. Следовательно, В = С = А и Л - единственно, что и требовалось В
Пример 4*. Пусть даны множества А, В, С такие, что А
А=В
-
Докажем, что A= В С.
С.
По условию, А, В, С попарно не пересекаются, т.е.
а)А
кроме того,
г) А
Следовательно, В
Упражнения
-
Доказать справедливость соотношений:
Пусть А, В, С
U. Проиллюстрировать на примере конкретных множеств и с помощью диаграмм Венна справедливость следующих соотношений:
-
А (В
(В  С) =( А
С) =( А В)
В)  С;
С; -
А (В
(В С) = (А
С) = (А В)
В) С;
С; -
А (А
(А В) = А;
В) = А; -
(А В)
В)  (А
(А ¯В)= А
¯В)= А -
А ( ¯ А
( ¯ А В) = А
В) = А В.
В.
2*. Пусть даны множества А, В, С, причем С
-
А С
С  А
А В;
В; -
А С
С  А
А В;
В; -
А/С А/В;
А/В; -
С/А В/А;
В/А;
3*. Доказать эквивалентность приведенных ниже утверждений, т.е. что из каждого следует другое:
A
Векторы, прямые произведения, проекции векторов
Для описания свойств элементов множества удобны векторные представления. Пусть нас интересуют свойства (значения, состояния, признаки, атрибуты и т. п.) элементов v множества V nфиксированным характеристикам (парамет) А1 А2,... ,Ап; при этом каждая характеристика A. (i=1,2, ..., п) представлена множеством из т . — \А.\допустимых значений а.