ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.01.2024
Просмотров: 273
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– изобарные мольные теплоемкости низкокипящего и высококипящего компонентов в жидких фазах, кДж/кг.
Скрытая теплота парообразования смеси:
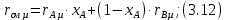
где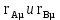 – мольная скрытая теплота парообразования, кДж/кг.
– мольная скрытая теплота парообразования, кДж/кг.
Энтальпия кипящей жидкости:

Энтальпия сухого насыщенного пара:
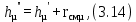
В диапазоне температур кипения чистых компонентов определяют энтальпию кипящей жидкости по формуле (3.13) и энтальпию насыщенного пара по формуле (3.14).
Приведем расчет для температуры 104 оС:
Изобарные мольные теплоемкости низкокипящего и высококипящего компонентов в жидких фазах:
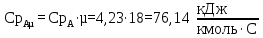
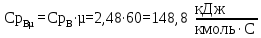
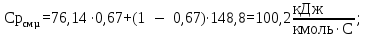
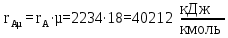
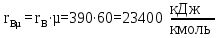
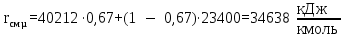
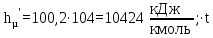
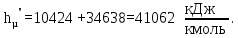
Расчеты для остальных температур выполняем аналогично и сводим в таблицу 3.4.
Таблица 3.4 ‒ Данные для построения диаграммы фазового равновесия h=f(x,y)
Диаграммы фазового равновесия h=f(x,y) представлена на рисунке 3.3.
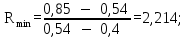
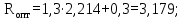
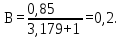
Теоретическое число тарелок в укрепляющей части = 6 шт.
Теоретическое число тарелок в исчерпывающей части =8 шт.
Суммарное число тарелок ‒ 14 шт.
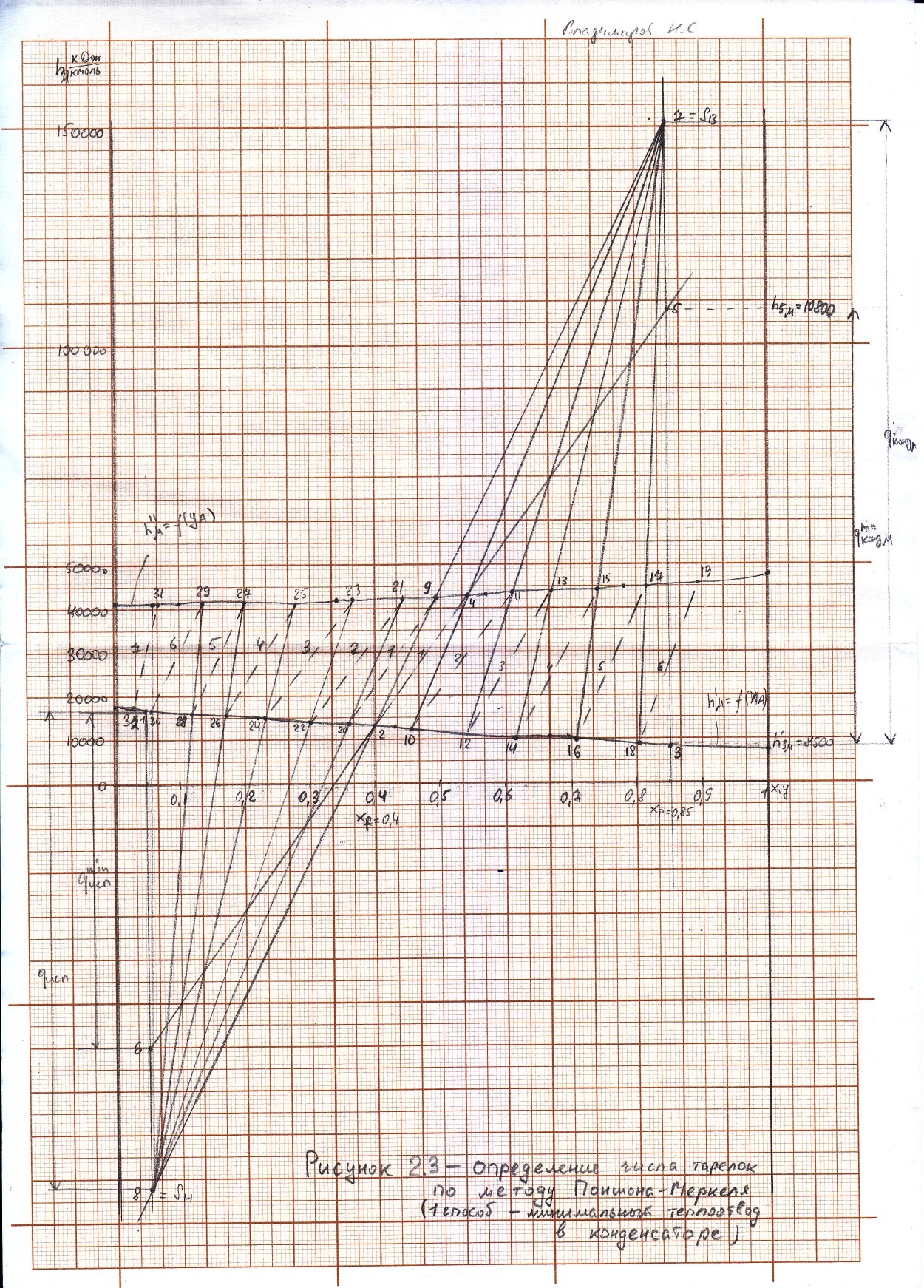
Определение теоретического числа тарелок по методу Поншона – Меркеля производится с помощью энтальпийной диаграммы h ‒ x,y.
В энтальпийной диаграмме необходимо определить теоретическое число тарелок, не используя понятия рабочей линии, т.е иным путем устанавливая связь между сопряженными концентрациями компонента А (НКК) в жидкости и паре. С этой целью необходимо определить положение двух полюсов (Sв; Sн) верхней укрепляющей и нижней отгонной частей колонны, через которые можно проводить лучи, соединяющие точки сопряженных составов газовой и жидкой фаз в любом сечении аппарата.
Верхний полюс колонны определим с помощью минимального теплоотвода в конденсаторе, который определим графически (1 способ), а также удельного теплового потока в конденсаторе, рассчитанного по формуле (2 способ).
Построение энтальпийной диаграммы h ‒ x,y представлено в пункте 3.1.3.
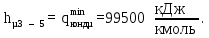
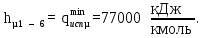
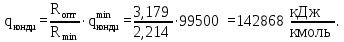
Точка 7 = Sв (верхний полюс):
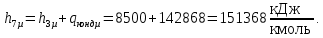
Точка 8 = Sн (нижний полюс): главный луч Sв ‒ т. 2 хw = 0,05;
Далее аналогично пока x< хР=0,85
Далее аналогично пока x> хw=0,05
Таким образом число тарелок по методу Поншона ‒ Меркеля: в укрепляющей части колонны ‒ 6 тарелок, в исчерпывающей части колонны – 7 тарелок.
Суммарное число тарелок ‒ 13 шт.
Построение диаграммы и выполнение первых шагов построения аналогично предыдущему способу.
Определяется удельный тепловой поток в конденсаторе по формуле:
где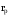 ‒ скрытая теплота фазового перехода дистиллята.
‒ скрытая теплота фазового перехода дистиллята.
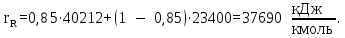
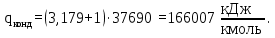
Процесс построения методом изотерм аналогичен предыдущему способу.
Таким образом, число тарелок по методу Поншона ‒ Меркеля (2 способ): в укрепляющей части колонны – 6 тарелки, в исчерпывающей части колонны – 6 тарелок.
В дальнейшем для расчетов принимаем число тарелок в укрепляющей части колонны ‒ 6 тарелок, в исчерпывающей части колонны – 8 тарелок. Суммарное число тарелок ‒ 14 шт.
Количество реальных (действительных) тарелок:
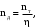 (3.20)
(3.20)
где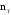 ‒ теоретическое число тарелок;
‒ теоретическое число тарелок;
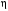 ‒ КПД контактного устройства, принимаем
‒ КПД контактного устройства, принимаем 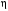 = 0,8.
= 0,8.
Тогда действительное число тарелок в укрепляющей части колонны:
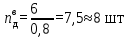
Действительное число тарелок в исчерпывающей части колонны:
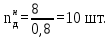
Общее число тарелок в колонне – 18 штук.
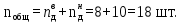
Скрытая теплота парообразования смеси:
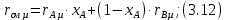
где
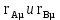 – мольная скрытая теплота парообразования, кДж/кг.
– мольная скрытая теплота парообразования, кДж/кг. Энтальпия кипящей жидкости:

Энтальпия сухого насыщенного пара:
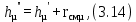
В диапазоне температур кипения чистых компонентов определяют энтальпию кипящей жидкости по формуле (3.13) и энтальпию насыщенного пара по формуле (3.14).
Приведем расчет для температуры 104 оС:
Изобарные мольные теплоемкости низкокипящего и высококипящего компонентов в жидких фазах:
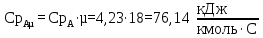
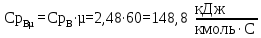
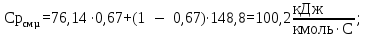
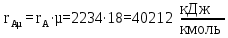
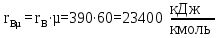
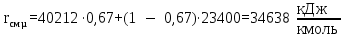
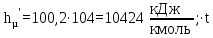
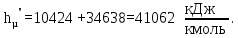
Расчеты для остальных температур выполняем аналогично и сводим в таблицу 3.4.
Таблица 3.4 ‒ Данные для построения диаграммы фазового равновесия h=f(x,y)
| t, оС | 100 | 104 | 108 | 112 | 116 | 118,1 |
| Ра, кПа | 100,0 | 117,3 | 134,7 | 154,2 | 175,9 | 188,3 |
| Рв, кПа | 56,9 | 65,1 | 74,2 | 84,4 | 95,7 | 100,0 |
| ха | 1,00 | 0,67 | 0,43 | 0,22 | 0,05 | 0,00 |
| уа | 1,00 | 0,78 | 0,57 | 0,34 | 0,09 | 0,00 |
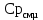 , кДж/(кмоль·К) , кДж/(кмоль·К) | 76,1 | 100,2 | 117,8 | 132,6 | 144,9 | 148,8 |
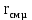 , кДж/кмоль , кДж/кмоль | 40212 | 34638 | 30563 | 27158 | 24305 | 23400 |
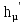 , кДж/кмоль , кДж/кмоль | 7614 | 10424 | 12727 | 14847 | 16807 | 17573 |
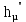 , кДж/кмоль , кДж/кмоль | 47826 | 45062 | 43290 | 42005 | 41112 | 40973 |
Диаграммы фазового равновесия h=f(x,y) представлена на рисунке 3.3.
3.1.4 Графический метод определения теоретического числа тарелок методом Мак ‒ Кэба ‒ Тиле
-
Строим диаграмму фазового равновесия y=f(x). -
Построение точки а. XР = 0,85 пересекаем с главной диагональю. -
Построение точки с. Xw = 0,05 пересекаем с главной диагональю. -
Построение точки d. На оси ординат от «0» откладываем значение отрезка В, который рассчитывается по формуле:
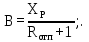 где 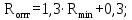 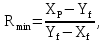 где 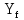 определяем подиаграмме фазового равновесия определяем подиаграмме фазового равновесияy=f(x=0,4). 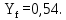 | (3.15) (3.16) (3.17) |
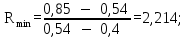
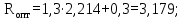
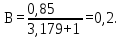
-
Через точку а и точку d проводим рабочую линию укрепляющей части колонны. Получаем отрезок аd. -
На эту рабочую линию выносим значение концентрации НКК Xf=0,4 в исходной смеси. Получаем точку в. Эта точка характеризует концентрацию НКК на питательной тарелке. Так как питательная тарелка разделяет укрепляющую и исчерпывающую части колонны, то здесь заканчивается укрепляющая часть и с нее начинается исчерпывающая часть. -
Через точку с в точку в проводим рабочую линию исчерпывающей части колонны. -
Построив рабочие линии, можно приступить к изображению процессов фазовых переходов, проходящих в жидкой фазе на тарелках. Очерчиваем область, лежащую между рабочими линиями abc и кривой равновесия. -
Находим теоретическое число тарелок, строя ступени в рабочей области из точки а в точку с. -
Количество таких ступеней до точки в определяет число теоретических тарелок в укрепляющей части колонны. Аналогичные построения от точки в до точки с дают число теоретических тарелок в исчерпывающей части колонны.
Теоретическое число тарелок в укрепляющей части = 6 шт.
Теоретическое число тарелок в исчерпывающей части =8 шт.
Суммарное число тарелок ‒ 14 шт.
3.1.5 Графический метод Поншона ‒ Меркеля в координатах h ‒ x,y.
Определение теоретического числа тарелок по методу Поншона – Меркеля производится с помощью энтальпийной диаграммы h ‒ x,y.
В энтальпийной диаграмме необходимо определить теоретическое число тарелок, не используя понятия рабочей линии, т.е иным путем устанавливая связь между сопряженными концентрациями компонента А (НКК) в жидкости и паре. С этой целью необходимо определить положение двух полюсов (Sв; Sн) верхней укрепляющей и нижней отгонной частей колонны, через которые можно проводить лучи, соединяющие точки сопряженных составов газовой и жидкой фаз в любом сечении аппарата.
Верхний полюс колонны определим с помощью минимального теплоотвода в конденсаторе, который определим графически (1 способ), а также удельного теплового потока в конденсаторе, рассчитанного по формуле (2 способ).
Построение энтальпийной диаграммы h ‒ x,y представлено в пункте 3.1.3.
-
Отмечаем т.1 ‒ точку пересечения линии h’ и хw =0,05; -
Отмечаем т.2 ‒ точку пересечения линии h’ и хf =0,4; -
Отмечаем т.3 ‒ точку пересечения линии h’ и хР=0,85; -
Отмечаем т.4 на линии h’’(уа); по хf =0,4 на диаграмме y=f(x) находим уf =0,54. -
Проводим изотерму через точки 2 и 4. Получаем точки 5 и 6. Отрезок 5 ‒ 6 – вспомогательный луч. -
Определим qконд и qисп:
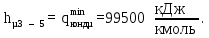
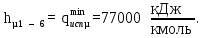
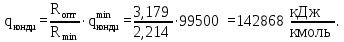
-
Определяем положение верхнего и нижнего полюса:
Точка 7 = Sв (верхний полюс):
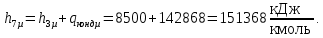
Точка 8 = Sн (нижний полюс): главный луч Sв ‒ т. 2 хw = 0,05;
-
Точка 9. Главный луч Sв ‒ Sн h’’. -
Точка 10. Луч Sв ‒ 4 пересекает h’. -
По х10 определяем у11 (по диаграмме t,x,y).
Далее аналогично пока x< хР=0,85
-
Главный луч SвSн пересекает h’’ в точке 9. -
По у9 определяем х20 (по диаграмме t,x,y). -
Точка 21. х20 пересекает h’.
Далее аналогично пока x> хw=0,05
Таким образом число тарелок по методу Поншона ‒ Меркеля: в укрепляющей части колонны ‒ 6 тарелок, в исчерпывающей части колонны – 7 тарелок.
Суммарное число тарелок ‒ 13 шт.

3.1.6. Метод с расчётом удельного теплового потока в конденсаторе
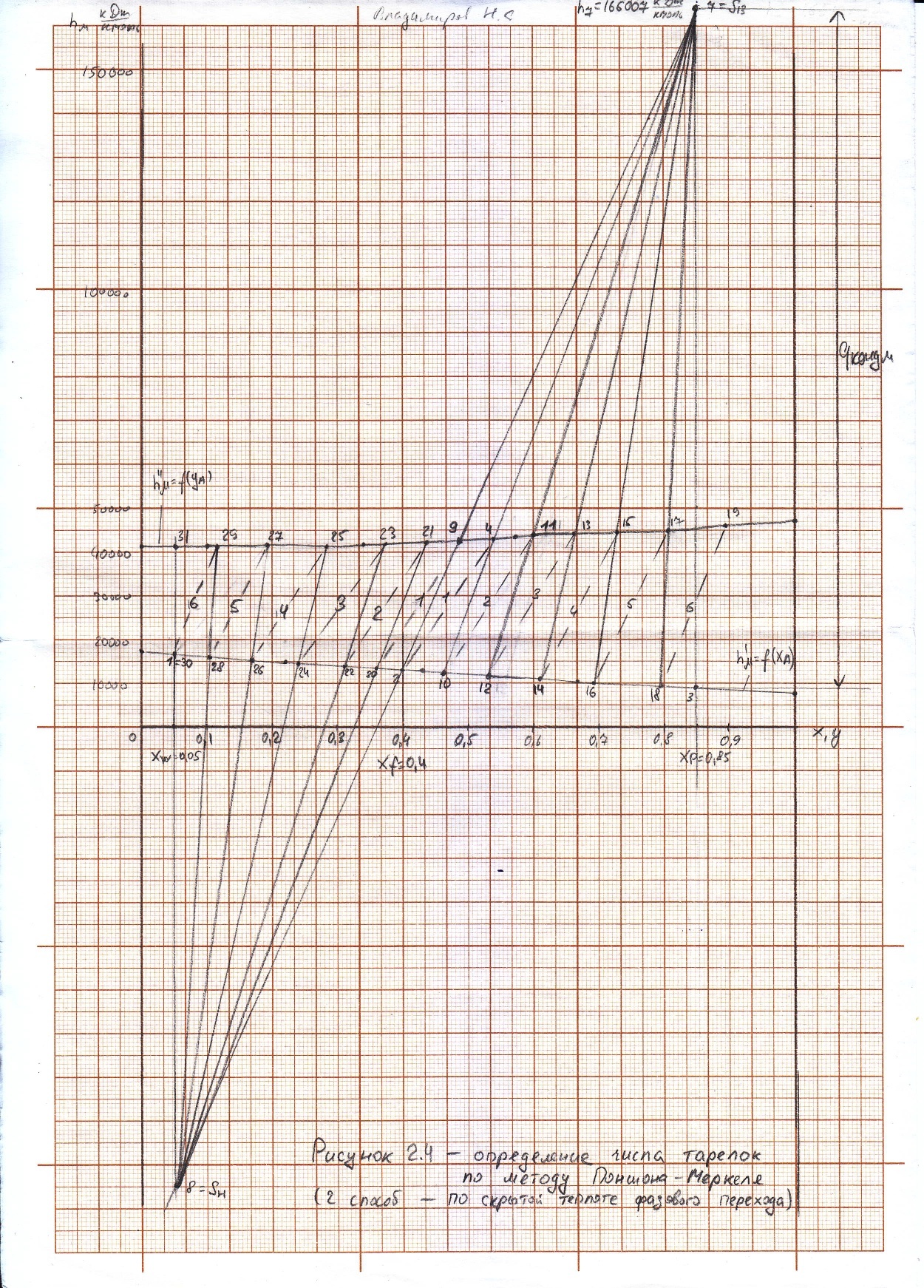
Построение диаграммы и выполнение первых шагов построения аналогично предыдущему способу.
Определяется удельный тепловой поток в конденсаторе по формуле:
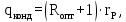 | (3.18) |
где
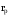 ‒ скрытая теплота фазового перехода дистиллята.
‒ скрытая теплота фазового перехода дистиллята. 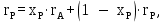 | (3.19) |
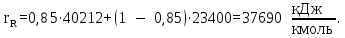
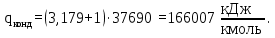
Процесс построения методом изотерм аналогичен предыдущему способу.
Таким образом, число тарелок по методу Поншона ‒ Меркеля (2 способ): в укрепляющей части колонны – 6 тарелки, в исчерпывающей части колонны – 6 тарелок.
В дальнейшем для расчетов принимаем число тарелок в укрепляющей части колонны ‒ 6 тарелок, в исчерпывающей части колонны – 8 тарелок. Суммарное число тарелок ‒ 14 шт.

3.1.7. Определение действительного числа тарелок
Количество реальных (действительных) тарелок:
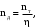 (3.20)
(3.20)где
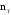 ‒ теоретическое число тарелок;
‒ теоретическое число тарелок;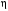 ‒ КПД контактного устройства, принимаем
‒ КПД контактного устройства, принимаем 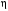 = 0,8.
= 0,8.Тогда действительное число тарелок в укрепляющей части колонны:
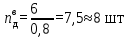
Действительное число тарелок в исчерпывающей части колонны:
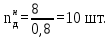
Общее число тарелок в колонне – 18 штук.