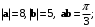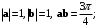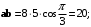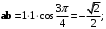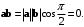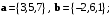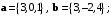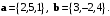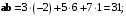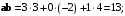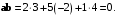ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.01.2024
Просмотров: 46
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема 7. Евклидово векторное пространство
-
Скалярное произведение. -
Аксиомы скалярного произведения. -
Евклидовы пространства. -
Длина вектора и угол между векторами. -
Неравенство Коши - Буняковского - Шварца. -
Неравенство треугольника. -
Ортогональные векторы и теорема Пифагора. -
Метрическая форма и метрические коэффициенты. -
Формулы преобразования метрических коэффициентов при замене базиса.
-
Скалярное произведение.
Определение 7.1. Углом
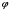 между векторами
между векторами 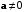 и
и 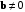 называется наименьший угол между этими векторами, приведенными к общему началу. Его обозначение
называется наименьший угол между этими векторами, приведенными к общему началу. Его обозначение 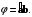 Очевидно, что
Очевидно, что 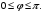
Определение 7.2. Скалярным произведением двух векторов
 и
и 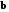 называется число, равное произведению длин этих векторов на косинус угла между ними (рис. 7.1)
называется число, равное произведению длин этих векторов на косинус угла между ними (рис. 7.1)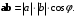 (7.1)
(7.1)Таким образом, скалярное произведение двух векторов равно длине одного из них, умноженной на проекцию второго вектора на ось, направление которой определяется первым вектором.
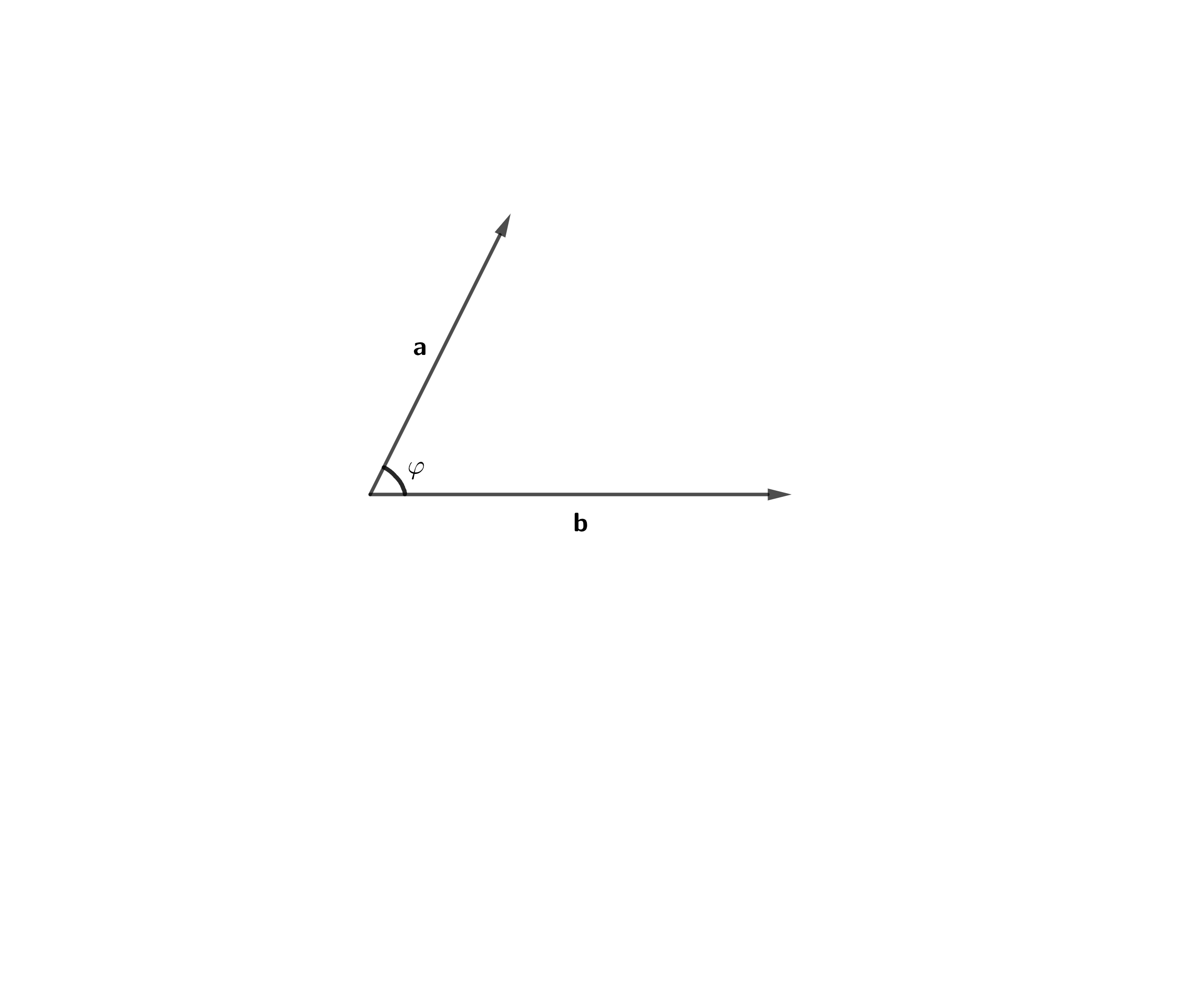
Рисунок 7.1 – Скалярное произведение векторов
 и
и 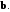
Определение 7.3. Проекциями вектора
 на координатные оси
на координатные оси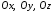 называют координаты вектора:
называют координаты вектора: 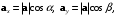
 (7.2)
(7.2)где
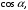
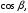
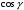 – направляющие косинусы вектора;
– направляющие косинусы вектора; 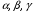 – углы между вектором
– углы между вектором  и осями координат
и осями координат 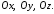
Для направляющих косинусов выполняется равенство:
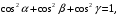
где
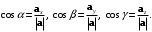
Определение7.4. Проекцией вектора
 на вектор
на вектор  называется число
называется число 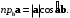
Пример7.1.Найти скалярное произведение векторов
 и
и  в каждом из следующих случаев:
в каждом из следующих случаев: Решение. По определению скалярного произведения (7.1) имеем:
Пример7.2. Вычислить скалярное произведение векторов
 и
и 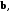 заданных координатами
заданных координатамиРешение. Подразумеваем, что координаты векторов даны в ортонормированном базисе. Если
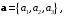
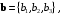 то в ортонормированном базисе
то в ортонормированном базисе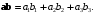
Имеем
-
Аксиомы скалярного произведения.
Пусть
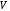 – произвольное линейное пространство над полем
– произвольное линейное пространство над полем 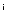 вещественных чисел.
вещественных чисел.Определение7.5 Скалярным произведением на пространстве
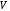 называется произвольная функция
называется произвольная функция 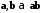 (7.3)
(7.3)пары векторов, принимающая числовые значения.
Скалярное произведение обладает следующими свойствами:
 Коммутативность. Для любых векторов
Коммутативность. Для любых векторов 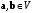
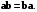
 Ассоциативность. Для любых векторов
Ассоциативность. Для любых векторов 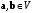 и любого числа
и любого числа 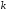
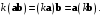
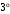 Дистрибутивность. Для любых векторов
Дистрибутивность. Для любых векторов 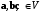
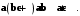
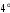 Положительность. Для любого отличного от нуля вектора
Положительность. Для любого отличного от нуля вектора 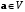
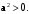
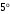
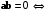
 прямой угол;
прямой угол; 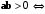
 острый угол;
острый угол; 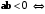
 тупой угол.
тупой угол.Пример 7.3. В координатах даны векторы:
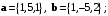
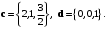
Вычислить скалярные произведения всех пар данных векторов. Какой угол образуют эти пары векторов?
Решение. Вычислять будем путём сложения произведений соответствующих координат.
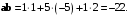
Получили отрицательное число, поэтому векторы образуют тупой угол.
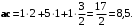
Получили положительное число, поэтому векторы образуют острый угол.
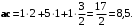
Получили положительное число, поэтому векторы образуют острый угол.
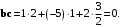
Получили нуль, поэтому векторы образуют прямой угол.
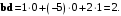
Получили положительное число, поэтому векторы образуют острый угол.
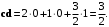
Получили положительное число, поэтому векторы образуют острый угол.
-
Евклидовы пространства.
Определение 7.6. Линейное пространство
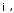 для которого выбрано и зафиксировано некоторое скалярное произведение (7.2), называется евклидовым линейным пространством.
для которого выбрано и зафиксировано некоторое скалярное произведение (7.2), называется евклидовым линейным пространством.Линейное векторное пространство обладает свойствами скалярного произведения 1-5.
Теорема 7.1. Скалярное произведение в евклидовом пространстве есть положительно определенная симметричная билинейная функция. И наоборот, любую положительно определенную симметричную функцию можно выбрать в качестве скалярного произведения.
-
Длина вектора и угол между векторами.
Определение 7.7. Длина вектора
 определяется формулой
определяется формулой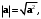 (7.4)
(7.4)а угол между отличными от нуля векторами
 и
и  – формулами
– формулами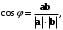 (7.5)
(7.5)которая дает для
 два значения, в сумме составляющие
два значения, в сумме составляющие 
Пример. Дан вектор
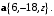 Найти
Найти 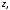 если
если 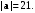
Решение. В силу (7.4) имеем
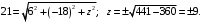
Пример 7.4. Найти угол
 между векторами
между векторами 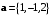 и
и 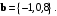
Решение. Применим формулу (7.5):
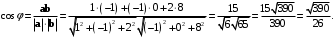
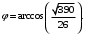
-
Неравенство Коши - Буняковского - Шварца.
В евклидовом точечном пространстве расстояние
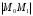 между двумя точками определяется формулой
между двумя точками определяется формулой 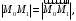
а угол
 между двумя прямыми – формулой (7.5), в которой
между двумя прямыми – формулой (7.5), в которой  и
и  – произвольные направляющие векторы данных прямых.
– произвольные направляющие векторы данных прямых.Аксиома положительности означает, что для любого вектора
 формула (7.4) однозначно определяет длину
формула (7.4) однозначно определяет длину 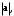 являющуюся неотрицательным числом. При этом
являющуюся неотрицательным числом. При этом 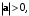 если
если 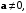 и
и 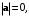 если
если 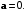
В формуле (7.5) правая часть принадлежит области определения арккосинуса, т.е. число
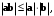
или
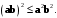 (7.6)
(7.6)Это неравенство называется неравенством Коши-Буняковского-Шварца.
Для доказательства рассмотрим функцию
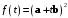
числовой переменной
 Согласна аксиоме 4 для всех
Согласна аксиоме 4 для всех  имеет место неравенство
имеет место неравенство 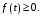 С другой стороны,
С другой стороны, 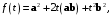
а из элементарной алгебры известно