ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.01.2024
Просмотров: 48
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, что если квадратный трехчлен принимает лишь неотрицательные значения, то его дискриминант неположителен. В данном случае дискриминант равен
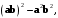
что и доказывает неравенство (7.6).
Если векторы и
и  коллинеарны, то в (7.6) имеет место равенство. Обратно, если
коллинеарны, то в (7.6) имеет место равенство. Обратно, если 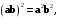 то при
то при 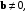 согласно формуле для корней квадратного уравнения,
согласно формуле для корней квадратного уравнения, 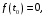 где
где 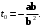 Поэтому
Поэтому 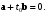
Таким образом, неравенство Коши-Буняковского-Шварца обращается в равенство для коллинеарных векторов и
и 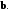
Пример 7.5. Докажите неравенство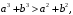 если
если 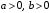 и
и 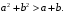
Доказательство. Домножим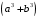 на
на 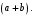 Имеем
Имеем
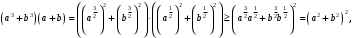 Воспользуемся неравенством Коши-Буняковского для векторов с координатами:
Воспользуемся неравенством Коши-Буняковского для векторов с координатами: 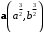 и
и 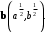
Теперь поскольку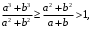 то
то 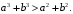
Из неравенств Коши-Буняковского следует, что
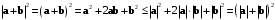
и, аналогично, что
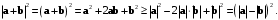
Отсюда следует, что
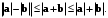 (7.7)
(7.7)
Если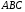 – произвольный треугольник и
– произвольный треугольник и 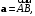
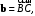
то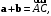 и получаем из (7.7) неравенства:
и получаем из (7.7) неравенства:
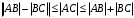
(сторона треугольника не больше суммы двух других сторон и не меньше их разности). На этом основании неравенства (7.7) называются неравенствами треугольника.
Пример 7.6. Внутри треугольника взята точка
взята точка 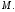 (рис. 7.2). Доказать, что периметр треугольника
(рис. 7.2). Доказать, что периметр треугольника 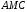 меньше периметра треугольника
меньше периметра треугольника 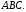
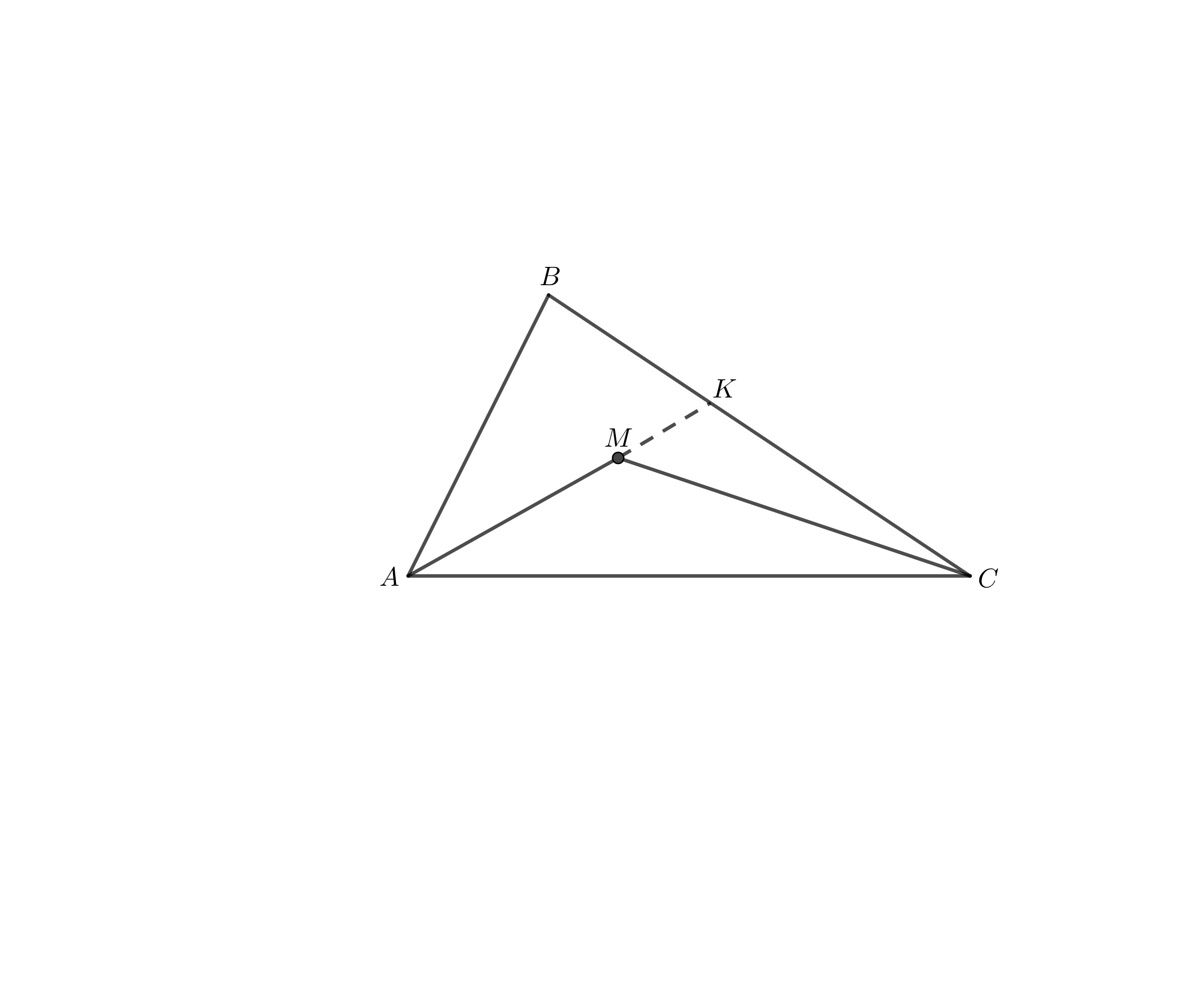
Рисунок 7.2 – Треугольник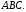
Доказательство. Так как у треугольников и
и 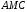 сторона
сторона 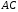 – общая, то достаточно доказать, что
– общая, то достаточно доказать, что 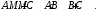
Продлим сторону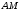 до пересечения со стороной
до пересечения со стороной 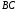 в точке
в точке 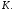 Из
Из 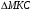 по неравенству треугольника
по неравенству треугольника 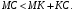 Тогда
Тогда
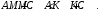 (*).
(*).
Из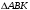 по неравенству треугольника
по неравенству треугольника 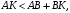 значит,
значит,
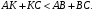 (**).
(**).
Из неравенств (*) и (**) следует, что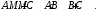 Утверждение доказано.
Утверждение доказано.
Определение 7.8.
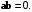
При и
и 
это равносильно тому, что угол между векторами и
и  равен
равен 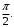
Если векторы и
и  ортогональны, то
ортогональны, то
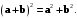 (7.8)
(7.8)
При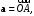
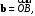 когда
когда 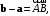 отсюда получаем теорему Пифагора:
отсюда получаем теорему Пифагора:
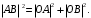
На этом основании равенство (7.8) также называется теоремой Пифагора (рис 7.3).
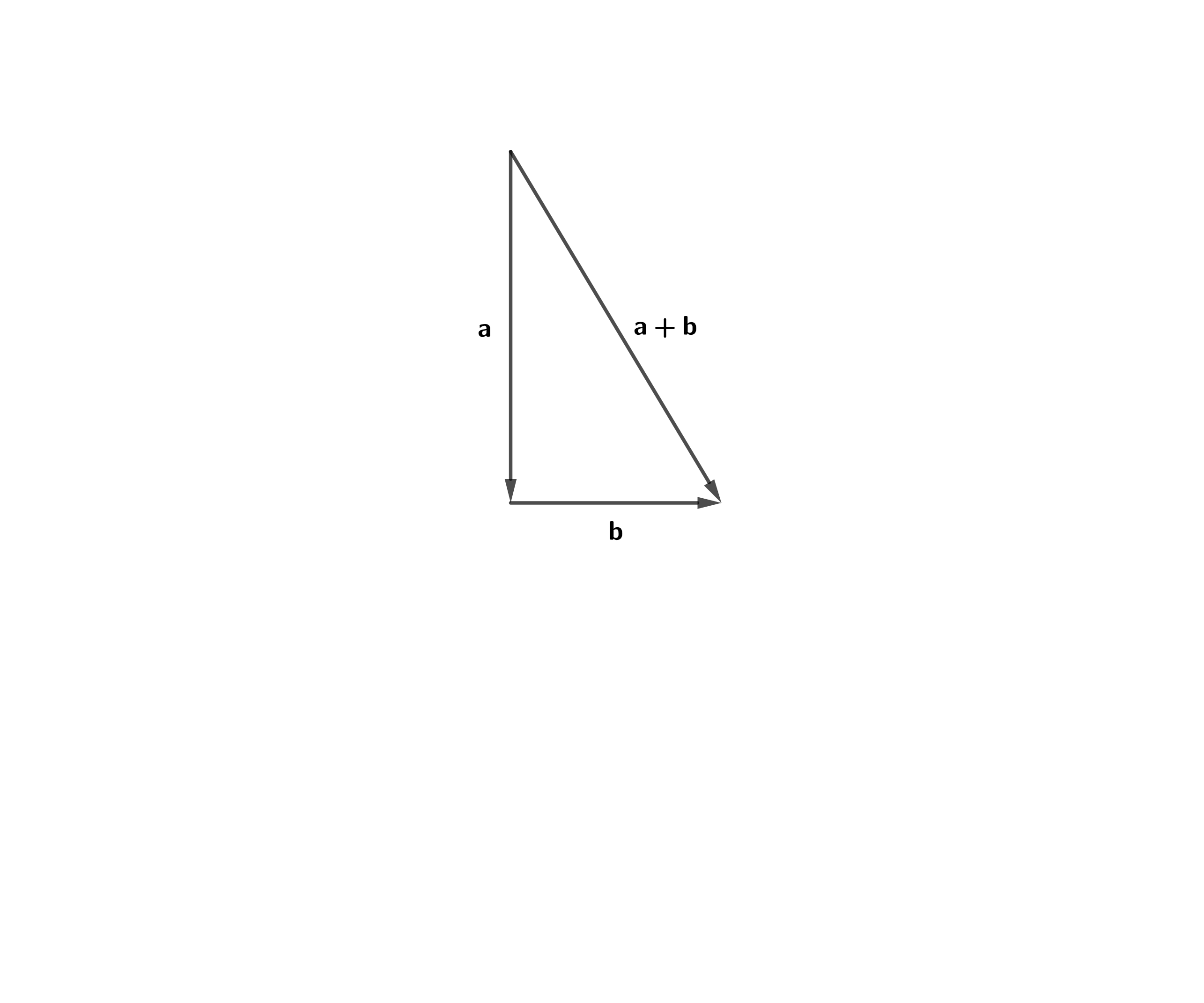
Рисунок 7.3 – Теорема Пифагора.
Пример 7.7. Доказать, что векторы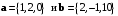 являются ортогональными.
являются ортогональными.
Доказательство. Находим скалярное произведение данных векторов:
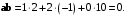
Поскольку произведение векторов равняется нулю, то они являются ортогональными.
Пример 7.8. Найти значение числа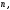 при котором векторы
при котором векторы 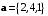 и
и 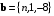 будут являться ортогональными.
будут являться ортогональными.
Решение. Найдем скалярное произведение векторов:
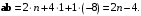
Полученное приравняем к нулю:
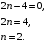
Таким образом, векторы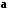 и
и  ортогональны при значении
ортогональны при значении 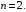
Пусть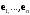 – произвольный базис евклидова линейного пространства
– произвольный базис евклидова линейного пространства 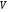 и пусть
и пусть
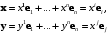
два произвольных вектора этого пространства.
В обозначениях Энштейна
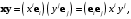
т. е.
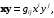 (7.9)
(7.9)
где положено
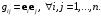 (7.10)
(7.10)
Заметим, что
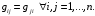 (7.11)
(7.11)
При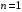 формула (7.9) имеет вид
формула (7.9) имеет вид
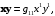
где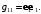
При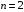 – вид
– вид
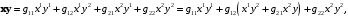
где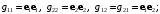
при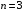 – вид
– вид
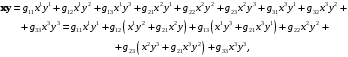
где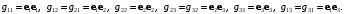
В общем случае запишем подобные члены:
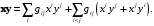
Формулу (7.9) можно записать матричных обозначениях. Пусть
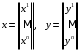
и пусть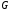 – квадратная
– квадратная  -матрица
-матрица
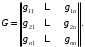 (7.12)
(7.12)
Рассмотрим матрицу
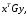
где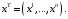 По правилу умножения прямоугольных матриц эта матрица имеет размер
По правилу умножения прямоугольных матриц эта матрица имеет размер 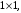 т.е. представляет собой число. Вычислив его, имеем
т.е. представляет собой число. Вычислив его, имеем
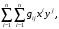 (7.13)
(7.13)
т.е. равно (7.9). Тем самым доказано, что
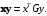 (7.14)
(7.14)
При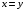 получаем, что
получаем, что
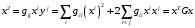 (7.15)
(7.15)
и, в частности, при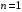
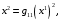
при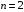
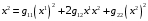
и при
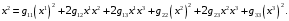
Стоящее в правой части формулы (7.9) алгебраическое выражение представляет собой однородный многочлен от двух наборов переменных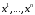 и
и 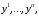 линейный по каждому из этих наборов. Однородные многочлены называют формами, а многочлены вида (7.13) – билинейными формами. Формы (7.13), коэффициенты которых обладают свойством (7.11), называются симметричными формами.
линейный по каждому из этих наборов. Однородные многочлены называют формами, а многочлены вида (7.13) – билинейными формами. Формы (7.13), коэффициенты которых обладают свойством (7.11), называются симметричными формами.
При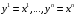 симметричная билинейная форма превращается в однородный многочлен второй степени от переменных
симметричная билинейная форма превращается в однородный многочлен второй степени от переменных 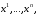 т.е. в квадратичную форму. Согласно аксиоме 4 форма (7.15) обладает тем же свойством, что и
т.е. в квадратичную форму. Согласно аксиоме 4 форма (7.15) обладает тем же свойством, что и
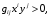
если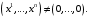 Такие квадратичные формы называются положительно определенными.
Такие квадратичные формы называются положительно определенными.
Таким образом, формула (7.9) утверждает, что скалярное произведение двух векторов является билинейной, симметричной и положительно определенной формой от их координат.
Определение 7.9. Форма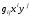 называется метрической формой данного базиса
называется метрической формой данного базиса 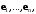 а ее коэффициенты
а ее коэффициенты 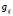 – коэффициентами этого базиса.
– коэффициентами этого базиса.
Пример 7.9. Система координат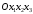 задается репером
задается репером 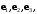 базис которого характеризуется метрическими коэффициентами, составляющими матрицу Грамма
базис которого характеризуется метрическими коэффициентами, составляющими матрицу Грамма
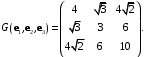
Найти длины базисных векторов и угол между ними.
Решение. Длины базисных векторов находятся из диагональных метрических коэффициентов:
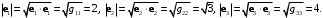
Далее
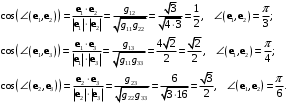
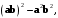
что и доказывает неравенство (7.6).
Если векторы
 и
и  коллинеарны, то в (7.6) имеет место равенство. Обратно, если
коллинеарны, то в (7.6) имеет место равенство. Обратно, если 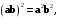 то при
то при 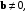 согласно формуле для корней квадратного уравнения,
согласно формуле для корней квадратного уравнения, 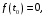 где
где 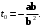 Поэтому
Поэтому 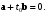
Таким образом, неравенство Коши-Буняковского-Шварца обращается в равенство для коллинеарных векторов
 и
и 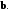
Пример 7.5. Докажите неравенство
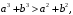 если
если 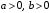 и
и 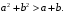
Доказательство. Домножим
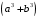 на
на 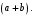 Имеем
Имеем 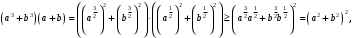 Воспользуемся неравенством Коши-Буняковского для векторов с координатами:
Воспользуемся неравенством Коши-Буняковского для векторов с координатами: 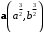 и
и 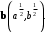
Теперь поскольку
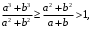 то
то 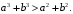
-
Неравенство треугольника
Из неравенств Коши-Буняковского следует, что
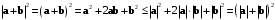
и, аналогично, что
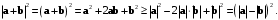
Отсюда следует, что
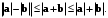 (7.7)
(7.7)Если
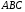 – произвольный треугольник и
– произвольный треугольник и 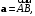
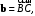
то
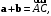 и получаем из (7.7) неравенства:
и получаем из (7.7) неравенства: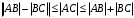
(сторона треугольника не больше суммы двух других сторон и не меньше их разности). На этом основании неравенства (7.7) называются неравенствами треугольника.
Пример 7.6. Внутри треугольника
 взята точка
взята точка 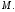 (рис. 7.2). Доказать, что периметр треугольника
(рис. 7.2). Доказать, что периметр треугольника 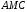 меньше периметра треугольника
меньше периметра треугольника 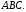

Рисунок 7.2 – Треугольник
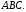
Доказательство. Так как у треугольников
 и
и 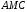 сторона
сторона 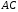 – общая, то достаточно доказать, что
– общая, то достаточно доказать, что 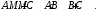
Продлим сторону
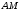 до пересечения со стороной
до пересечения со стороной 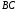 в точке
в точке 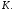 Из
Из 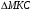 по неравенству треугольника
по неравенству треугольника 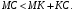 Тогда
Тогда 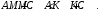 (*).
(*).Из
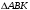 по неравенству треугольника
по неравенству треугольника 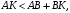 значит,
значит, 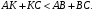 (**).
(**). Из неравенств (*) и (**) следует, что
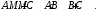 Утверждение доказано.
Утверждение доказано.-
Ортогональные векторы и теорема Пифагора.
Определение 7.8.

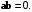
При
 и
и 
это равносильно тому, что угол между векторами
 и
и  равен
равен 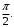
Если векторы
 и
и  ортогональны, то
ортогональны, то 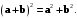 (7.8)
(7.8)При
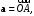
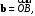 когда
когда 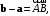 отсюда получаем теорему Пифагора:
отсюда получаем теорему Пифагора: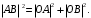
На этом основании равенство (7.8) также называется теоремой Пифагора (рис 7.3).
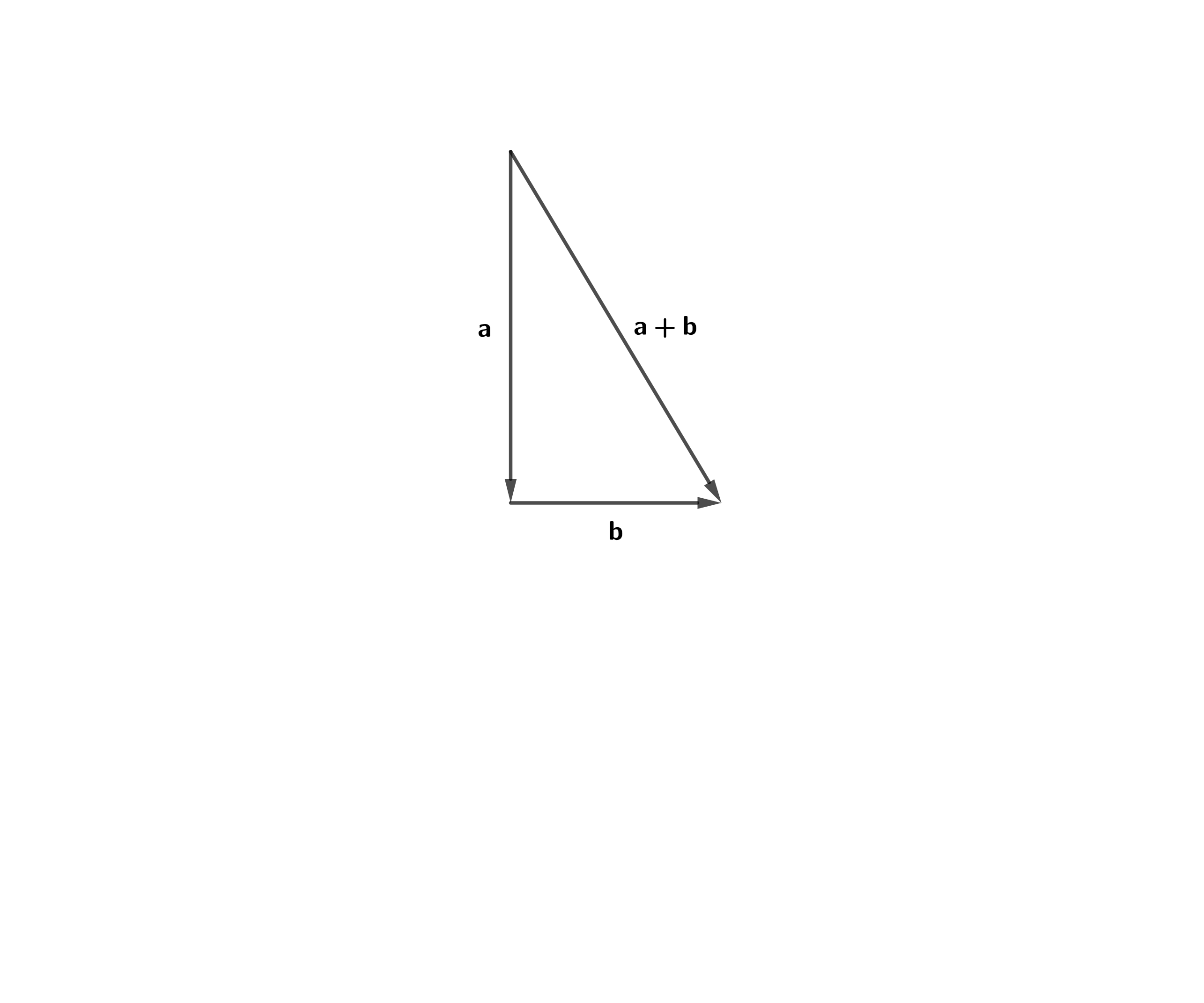
Рисунок 7.3 – Теорема Пифагора.
Пример 7.7. Доказать, что векторы
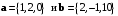 являются ортогональными.
являются ортогональными. Доказательство. Находим скалярное произведение данных векторов:
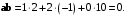
Поскольку произведение векторов равняется нулю, то они являются ортогональными.
Пример 7.8. Найти значение числа
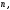 при котором векторы
при котором векторы 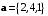 и
и 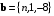 будут являться ортогональными.
будут являться ортогональными.Решение. Найдем скалярное произведение векторов:
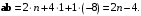
Полученное приравняем к нулю:
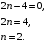
Таким образом, векторы
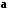 и
и  ортогональны при значении
ортогональны при значении 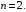
-
Метрическая форма и метрические коэффициенты
Пусть
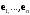 – произвольный базис евклидова линейного пространства
– произвольный базис евклидова линейного пространства 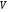 и пусть
и пусть
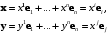
два произвольных вектора этого пространства.
В обозначениях Энштейна
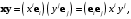
т. е.
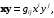 (7.9)
(7.9)где положено
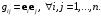 (7.10)
(7.10)Заметим, что
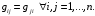 (7.11)
(7.11)При
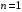 формула (7.9) имеет вид
формула (7.9) имеет вид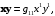
где
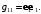
При
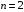 – вид
– вид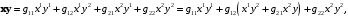
где
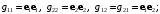
при
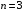 – вид
– вид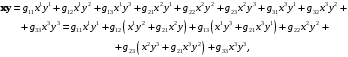
где
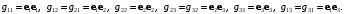
В общем случае запишем подобные члены:
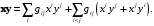
Формулу (7.9) можно записать матричных обозначениях. Пусть
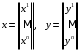
и пусть
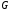 – квадратная
– квадратная  -матрица
-матрица 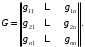 (7.12)
(7.12)Рассмотрим матрицу
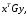
где
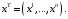 По правилу умножения прямоугольных матриц эта матрица имеет размер
По правилу умножения прямоугольных матриц эта матрица имеет размер 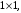 т.е. представляет собой число. Вычислив его, имеем
т.е. представляет собой число. Вычислив его, имеем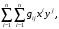 (7.13)
(7.13)т.е. равно (7.9). Тем самым доказано, что
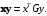 (7.14)
(7.14)При
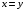 получаем, что
получаем, что 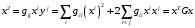 (7.15)
(7.15)и, в частности, при
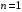
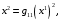
при
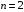
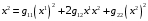
и при

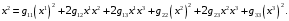
Стоящее в правой части формулы (7.9) алгебраическое выражение представляет собой однородный многочлен от двух наборов переменных
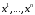 и
и 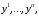 линейный по каждому из этих наборов. Однородные многочлены называют формами, а многочлены вида (7.13) – билинейными формами. Формы (7.13), коэффициенты которых обладают свойством (7.11), называются симметричными формами.
линейный по каждому из этих наборов. Однородные многочлены называют формами, а многочлены вида (7.13) – билинейными формами. Формы (7.13), коэффициенты которых обладают свойством (7.11), называются симметричными формами.При
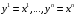 симметричная билинейная форма превращается в однородный многочлен второй степени от переменных
симметричная билинейная форма превращается в однородный многочлен второй степени от переменных 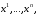 т.е. в квадратичную форму. Согласно аксиоме 4 форма (7.15) обладает тем же свойством, что и
т.е. в квадратичную форму. Согласно аксиоме 4 форма (7.15) обладает тем же свойством, что и 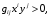
если
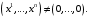 Такие квадратичные формы называются положительно определенными.
Такие квадратичные формы называются положительно определенными.Таким образом, формула (7.9) утверждает, что скалярное произведение двух векторов является билинейной, симметричной и положительно определенной формой от их координат.
Определение 7.9. Форма
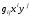 называется метрической формой данного базиса
называется метрической формой данного базиса 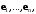 а ее коэффициенты
а ее коэффициенты 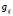 – коэффициентами этого базиса.
– коэффициентами этого базиса.Пример 7.9. Система координат
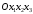 задается репером
задается репером 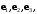 базис которого характеризуется метрическими коэффициентами, составляющими матрицу Грамма
базис которого характеризуется метрическими коэффициентами, составляющими матрицу Грамма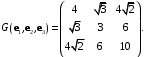
Найти длины базисных векторов и угол между ними.
Решение. Длины базисных векторов находятся из диагональных метрических коэффициентов:
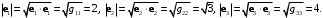
Далее
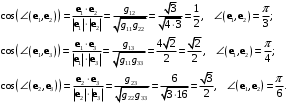
-
Формулы преобразования метрических коэффициентов при замене базиса.