ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.01.2024
Просмотров: 47
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пусть
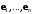 и
и 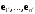 – два базиса,
– два базиса,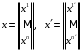
столбцы координат одного и того же базиса
 в этих базисах,
в этих базисах, 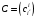 – матрица перехода от базиса
– матрица перехода от базиса 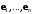 к базису
к базису 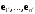 и
и 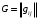 – матрица метрических коэффициентов базиса
– матрица метрических коэффициентов базиса 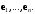 Тогда
Тогда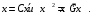
Кроме того,
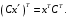 Поэтому
Поэтому 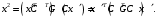
Эта формула означает, что матрица
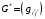 метрических коэффициентов базиса
метрических коэффициентов базиса 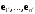 выражается формулой
выражается формулой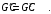 (7.16)
(7.16)Иначе говоря,
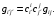 (7.17)
(7.17)Пример 7.10. Найти косинус угла
 между векторами
между векторами 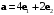 и
и 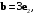 зная метрические коэффициенты
зная метрические коэффициенты 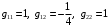 базиса
базиса 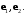
Решение. Для нахождения косинуса угла между заданными векторами воспользуемся формулой (7.5):
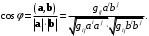
Нахождение числителя и знаменателя целесообразно провести в матричной форме считая, что матрица метрических коэффициентов имеет вид
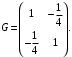
Тогда
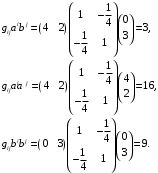
Таким образом, получим
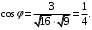
Пример 7.11. В базисе
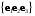 матрица метрических коэффициентов
матрица метрических коэффициентов 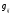
евклидового пространства
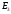 имеет вид
имеет вид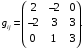
Формулы нового базиса выражаются через векторы базиса
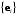 следующим образом:
следующим образом: 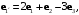
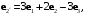
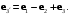 Найти:
Найти: 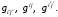
Решение. Матрица метрических коэффициентов выражается формулой (7.16). Для нахождения соответственной матрицы нужно найти матрицу перехода
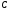 от базиса
от базиса 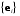 к базису
к базису 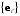 Имеем
Имеем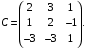
Тогда
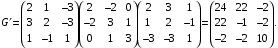
2) Матрица
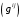 является обратной к матрице
является обратной к матрице 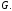 Поэтому
Поэтому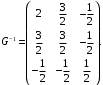
3) ) Матрица
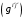 является обратной к матрице
является обратной к матрице 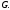 Поэтому
Поэтому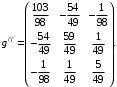
Вопросы для самоконтроля
-
Что называют скалярным произведением? -
Свойства скалярного произведения. -
Евклидово пространство. -
Длина вектора и угол между векторами. -
Неравенство Коши-Буняковского-Шварца. -
Сформулируйте теорему о неравенстве треугольника. -
Ортогональные векторы. Теорема Пифагора. -
Билинейные, симметричные и положительно определенные формы. -
Метрические формы и метрические коэффициенты. -
Формулы преобразования метрических коэффициентов при замене базиса.
Задания для самостоятельного решения
-
Вычислить скалярное произведение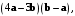 если известно, что
если известно, что  и
и 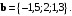
-
Вычислить косинус угла между векторами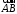 и
и 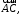 если известны координаты точек
если известны координаты точек 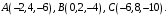
-
Вычислить ортогональную проекцию вектора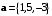 на направление вектора
на направление вектора 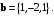
-
Вычислить модуль вектора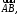 если
если 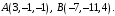
-
Найти проекцию вектора на направление вектора
на направление вектора  если
если 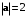 и
и 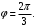
-
По заданному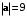 и
и 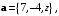 найти координату
найти координату 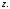
-
Даны вершины треугольника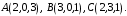 Определить внешний угол при вершине
Определить внешний угол при вершине 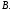
-
Найти скалярное произведение векторов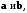 если известны их модули
если известны их модули 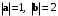 и угол
и угол 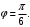
-
Установить связь между неравенством Коши–Буняковского и областью допустимых значений функции cos ϕ. -
Система координат задается репером
задается репером  базис которого характеризуется метрическими коэффициентами, составляющими матрицу Грамма
базис которого характеризуется метрическими коэффициентами, составляющими матрицу Грамма
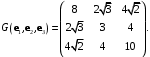
Найти длины базисных векторов и угол между ними.
Тест
1. Скалярное произведение векторов – это:
а) абсолютная величина этих векторов;
б) вектор;
+в) число;
г) сумма векторов.
2.Среди представленных формул стоит выбрать ту, что соответствует скалярному произведению:
+а)
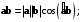
б)

в)
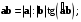
г)
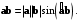
3.Чему равно скалярное произведение векторов, если угол между ними 900:
а) любому числу;
б) нулю;
в) положительному числу;
г) отрицательному числу.
4. Если скалярное произведение равно отрицательному числу, то этот угол межу векторами:
а) прямой;
б)развернутый;
+в) тупой;
г) острый.
5. Укажите соответствие:

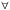


 .
.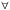
 и
и 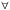



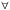


 Положительность.
Положительность. 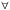
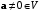

3а) Дистрибутивность;
1б) Коммутативность;
2в) Ассоциативность;
4г) Положительность.
6. Длина вектора определяется по формуле:
а)
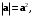
б)
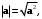
в)
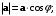
г)
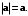
7. Укажите неравенство Коши - Буняковского – Шварца.
+а)
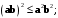
б)
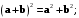
в)

г)

8. Если скалярное произведение равно нулю, то векторы называются:
а) сонаправленными;
б) равными;
+в) ортогональными;
г) коллинеарными.
9. Общая формула метрической формы имеет вид:
а)
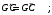
б)
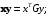
в)

+г)
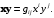
10.При n=2, метрическая форма имеет вид:
а)

б)
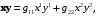
+в)
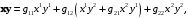
г)
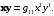
11. Метрические коэффициенты выражаются формулой:
+а)
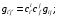
б)
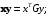
в)

г)
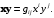
12. Линейное пространство
 для которого выбрано и зафиксировано некоторое скалярное произведение, называется
для которого выбрано и зафиксировано некоторое скалярное произведение, называется+а) евклидовым пространством;
б) векторным пространством;
в) аффинным пространством;
г) ассоциативным пространством.
13. При каком значении x векторы
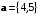 и
и 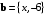 перпендикулярны.
перпендикулярны.а) 7,3;
б) 7;
+в) 7,5;
г) 8.
14. Косинус угла между двумя векторами равен 300. Чему будет равняться их скалярное произведение, если их длина равна 3 и 4?
а)
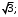
б)
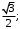
в)
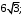
г)
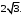
15. Найдите угол BAC треугольника ABC с координатами точек
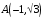 ,
, 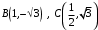 :
:. а) 45°;
б) 60°;
в) 50°;
+г) 90°.