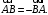ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.01.2024
Просмотров: 49
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема 2. Аффинные пространства
-
Аффинные пространства. -
Изоморфизм аффинных пространств одной и той же размерности. -
Аффинные координаты. -
Формулы преобразования аффинных координат точек.
-
Аффинное пространство
-
Аффинный репер
Определение 2.1. Репером в геометрическим пространстве называется набор
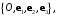состоящий из точки 
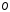и базиса 
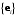векторного пространства 
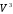свободных векторов геометрического пространства.Определение 2.2. Радиусом точки
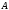относительно репера 
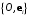называется вектор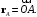 
Определение 2.3. Координатами точки
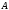относительно репера 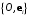называются координаты 
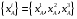ее радиуса 
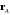относительно базиса 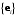векторного пространства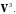 
Таким образом,
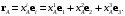(2.1)-
Аффинное пространство
Определение 2.4. Аффинным пространством называется тройка
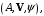состоящая из некоторого множества 
элементами которого являются точки, векторного пространства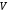 
и отображения 
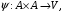относящего упорядоченной паре точек 
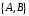множества 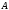некоторый вектор из 
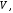обозначаемый
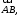такого, что выполняются следующие аксиомы:-
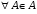и 
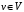
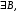что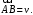 
-
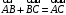
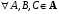(равенство треугольника).
Определение 2.5. Размерностью
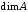аффинного пространства 
называется размерность ассоциированного векторного пространства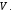
Из определения аффинного пространства выведем два соотношения:
Пример 2.1. Найдите координаты точек
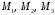относительно аффинного репера 
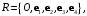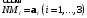если 
и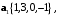 
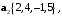
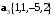в базисе 
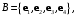и 
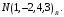
Решение. Координаты точек
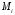в репере 
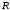совпадают с координатами их радиус-векторов 
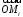в базисе 
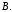В соответствии с аксиомами аффинного пространства 
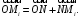Координаты вектора 
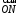в базисе 
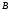совпадают с координатами точки 
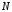в репере 
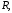координаты векторов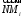 
известны. Следовательно, точка
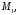например, имеет координаты 
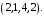Аналогично можно найти координаты остальных точек: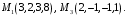 
-
Изоморфизм аффинных пространств одной и той же размерности.
Определение 2.6. Пусть
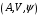и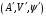 
– два аффинных пространства. Изоморфизмом пространства на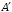 
называется такое биективное отображение 
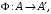если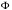 
индуцирует изоморфизм ассоциированных векторных пространств, то есть если существует изоморфизм 
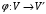такой, что
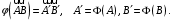(2.2)Если
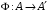– изоморфизм аффинных пространств, то изоморфизм векторных пространств 
определяемых соотношением (2.2), называется изоморфизмом, ассоциированным с изоморфизмом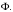 
Из условия (2.2) следует, что если
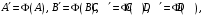
то
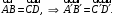(2.3)При выполнении условия (2.3) отображение
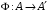индуцирует некоторое отображение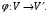 
Пространства
и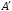 
называются изоморфными, если существует хотя бы один изоморфизм пространства на пространство 
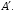То есть отношение изоморфности аффинных пространств является отношением эквивалентности.Теорема 2.1. Любые два аффинные пространства одной размерност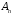и
и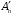 
изоморфны.
Доказательство. Пусть
– произвольный репер в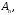 
а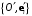 
– произвольный репер в 
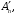тогда отображение 
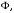относящее точке 
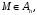имеющей координаты 
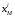относительно репера 
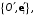является изоморфизмом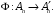 
-
Аффинные координаты.
Определение 2.7. Совокупность, состоящая из точки
и базиса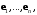 
называется координатной системой в 
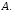Обозначается символом 
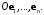Точка называется началом отсчета (координат).Пусть
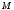– точка аффинного пространства 
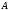и пусть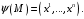 
Определение 2.8. Числа
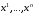называются аффинными координатами точки 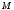в аффинной координатной системе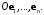 Эти координаты являются ничем иным, как координатами радиус-вектора
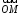в базисе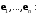 
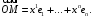(2.4)Пример 2.2. В некоторой аффинной системе координат известны координаты вершин треугольной пирамиды
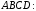
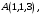
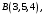
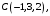
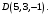Найти координаты (в той же системе координат):1) точки
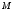пересечения медиан треугольника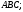 
2) точки
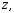которая делит отрезок 
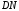в отношении 
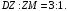.Решение. 1) Найдем координаты точки
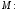
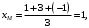
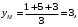
Следовательно, точка
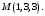
2) Найдем координаты точки
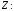
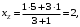
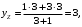
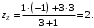
Следовательно, точка
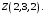
Пример 2.3. Векторы
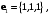
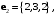
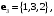
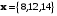заданы своими координатами в некотором базисе трёхмерного пространства. Векторы 
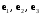также образуют базис пространства. Найти координаты вектора 
в этом базисе. Решение. Координаты вектора
в базисе 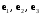– это коэффициенты разложения по базису (2.4). Имеем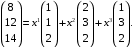
Учитывая, что векторы складывают и умножаются на число покоординатно, уравнение 2.4 примет вид системы линейных уравнений:
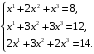
Решим систему методом Гаусса:
