ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.01.2024
Просмотров: 50
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Таким образом, получаем:
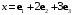 и вектор
и вектор  имеет координаты
имеет координаты 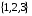 в базисе
в базисе 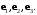
-
Формулы преобразования аффинных координат точек.
Рассмотрим на плоскости две аффинные системы координат:
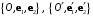 и пусть даны точки
и пусть даны точки 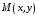 и
и 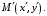
Преобразование координат состоит в следующем: выразить старые координаты
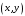 точки через новые
точки через новые 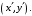
Зададим систему:
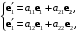
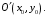 (2.5)
(2.5)По правилу треугольника получим:
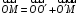
или
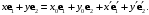
Используем (2.5):
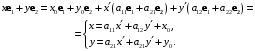 (2.6)
(2.6)Определение 2.9. Формулы (2.6) называются формулами преобразования координат.
Заметим, что матрица
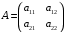 перехода от базиса
перехода от базиса  к базису
к базису 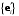 в точности совпадает с матрицей из коэффициентов при
в точности совпадает с матрицей из коэффициентов при 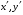 в формулах (2.6). Определитель этой матрицы
в формулах (2.6). Определитель этой матрицы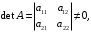
поэтому система (2.6) разрешима относительно
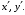
Интересны два частных случая:
-
Перенос начала.
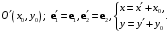
-
Замена координатных векторов.
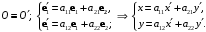
Пример2.4.Написать формулы преобразования координат в аффинной системе, если
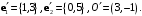
Решение. Имеем
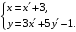
Пример 2. Показать, что формулы
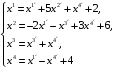
можно рассматривать как формулы преобразования координат точек аффинного пространства
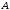 при переходе от одного репера к другому. Указать новые координаты точки
при переходе от одного репера к другому. Указать новые координаты точки 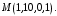 Найти точку
Найти точку 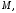 соответствующие координаты которой в новом и старом реперах совпадают.
соответствующие координаты которой в новом и старом реперах совпадают.Решение. Найдем определитель матрицы, составленной из коэффициентов при
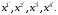 Раскрывая определитель по первому столбцу, находим:
Раскрывая определитель по первому столбцу, находим: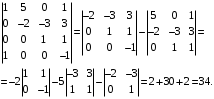
Так как найденный определитель отличен от нуля, данные в условии формулы можно рассматривать как формулы преобразования координат точек аффинного пространства
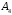 при переходе от одного репера к другому.
при переходе от одного репера к другому.Для того чтобы найти новые координаты точки
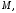 подставим ее старые координаты в исходные формулы:
подставим ее старые координаты в исходные формулы: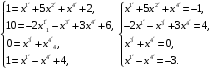
Решая полученную систему, находим
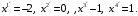
Следовательно,
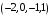 – новые координаты точки
– новые координаты точки 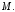
Если старые и новые координаты точки совпадают, то они являются решениями следующей системы уравнений:
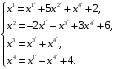
Перенесем слагаемые в каждом равенстве в одну часть, получим:
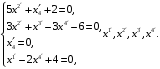
откуда находим
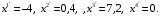
Таким образом,
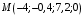 – искомая точка.
– искомая точка.Вопросы для самоконтроля
-
Дайте определение аффинного репера. -
Аффинные пространства. -
Как определить размерность аффинного пространства? -
Изоморфизм аффинных пространств одной и той же размерности. -
Аффинные координаты. -
Формулы преобразования аффинных координат точек.
Задачи для самостоятельного решения
-
Даны вершины треугольника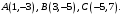 Определить середины его сторон.
Определить середины его сторон. -
Даны две точки: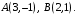 Найти координаты точки
Найти координаты точки 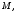 симметричные точке А относительно точки В и координаты точки
симметричные точке А относительно точки В и координаты точки 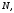 симметричные точки В относительно точки А.
симметричные точки В относительно точки А. -
Найдите координаты точек относительно аффинного репера
относительно аффинного репера 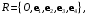 если
если 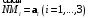 и
и 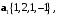
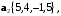
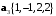 в базисе
в базисе 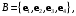 и
и 
-
Написать формулы преобразования координат, если начало координат перенесено в точку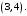
-
Отрезок с концами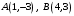 разделен на три равные части. Найти координаты точек деления.
разделен на три равные части. Найти координаты точек деления. -
Векторы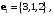
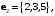
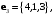
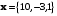 заданы своими координатами в некотором базисе трёхмерного пространства. Векторы
заданы своими координатами в некотором базисе трёхмерного пространства. Векторы  также образуют базис пространства. Найти координаты вектора
также образуют базис пространства. Найти координаты вектора  в этом базисе.
в этом базисе. -
Векторы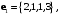
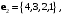
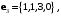
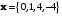 заданы своими координатами в некотором базисе трёхмерного пространства. Векторы
заданы своими координатами в некотором базисе трёхмерного пространства. Векторы  также образуют базис пространства. Найти координаты вектора
также образуют базис пространства. Найти координаты вектора  в этом базисе.
в этом базисе. -
Даны две аффинные системы координат: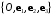 (старая система координат) и
(старая система координат) и 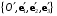 (новая система координат). Матрица перехода от базиса
(новая система координат). Матрица перехода от базиса 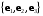 к базису
к базису 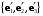 имеет вид:
имеет вид:
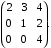
Координаты точки
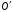 относительно старой аффинной системы координат равны
относительно старой аффинной системы координат равны 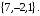 Найти формулы преобразования координат.
Найти формулы преобразования координат.-
Выведите формулы замены базиса и замены системы координат на прямой линии. Как меняются координаты точек прямой, если при неизменном начале координат длина базисного вектора увеличивается вдвое? -
Определить аффинное преобразование, которое три данные точки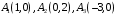 переводит в точки
переводит в точки 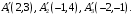
Тест
1. Тройка
 состоящая из некоторого множества
состоящая из некоторого множества  элементами которого являются точки, векторного пространства
элементами которого являются точки, векторного пространства  и отображения
и отображения  относящего упорядоченной паре точек
относящего упорядоченной паре точек  множества
множества  некоторый вектор из
некоторый вектор из  обозначаемый
обозначаемый  называется:
называется:а) линейным пространством;
б) векторным пространством;
в) евклидовым пространством;
+г) аффинным пространством.
-
Аффинные координаты точки в аффинной координатной системе
в аффинной координатной системе 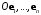 имеют вид:
имеют вид:
+а)
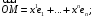
б)
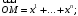
в)
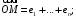
г)
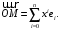
3. Укажите формулы преобразования координат:
а)
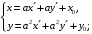
+б)
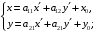
в)
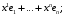
г)
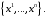
4. Совокупность, состоящая из точки

и базиса
 называется
называетсяа) изоморфизмом;
б) аффинным пространством;
в)координатной системой;
г) координатами точки в базисе.
5. Любые два аффинные пространства одной размерности
+а) изоморфны;
б)коллинеарны;
в)пересекаются;
г)коммутитивны.
6. Координаты точки
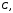 делящий отрезок
делящий отрезок 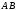 в отношении
в отношении 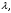 находятся по формулам:
находятся по формулам:+а)
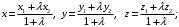
б)
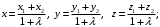
в)
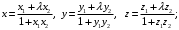
г)