Файл: Многочлены.doc

Факультет: высшего образования

Направление:

 

КУРСОВАЯ РАБОТА

по дисциплине: «Программирование»

на тему: «Многочлены»

студент группы шифр

ФИО

«____» ______________ 201 г.

_________________________

подпись студента)

 

Проверил

ФИО

Оценка _____________________

____________________________

(подпись преподавателя)

«___» ____________ 201 г.

 

Лысьва, 2013г.

Содержание

1. Введение

Изучение полиномиальных уравнений и их решений составляло едва ли не главный объект «классической алгебры». С изучением многочленов связан целый ряд преобразований в математике: введение в рассмотрение нуля, отрицательных, а затем и комплексных чисел, а также появление теории групп как раздела математики и выделение классов специальных функций в анализе.

Многочлены также играют ключевую роль в алгебраической геометрии, объектом которой являются множества, определённые как решения систем многочленов.

Поэтому создание легкой и доступной программы способной быстро выполнять нужные действия с многочленами любой степени является практичной и упрощает работу, избавляя нас от рутинных вычислений.

1.1 Цель работы

Научиться работать с классами и создать класс, в котором будет создан набор функций

---

, подпрограмм и тп для работы с многочленами от одной переменной (первый многочлен степени m, второй — степени n), а именно выполнять операции: сложения, умножения, вычитания, деления с остатком, возведения степень, операции отношения (равно, не равно), возведение в натуральную степень, вычисление производной от многочлена, вычисление значения в точке x₀.

1.2 Постановка задачи

Реализовать в виде класса набор подпрограмм для выполнения операций с многочленами от одной переменной (первый многочлен степени m, второй — степени n):

1) сложение;
2) вычитание;
3) умножение;
4) деление с остатком;
5) операции отношения (равно, не равно);
6) возведение в натуральную степень k;
7) вычисление производной от многочлена;
8) вычисление значения в точке x₀.
Многочлен представить массивом коэффициентов.

Используя этот класс, решить задачи:
1. Найти наибольший общий делитель многочленов P(x) и Q(x).
2. Вычислить: P^s(x) – Q^r(x).

1.3 Основная теория

Многочлен от n переменных — это сумма одночленов или, строго, — конечная формальная сумма вида.¹

, где

• 
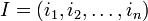   — набор из целых неотрицательных чисел, именуемый мультииндексом,
  
• 
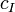   — число, именуемое коэффициент многочлена, зависящее только от мультииндекса I.
  

В частности, многочлен от одной переменной есть конечная формальная сумма вида

, где

• 
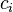   — фиксированные коэффициенты,
  
• 
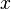   — переменная.
  

Привести многочлен к стандартному виду — означает привести к стандартному виду все его члены, а затем привести подобные члены.

---

¹

Сложить два многочлена — это значит представить их сумму  
в стандартном виде.  ¹

Чтобы решить многочлен, надо свести подобные члены. Например:
p1(x)=6x⁴-x⁵+5x⁴+x³; p2(x)=-8x⁴-4x³+5x+6;
p1+ p1=(6x⁴-x⁵+5x⁴+x³)+( -8x⁴-4x³+5x+6)= 6x⁴-x⁵+5x⁴+x³ -8x⁴-4x³+5x+6=6x⁴-x⁵-3x⁴-3x³+5x+6.

Вычесть из одного многочлена другой — это значит представить их разность в стандартном виде.¹

При вычитании многочленов важно помнить, что после раскрытия скобок знаки во втором многочлене меняются на противоположные.

Например:
p1(x) = 6x⁴ - x⁵ + 5x⁴ + x³; p2 (x)=- 8x⁴ - 4x³ + 5x+ 6;
p1- p1 =(6x⁴ – x⁵+ 5x⁴ + x³) - (-8x⁴ - 4x³ + 5x+ 6) = 6x⁴ - x⁵ + 5x⁴ + x³ + 8x⁴ + 4x³ - 5x- 6=6x⁴-x⁵+13x⁴+5x³-5x-6.

Умножить многочлен на многочлен - это значит, каждый член одного многочлена умножить на каждый член другого многочлена и полученные одночлены сложить. ¹

Например:
p1(x) = x²+6x-1; p2(x) = 3x+1;
p1*p1 =(x²+6x-1)*(3x+1)= 3x³+x² +6x²+6x-3x-1=3x³+7x²+3x³-1.

Деление многочленов — алгоритм деления многочлена   на многочлен  , степень

---

 которого меньше или равна степени многочлена  . Алгоритм представляет собой обобщенную форму деления чисел столбиком, легко реализуемую вручную.²

Пример:

1. Делим первый элемент делимого на старший элемент делителя, помещаем результат под чертой  .



2. Умножаем делитель на полученный выше результат деления (на первый элемент частного). Записываем результат под первыми двумя элементами делимого  .



3. Вычитаем полученный после умножения многочлен из делимого, записываем результат под чертой  .



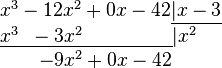
4. Повторяем предыдущие 3 шага, используя в качестве делимого многочлен, записанный под чертой.



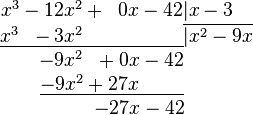
5. Повторяем шаг 4.



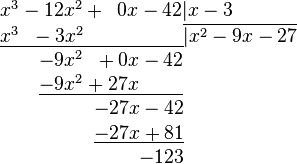
6. Конец алгоритма.

Таким образом, многочлен   — частное деления, а   — остаток.

Возведение многочлена в степень

Чтобы возвести двучлен в четвертую, пятую и т.д. степень, надо последовательно умножить разложенный многочлен на самого себя несколько раз.

Например:

p1(x)= (3x² – 2)³=(3x² – 2) (3x² – 2) (3x² – 2)= (3x² – 2)(9x² – 12x+4)= 27x³+54x

---

²+36x+8.

Два многочлена p1(x) и p2(x) считаются равными, если равны их коэффициенты при одинаковых степенях переменной х и свободные члены (равны их соответствующие коэффициенты). В этом случае пишут:p1 (x) =p2 (x).³

Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке).²

Для вычисления производной от многочлена нам потребуются знания таблицы производных:
(xⁿ)’=nx^n-1; c’=0.

Например:
p1(x)= 3x² – 2=6x.

Класс — разновидность абстрактного типа данных в объектно-ориентированном программировании, характеризуемый способом своего построения. Наряду с понятием «объекта» класс является ключевым понятием в ООП. Суть отличия классов от других абстрактных типов данных состоит в том, что при задании типа данных класс определяет одновременно и интерфейс, и реализацию для всех своих экземпляров, а вызов метода-конструктора обязателен. ³

На практике объектно-ориентированное программирование сводится к созданию некоторого количества классов, включая интерфейс и реализацию, и последующему их использованию. Графическое представление некоторого количества классов и связей между ними называется диаграммой классов.

Идея классов пришла из работ по базам знаний, имеющих отношение к исследованиям по искусственному интеллекту. Используемые человеком классификации в зоологии, ботанике, химии, деталях машин, несут в себе основную идею, что любую вещь всегда можно представить частным случаем некоторого более общего понятия. Конкретное яблоко — это в целом некоторое яблоко, вообще яблоко, а любое вообще яблоко — фрукт. Именно поэтому примеры классов в учебных пособиях по объектно-ориентированному программированию так часто упоминают яблоки и груши.

---