Файл: Расшифровка подписи Члены комиссии подпись расшифровка подписи.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 173
Скачиваний: 1
СОДЕРЖАНИЕ
1 Выбор электродвигателя и расчет основных параметров привода
1.2 Частота вращения вала двигателя
1.3 Требуемая частота вращения барабана
1.4 Общее передаточное число привода
1.5 Передаточное число ременной передачи
1.6 Частоты вращения валов (индекс соответствует номеру вала на схеме привода)
2.2 Определение допускаемых напряжений
2.4 Проверочный расчет передачи
3 Расчет и проектирование валов
3.3 Расчет тихоходного вала в сечении В
3.4 Расчет тихоходного вала в сечении С
3.5 Расчет тихоходного вала на статическую прочность
4.1 Расчет подшипников быстроходного вала на долговечность
4.2 Расчет подшипников тихоходного вала на долговечность
5.1 Расчет шпонок тихоходного вала
5.2 Расчет шпонок быстроходного вала
6 Расчет элементов корпуса редуктора
7Расчет клиноременной передачи
8.1 Смазка зубчатых колес, выбор сорта масла, контроль уровня масла
10 Схема подключения асинхронного нереверсивного электродвигателя
2 Расчет зубчатой передачи
2.1 Выбор материала
Для выбора материала необходимо определить наружный диаметр заготовки Dm и характерный размер заготовки для насадного зубчатого колеса Sm. Для этого воспользуемся формулами:
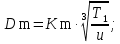
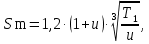
Где Т1 – крутящий момент на шестерне Н·м, Sm – характерный размер заготовки для насадного зубчатого колеса, u– передаточное число зубчатой передачи, km – коэффициент, учитывающий вид передачи (для косозубой цилиндрической передачи km = 20).
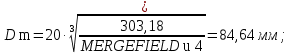
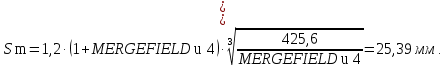
Диаметр заготовки колеса:
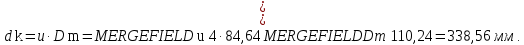
Выбираем материалы для зубчатых колес. Принимаем для колеса и шестерни сталь 45, термообработка для шестерни – улучшение, термообработка для колеса – нормализация; твердость поверхности зуба шестерни 235…262 НВ, твердость поверхности зуба колеса 179…207 НВ.
Средние значения твердости поверхности зуба шестерни и колеса:
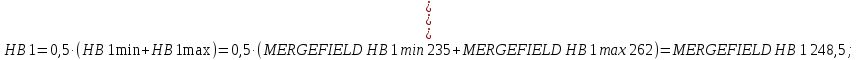
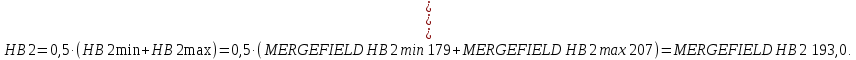
2.2 Определение допускаемых напряжений
2.2.1 Допускаемые контактные напряжения
Для их определения используем зависимость:
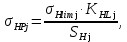
где j=1 для шестерни, j=2 для колеса, σHlim– предел контактной выносливости, KHL – коэффициент долговечности, SH– коэффициент безопасности.
Пределы контактной выносливости:
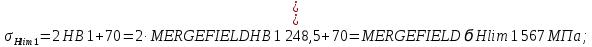
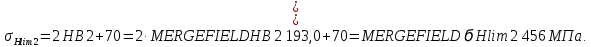
Коэффициенты безопасности для термообработки улучшение:
SH1 =1,1;SH2=1,1.
Коэффициенты долговечности:
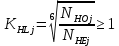
Базовые числа циклов при действии контактных напряжений:
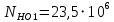 ;
;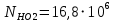 .
.Эквивалентные числа циклов напряжений:
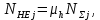
где μh=0,18 – коэффициент эквивалентности для средне нормального режима работы.
Суммарное число циклов нагружения:
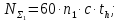
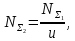
где с=1– число зацеплений за 1 оборот колеса, th – суммарное время работы передачи:
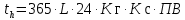
гдеL– срок службы передачи в годах, Кг – коэффициент использования в течение года, Кс – коэффициент использования в течение суток, ПВ – относительная продолжительность включения.
Здесь
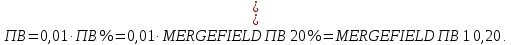
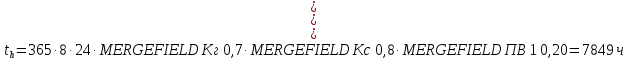
Суммарное число циклов нагружения:
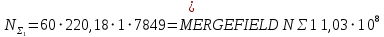 ;
;
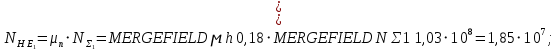
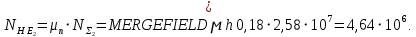
Поскольку
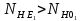 , примем
, примем 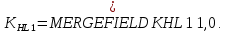
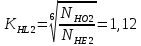
Определим допускаемые контактные напряжения для шестерни и колеса:
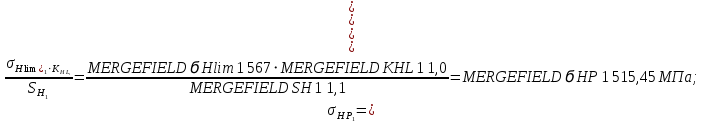
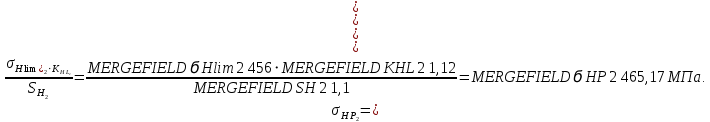
Допускаемые контактные напряжения для косозубой передачи:
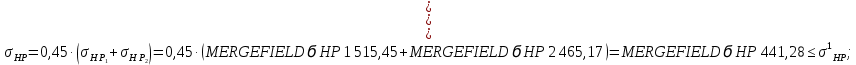
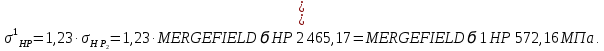
Условие
 выполняется.
выполняется.2.2.2 Допускаемые напряжения изгиба
Вычисляем по формуле:
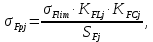
гдеσFlim – предел изгибной выносливости зубьев
, SF – коэффициент безопасности, KFC – коэффициент, учитывающий влияние двухстороннего приложения нагрузки, KFL – коэффициент долговечности.
Пределы изгибной выносливости зубьев:
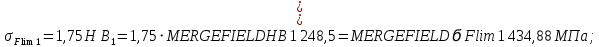
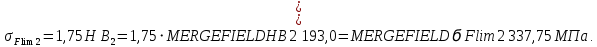
Коэффициенты безопасности при изгибе:
SF1=1,7; SF2=1,7.
Коэффициенты, учитывающие влияние двухстороннего приложения нагрузки, для нереверсивного привода:
KFC1=1,00; KFC2=1,00.
Коэффициенты долговечности:
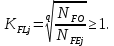
гдеqj – показатель степени кривой усталости, q1=6, q2=6,
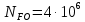 – базовое число циклов при изгибе.
– базовое число циклов при изгибе.Эквивалентное число циклов напряжений при изгибе:
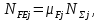
где μF1=0,14 и μF2=0,14– коэффициенты эквивалентности для средне нормального режима работы.Тогда:
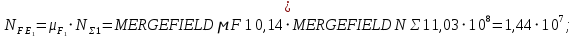
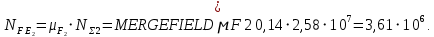
Поскольку
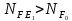 , примем
, примем 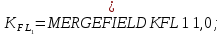
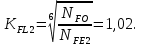
Определим допускаемые напряжения изгиба для шестерни и колеса:

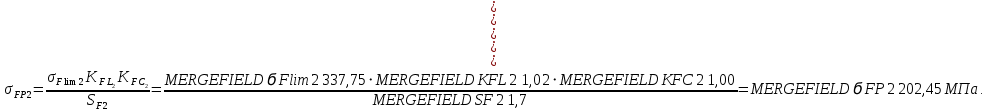
2.3 Проектный расчет передачи
2.3.1 Межосевое расстояние
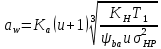
Где Ка=410 для косозубых передач.
Примем коэффициент ширины зубчатого венца для косозубой передачи ψba=0,400. На этапе проектного расчета задаемся значением коэффициента контактной нагрузки KH=1,2. Тогда:

Полученное межосевое расстояние округлим до ближайшего большего стандартного значения aw=224 мм.
2.3.2 Модуль, числа зубьев колес и коэффициенты смещения
Рекомендуемый диапазон для выбора модуля:

Из полученного диапазона выбираем стандартный модуль mn =
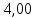 мм.
мм.Суммарное число зубьев передачи:
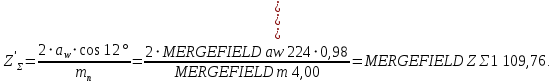
Полученное значение
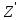 округлим до ближайшего целого числа Z∑ = 110 и определим делительный угол наклона зуба:
округлим до ближайшего целого числа Z∑ = 110 и определим делительный угол наклона зуба: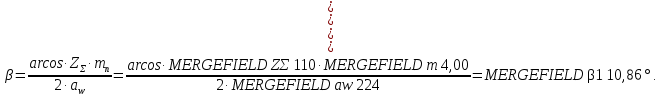
Число зубьев шестерни:
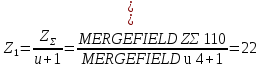
Число зубьев колеса:
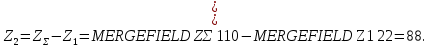
Фактическое передаточное число:
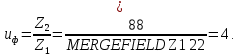
При u<4,5 отличие фактического передаточного числа от номинального должно быть не больше 2,5%.
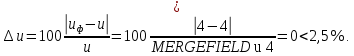
Учитывая, что Z1>17, принимаем коэффициент смещения x1=0, x2=0
2.3.3 Ширина зубчатых венцов и диаметры колес
Ширина зубчатого венца колеса:
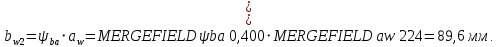
Округлим bw2 до ближайшего числа из ряда нормальных линейных размеров bw2=90 мм. Ширину зубчатого венца шестерни bw1 примем bw1=95 мм.
Определим диаметры окружностей зубчатых колес:
-делительные окружности:
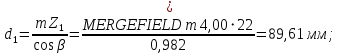
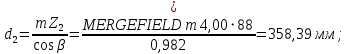
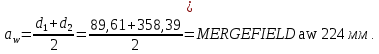
-окружности вершин зубьев
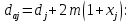
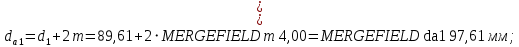
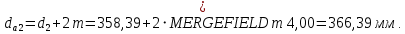
-окружности впадин зубьев
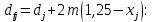
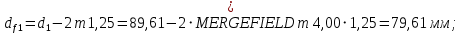
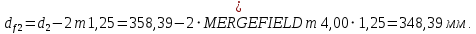
2.3.4 Окружная скорость в зацеплении и степень точности передачи
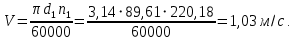
Для полученной скорости назначим степень точности передачи nст=8, учитывая, что nст=9 для закрытых зубчатых передач применять не рекомендуется.
2.4 Проверочный расчет передачи
2.4.1 Проверка контактной прочности зубьев
Используем формулу:
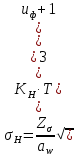
где Zσ=8400 для косозубых передач.
Коэффициент контактной нагрузки:
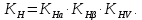
Коэффициент неравномерности распределения нагрузки между зубьями:
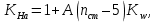
где А=0,15 для косозубых передач,Kw – коэффициент, учитывающий приработку зубьев.
При НВ2
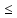 350 используем формулу:
350 используем формулу: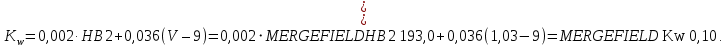
Тогда:
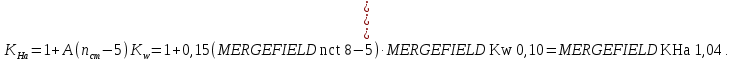
Коэффициент неравномерности распределения нагрузки по ширине колеса:
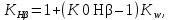
где K0Hβ – коэффициент неравномерности распределения нагрузки в начальный период работы.