Файл: Расшифровка подписи Члены комиссии подпись расшифровка подписи.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 179
Скачиваний: 1
СОДЕРЖАНИЕ
1 Выбор электродвигателя и расчет основных параметров привода
1.2 Частота вращения вала двигателя
1.3 Требуемая частота вращения барабана
1.4 Общее передаточное число привода
1.5 Передаточное число цепной передачи
1.6 Частоты вращения валов (индекс соответствует номеру вала на схеме привода)
2.2 Определение допускаемых напряжений
2.4 Проверочный расчет передачи
3 Расчет и проектирование валов
3.3 Расчет тихоходного вала в сечении В
3.4 Расчет тихоходного вала в сечении С
3.5 Расчет тихоходного вала на статическую прочность
4.1 Расчет подшипников быстроходного вала на долговечность
4.2 Расчет подшипников тихоходного вала на долговечность
5.1 Расчет шпонок тихоходного вала
5.2 Расчет шпонок быстроходного вала
6 Расчет элементов корпуса редуктора
8.1 Смазка зубчатых колес, выбор сорта масла, контроль уровня масла
9 Схема подключения асинхронного нереверсивного электродвигателя
Для определения K0Hβ найдем коэффициент ширины венца по диаметру:
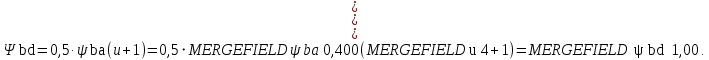
По значению Ψbdопределим K0Hβ=

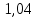 .Тогда:
.Тогда: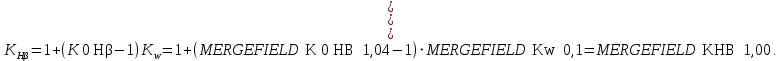
Динамический коэффициент KHV=

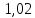 определим методом линейной интерполяции.
определим методом линейной интерполяции.Окончательно найдем:
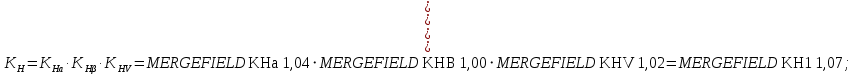
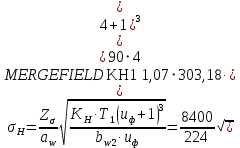
2.4.2 Проверка изгибной прочности зубьев
Напряжения изгиба в зубе шестерни:
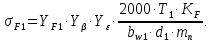
Коэффициент формы зуба при xj=0:
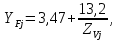
где
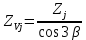 – эквивалентное число зубьев.
– эквивалентное число зубьев.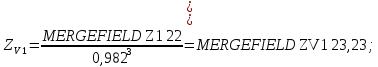
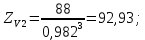

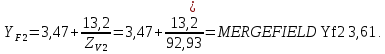
Коэффициент, учитывающие влияние угла наклона зуба на его прочность:
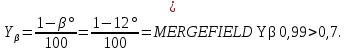
Коэффициент торцевого перекрытия:
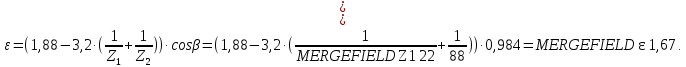
Коэффициент, учитывающие перекрытие зубьев:
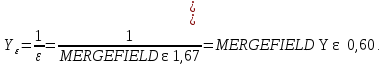
Коэффициент нагрузки при изгибе:
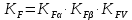
Для определения его коэффициентов используем зависимости:

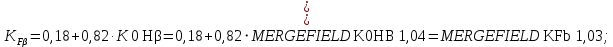
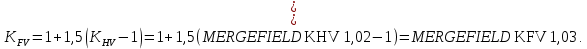
Тогда:
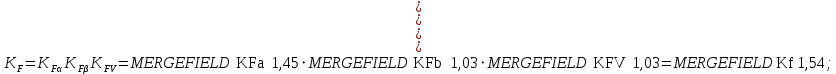
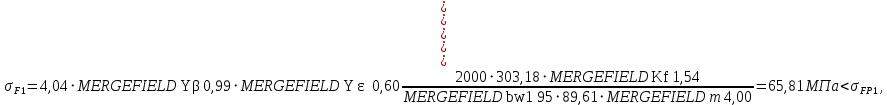
где
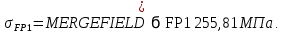
Напряжение в зубьях колеса:
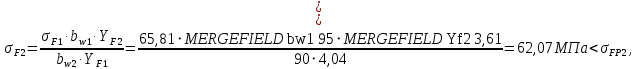
где
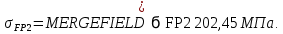
2.5 Силы в зацеплении
Окружная сила:
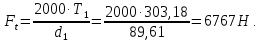
Распорная сила:
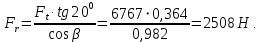
Осевая сила:
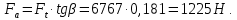
Суммарная сила:
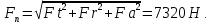
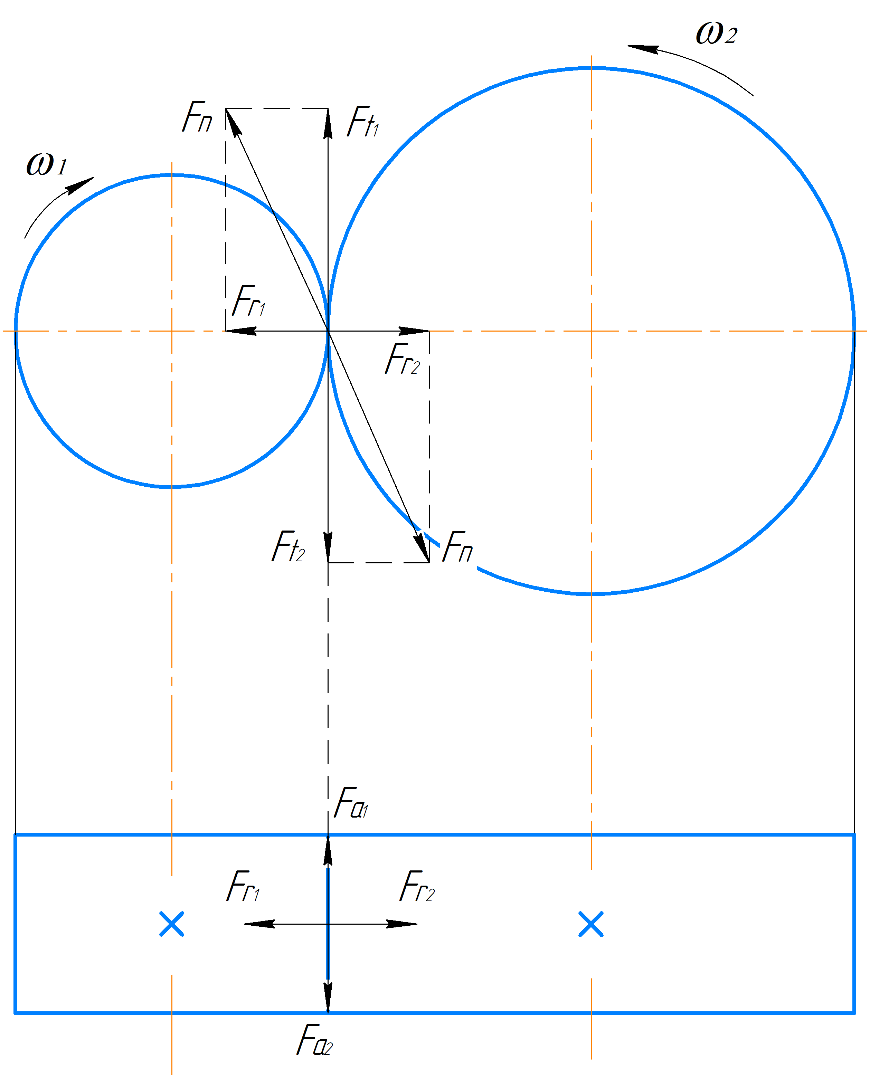
Рисунок 1 – Схема расположения зубчатых сил в зацеплении
3 Расчет и проектирование валов
3.1 Расчет быстроходного вала
3.1.1 Предварительный расчет быстроходного вала
Расчет выполняется на кручение по пониженным допускаемым напряжениям [????????] МПа. Ориентировочно определим диаметр вала в наименьшем сечении:
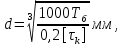
где
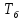 Нм – крутящий момент в опасном сечении вала, [????????]МПа – пониженные допускаемые напряжения на кручение, σbМПа – предел прочности материала вала.
Нм – крутящий момент в опасном сечении вала, [????????]МПа – пониженные допускаемые напряжения на кручение, σbМПа – предел прочности материала вала.Твердость заготовки 235…262 HB; σb=780МПа.
Тогда допускаемое напряжение на кручение:
[????????]= 0,025
 σb = 0,025
σb = 0,025  780 = 19,5 МПа.
780 = 19,5 МПа.Тогда диаметр хвостовика вала
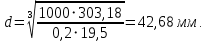
Принимаем диаметр d = 45 мм из нормального ряда линейных размеров.
Консольная нагрузка:
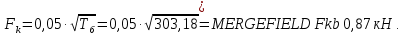
3.1.2 Определение опорных реакций
Горизонтальная плоскость
Σm(F)B= 0
Fa· 0,5d1 – Fr· L3 + RDг· L0 = 0
RDг =
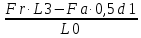 =
= 
= 0,984 кН.
Σm(F)D= 0
Fr · L3 +Fa ·0,5d1 – RBг· L0 = 0
RBг =
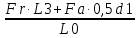 =
= 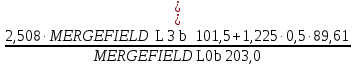 =1,524 кН.
=1,524 кН.Проверка:
ΣFу= 0
RВг–Fr + RDг = 0
1,524 –2,508 + 0,984 = 0
Вертикальная плоскость
Σm(F)D= 0
Ft· L3 – RBв· L0 + Fk· (Lk+ L0) = 0
RBв =
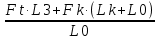 =
= 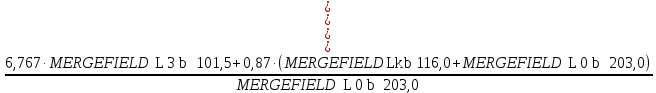 =4,751 кН.
=4,751 кН.Σm(F)B =0
Fk· Lk –Ft· L3 + RDв· L0 = 0
RDв =
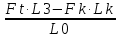 =
= 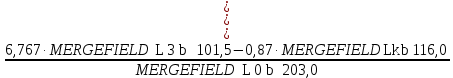 =2,886 кН.
=2,886 кН.Проверка:
ΣFу= 0
–Fk + RВв–Ft + RDв = 0
–0,87+ 4,751 –6,767+ 2,886= 0
3.1.3 Построение эпюр изгибающих и крутящих моментов для быстроходного вала
Изгибающие моменты в сечении С (горизонтальная плоскость)
МхСВ = L3· RBг = 101,5 · 1,524= 154,69 Нм;
МхСD = МхСВ – 0,5d1 Fa = 154,69 – 0,5·89,61·1,225= 99,8 Нм.
Изгибающие момент в сечении B (вертикальная плоскость)
МуВ = –Lk·Fk = –116,0· 0,87=-100,92 Нм.
Изгибающие момент в сечении С (вертикальная плоскость)
МуС = –(Lk + L3)·Fk +L3·RBв = – (116 + 101,5)·0,87 +101,5·4,751= 293 Нм.
Суммарный изгибающий момент
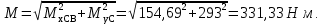
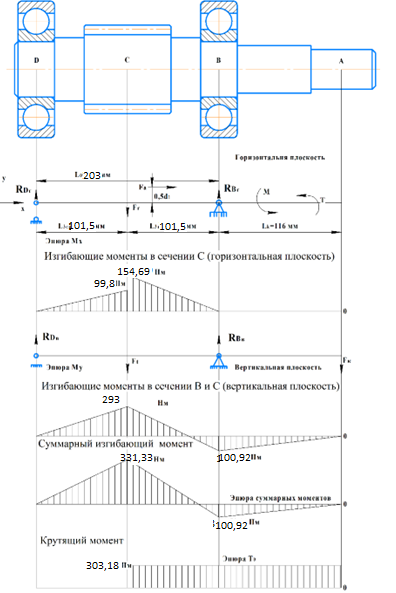
Рисунок 2 – Эпюры изгибающих и крутящих моментов на быстроходном валу
3.2 Расчет тихоходного вала
3.2.1 Предварительный расчет тихоходного вала
Расчет выполняется на кручение по пониженным допускаемым напряжениям [????????] МПа. Ориентировочно определим диаметр вала в наименьшем сечении:
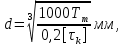
где
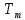 Нм – крутящий момент в опасном сечении вала, [????????]МПа – пониженные допускаемые напряжения на кручение, σb МПа – предел прочности материала вала.
Нм – крутящий момент в опасном сечении вала, [????????]МПа – пониженные допускаемые напряжения на кручение, σb МПа – предел прочности материала вала.Твердость заготовки 179…207 HB; σb=600МПа.
Тогда допускаемое напряжение на кручение
[????????]= 0,025
 σb = 0,025
σb = 0,025  600 = 15 МПа.
600 = 15 МПа.Тогда диаметр хвостовика вала
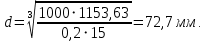
Принимаем диаметр d = 75 мм из нормального ряда линейных размеров.
Консольная нагрузка:
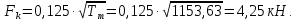
3.2.2 Определение опорных реакций
Горизонтальная плоскость
Σm(F)B= 0
Fa· 0,5d1 – Fr· L3 + RDг· L0 = 0
RDг =
 =
= 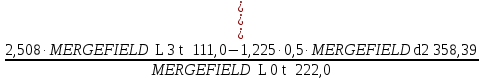 = 0,265 кН.
= 0,265 кН.Σm(F)D= 0
Fr · L3 +Fa ·0,5d1 – RBг· L0 = 0
RBг =
 =
= 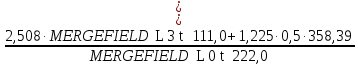 =2,243 кН.
=2,243 кН.Проверка:
ΣFу= 0
RВг– Fr + RDг = 0
2,243– 2,508 +0,265 = 0
Вертикальная плоскость
Σm(F)D= 0
Ft· L3 – RBв· L0 +Fk· (Lk+ L0) = 0
RBв =
 =
= 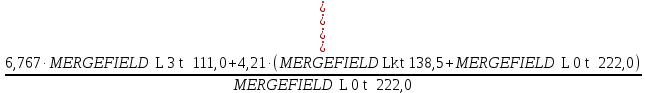 = 10,22 кН.
= 10,22 кН.Σm(F)B =0
Fk· Lk –Ft· L3 + RDв· L0 = 0
RDв =
