Файл: Расшифровка подписи Члены комиссии подпись расшифровка подписи.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 183
Скачиваний: 1
СОДЕРЖАНИЕ
1 Выбор электродвигателя и расчет основных параметров привода
1.2 Частота вращения вала двигателя
1.3 Требуемая частота вращения барабана
1.4 Общее передаточное число привода
1.5 Передаточное число цепной передачи
1.6 Частоты вращения валов (индекс соответствует номеру вала на схеме привода)
2.2 Определение допускаемых напряжений
2.4 Проверочный расчет передачи
3 Расчет и проектирование валов
3.3 Расчет тихоходного вала в сечении В
3.4 Расчет тихоходного вала в сечении С
3.5 Расчет тихоходного вала на статическую прочность
4.1 Расчет подшипников быстроходного вала на долговечность
4.2 Расчет подшипников тихоходного вала на долговечность
5.1 Расчет шпонок тихоходного вала
5.2 Расчет шпонок быстроходного вала
6 Расчет элементов корпуса редуктора
8.1 Смазка зубчатых колес, выбор сорта масла, контроль уровня масла
9 Схема подключения асинхронного нереверсивного электродвигателя
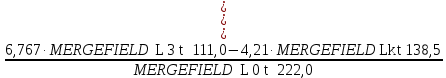 =0,76 кН.
=0,76 кН.Проверка:
ΣFу= 0
–Fk + RВв–Ft + RDв = 0
–4,21+ 10,22–6,767 +0,76= 0
3.2.3 Построение эпюр изгибающих и крутящих моментов для тихоходного вала
Изгибающие моменты в сечении С (горизонтальная плоскость)
МхСВ = L3· RBг = 111,0 · 2,243= 249 Нм;
МхСD = МхСВ – 0,5d2 Fa = 249– 0,5·358,39· 1,225= 29,5 Нм.
Изгибающие момент в сечении B (вертикальная плоскость)
МуВ = –Lk·Fk = –138,5· 4,21=-583 Нм.
Изгибающие момент в сечении С (вертикальная плоскость)
МуС = –(Lk + L3)·Fk +L3·RBв = –(138,5 + 111)·4,21+111·10,22= 84 Нм.
Суммарный изгибающий момент
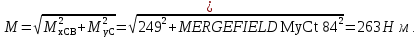
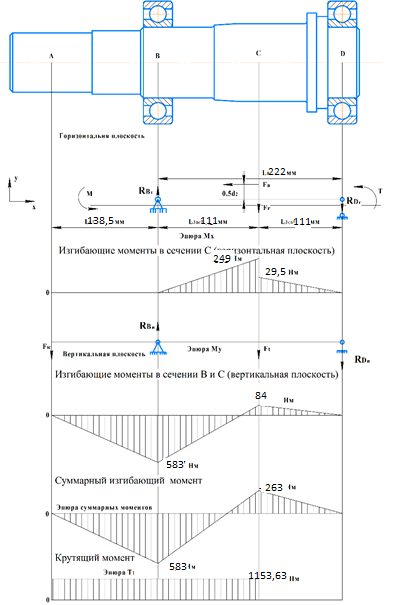
Рисунок 3 – Эпюры изгибающих и крутящих моментов на тихоходном валу
3.3 Расчет тихоходного вала в сечении В
1) Определение нагрузок
В сечении действуют:
Изгибающий момент M= 583 Нм;
Крутящий момент Тт = 1153,63 Нм;
Осевая сила Fa= 1,225 кН.
2) Геометрические характеристики опасного сечения
Значения площади поперечного сечения A, осевого
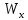 и полярного
и полярного 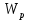 моментов сопротивлений для типовых поперечных сечений определяют по формулам.
моментов сопротивлений для типовых поперечных сечений определяют по формулам.Осевой момент сопротивления:
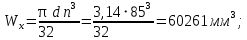
Полярный момент сопротивления:
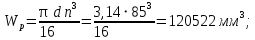
Площадь сечения:
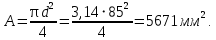
3) Определение напряжений
Напряжения изгиба меняются по симметричному циклу с амплитудой:
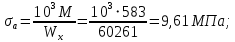
Средние нормальные напряжения:
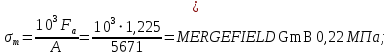
Касательные напряжения меняются по отнулевому циклу:
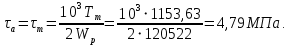
4) Пределы выносливости
Пределы выносливости материала при симметричном цикле изгиба и кручения определяются по следующим формулам:
для углеродистых сталей:
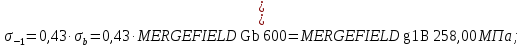
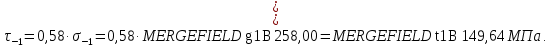
здесь
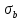 – предел прочности материала вала
– предел прочности материала вала5) Эффективные коэффициенты концентрации напряжений и коэффициенты влияния размера поперечного сечения.
Для посадки с натягом
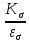 определяется из Табл. 7,5
определяется из Табл. 7,5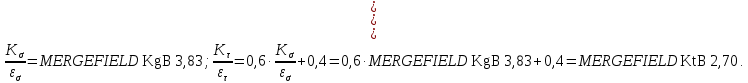
6) Коэффициент влияния шероховатости поверхности.
Поверхность вала под подшипник получена чистовым шлифованием с
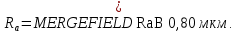
KF – коэффициент влияния шероховатости поверхности, определяется в зависимости от
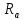 KF=
KF=
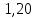 .
.7)Коэффициент чувствительности к асимметрии цикла.
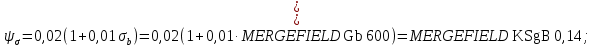
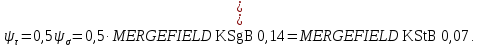
8) Коэффициент влияния упрочнения.
Примем, что на участке вала с опасным сечением упрочнение отсутствует.
KV - коэффициент влияния упрочнения, KV=1.
9) Коэффициенты перехода от пределов выносливости образца к пределам выносливости детали.
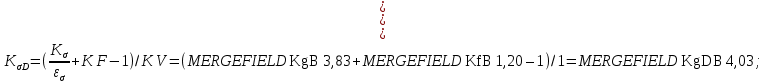
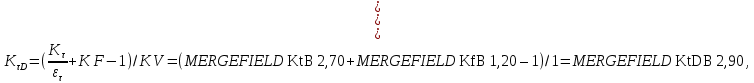
где
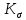 и
и 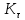 - эффективные коэффициенты концентрации напряжений
- эффективные коэффициенты концентрации напряжений 10) Коэффициенты запаса прочности
Значения
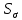 и
и 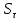 определяют по формулам
определяют по формулам
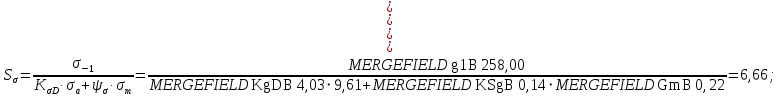
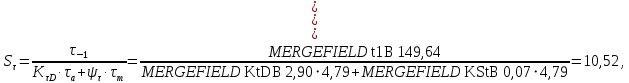
где
 и
и  – коэффициенты запаса прочности по нормальным и касательным напряжениям.
– коэффициенты запаса прочности по нормальным и касательным напряжениям.Суммарный коэффициент запаса прочности
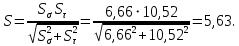
Условие прочности вала имеет вид
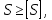
где [S] – допускаемый коэффициент запаса прочности.
Рекомендуемое значение
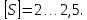
Усталостная прочность вала в сечении В обеспечена.
3.4 Расчет тихоходного вала в сечении С
1) Определение нагрузок
Суммарный изгибающий момент
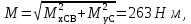
где MхСВ- изгибающий момент в горизонтальной плоскости,
Крутящий момент Тт = 1153,63 Нм,
Осевая сила Fa= 1,225 кН.
2) Геометрические характеристики опасного сечения
В сечении С имеется шпоночный паз со следующими размерами:
b=24 мм, t1=9 мм,
где b – ширина; t1– глубина шпоночного паза на валу.
Значения площади поперечного сечения A, осевого
 и полярного
и полярного  моментов сопротивлений для типовых поперечных сечений определяют по формулам.
моментов сопротивлений для типовых поперечных сечений определяют по формулам.Осевой момент сопротивления:
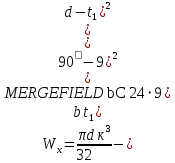
Полярный момент сопротивления:

Площадь сечения:
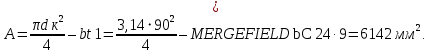
3) Определение напряжений
Напряжения изгиба меняются по симметричному циклу с амплитудой:
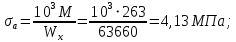
Средние нормальные напряжения:
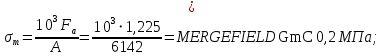
Касательные напряжения меняются по отнулевому циклу:
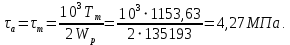
4) Пределы выносливости
Пределы выносливости материала при симметричном цикле изгиба и кручения определяются по следующим формулам:
для углеродистых сталей:
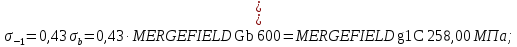
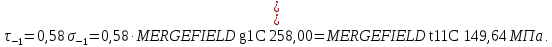
здесь
 – предел прочности материала вала
– предел прочности материала вала5) Эффективные коэффициенты концентрации напряжений и коэффициенты влияния размера поперечного сечения.
В опасном сечении имеется 2 концентратора напряжений: посадка с натягом и шпоночный паз.
Для посадки с натягом
 определяется из Табл. 7,5
определяется из Табл. 7,5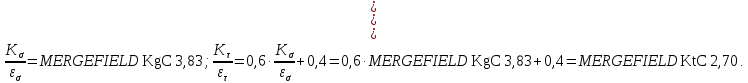
Эффективные коэффициенты концентрации напряжений для шпоночного паза:
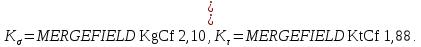
Коэффициенты влияния размера поперечного сечения:
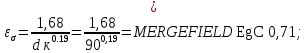
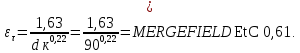
Для шпоночного паза:
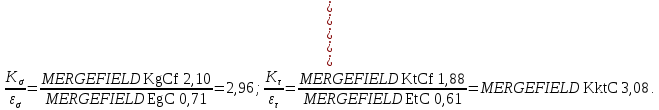
Выбираем наибольшие значения между значениями посадки с натягом и шпоночным пазом:
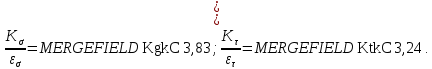
6) Коэффициент влияния шероховатости поверхности.
Поверхность вала под подшипник получена чистовым обтачиванием с
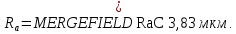
KF – коэффициент влияния шероховатости поверхности, определяется в зависимости от
 KF=3,21.
KF=3,21. 7) Коэффициент чувствительности к асимметрии цикла,
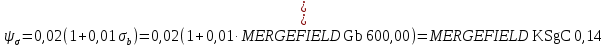 ;
; 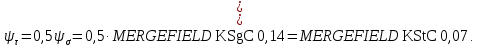
8) Коэффициент влияния упрочнения.
Примем, что на участке вала с опасным сечением упрочнение отсутствует.
KV– коэффициент влияния упрочнения, KV=1.
9) Коэффициенты перехода от пределов выносливости образца к пределам выносливости детали.
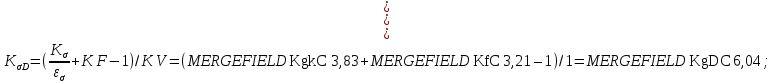
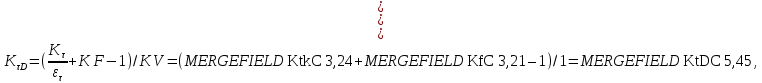
где
 и
и  – эффективные коэффициенты концентрации напряжений
– эффективные коэффициенты концентрации напряжений