Файл: Образец выполнения практического задания 1 Запишем исходные данные расчетной электрической цепи постоянного тока.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 14
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Образец выполнения практического задания 1
Запишем исходные данные расчетной электрической цепи постоянного тока.
Источник входного напряжения (рис. 3):

Рис. 3. Источник входного напряжения
Нагрузка (рис. 4)
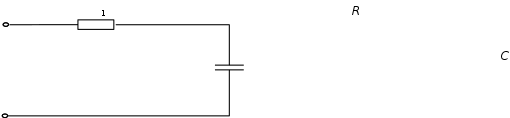
Рис. 4. Нагрузка
Сопротивление резистора:
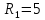 Ом,
Ом, 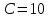 мкФ. Значения источника электрической энергии:
мкФ. Значения источника электрической энергии: 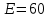 В,
В, 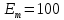 В,
В, 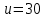 0,
0, 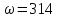 рад/с.
рад/с. Объединим схемы на рисунках 3 и 4 в одну (рис. 5).
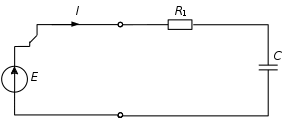
Объединим схемы на рисунках 3 и 4 в одну (рис. 5).Рис. 5. Исходная схема для расчета цепи
Проанализируем исходную схему (рис. 5). До коммутации к нагрузке было подключено постоянное напряжение Е. В момент коммутации ключ из положения 1 переключается в положение 2 на источник переменного напряжение e(t). Через нагрузку начинает протекать переменное напряжение.
 Найдем докоммутационные значения токов и напряжений. До коммутации источник переменного напряжения отключен от цепи, поэтому можно его временно удалить из схемы (рис. 6).
Найдем докоммутационные значения токов и напряжений. До коммутации источник переменного напряжения отключен от цепи, поэтому можно его временно удалить из схемы (рис. 6).Рис. 6. Докоммутационная схема для расчета цепи
Анализ схемы (рис. 6) показывает, что электрическая цепь содержит всего 1 контур. В этом контуре присутствуют источник постоянного напряжения E, активное сопротивление R1 и емкость С. На постоянном токе емкостное сопротивление равно бесконечности. Бесконечность – это разрыв в цепи (рис. 7). Получается, что ток в цепи будет равен нулю.
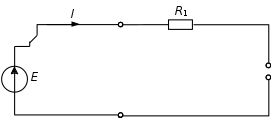
Рис. 7. Упрощенная докоммутационная схема для расчета цепи
Если ток в цепи нулевой, тогда, согласно закону Ома, напряжение на сопротивлении
R1 (формула 1):
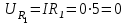 (В). (1)
(В). (1)Тогда получается, согласно 2 закону Кирхгофа, что все входное напряжение приложено к конденсатору.
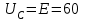 (В). (2)
(В). (2)Запишем данные в таблицу 4.
Таблица 4
| i(0-) | uR1(0-) | uC(0-) |
| 0 | 0 | 60 |
Независимыми начальными значениями являются ток в катушке индуктивности и напряжение на конденсаторе. В нашей схеме присутствует только конденсатор. Значит, независимым начальным значением будет только напряжение на конденсаторе (формула 3):
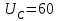 (В). (3)
(В). (3)Рассчитаем значения в момент коммутации при t = 0+. В момент коммутации ключ S переключается из положения 1 в положение 2 (рис. 5). При этом источник постоянного напряжения Е отключается и подключается источник переменного напряжения e(t). В результате упрощенная схема будет выглядеть, как на рисунке 8.
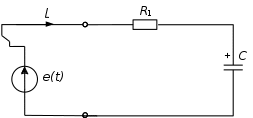
Рис. 8. Электрическая цепь в момент коммутации
Конденсатор до коммутации зарядился и имеет полярность, указанную на рис. 8. Для упрощения расчетов в момент коммутации конденсатор можно заменить на источник постоянного напряжения или же просто указывать напряжение на конденсаторе. Согласно закону коммутации, напряжение на конденсаторе скачком измениться не может (формула 4):
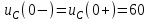 (В) (4)
(В) (4)Пусть ток в цепи будет протекать по часовой стрелке. Составим уравнение по 2 закону Кирхгофа и из него выразим ток в цепи i(0+) (формула 5):
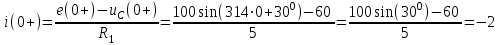 (А). (5)
(А). (5)Знак «-» у тока говорит, что на самом деле он протекает в противоположную сторону (против часовой стрелки).
Найдем напряжение на сопротивлении R1 (формула 6):
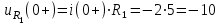 (В). (6)
(В). (6)Запишем данные в таблицу 5.
Таблица 5
| i(0+) | uR1(0+) | uC(0+) |
| -2 | -10 | 60 |
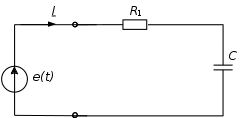 Рассчитаем значения в принужденном режиме. Это такой режим, когда ключ S переключился из положения 1 в положение 2 и прошло бесконечно большое время (рис. 9). Расчет напряжений и токов такой электрической цепи выполняется комплексным методом.
Рассчитаем значения в принужденном режиме. Это такой режим, когда ключ S переключился из положения 1 в положение 2 и прошло бесконечно большое время (рис. 9). Расчет напряжений и токов такой электрической цепи выполняется комплексным методом.Рис. 9. Электрическая цепь в момент коммутации
Запишем амплитудное комплексное значение напряжения источника ЭДС (формула 7):
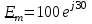 (В). (7)
(В). (7)Найдем значение емкостного сопротивления Xc (формула 8):
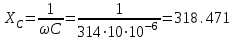 (Ом). (8)
(Ом). (8)Найдем амплитудное значение комплексного тока в цепи по закону Ома (формула 9):
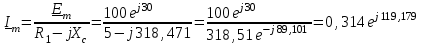 (А). (9)
(А). (9)Найдем амплитудное комплексное значение напряжения на сопротивлении по закону Ома (формула 10):
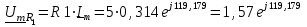 (В). (10)
(В). (10)Найдем амплитудное комплексное значение напряжение на емкости по закону Ома (формула 11):
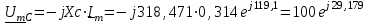 (А). (11)
(А). (11)Запишем данные в таблицу 6.
Таблица 6
Принужденные значения токов и напряжений
| Комплексные значения в принужденном режиме | ||
| Im | UmR1 | UmC |
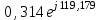 | 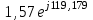 | 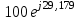 |
| Принужденные мгновенные значения | ||
| iпр(t) | uR1пр(t) | uCпр(t) |
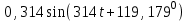 | 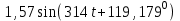 | 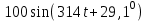 |
Найдем корни характеристического уравнения. Для этого рассмотрим послекоммутационную схему для свободного режима. В ней все источники ЭДС заменяются на перемычки, источники тока – на разрывы. Индуктивность заменяется на pL , емкость -
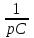 (рис. 10). В получившейся схеме выполним разрыв в любом месте и относительно этого разрыва рассчитаем характеристическое сопротивление цепи (рис 11).
(рис. 10). В получившейся схеме выполним разрыв в любом месте и относительно этого разрыва рассчитаем характеристическое сопротивление цепи (рис 11).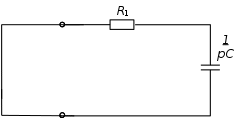
Рис. 10. Электрическая цепь для расчета корней

Рис. 11. Электрическая цепь с разрывом для расчета корней
В получившейся электрической цепи два сопротивления подключены последовательно (формула 12):
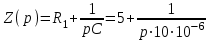 . (12)
. (12)Приравняем характеристическое сопротивление к нулю (формула 13) и найдем неизвестный корень p (формула 14):
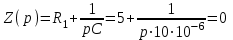 , (13)
, (13)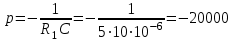 . (14)
. (14)Корень характеристического уравнения отрицательный, значит переходный процесс закончится.
Постоянная времени цепи (формула 15):
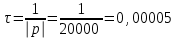 (c). (15)
(c). (15)Постоянная интегрирования в общем виде рассчитывается (формула 16):
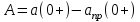 . (16)
. (16)Рассчитаем постоянные интегрирования для тока и напряжений (формулы 17-19):
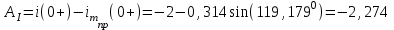 (А), (17)
(А), (17)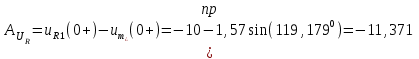 (В), (18)
(В), (18)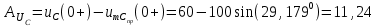 (В). (19)
(В). (19)Запишем значения свободных составляющих (формулы 20–22):
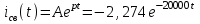 (А), (20)
(А), (20)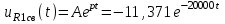 (В), (21)
(В), (21)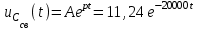 (В). (22)
(В). (22)Запишем зависимость изменения напряжений и токов от времени при переходном процессе как сумму свободной и принужденной составляющей с учетом значений до коммутации (формулы 23-25):
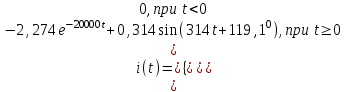 (А), (23)
(А), (23)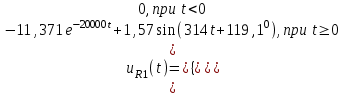 (В), (24)
(В), (24)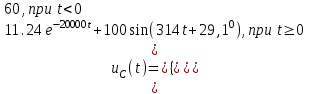 (В) . (25)
(В) . (25)Форма графика тока и графика напряжения на сопротивлении совпадает, поэтому график тока строить не будем. Он такой же по форме, как график напряжения на сопротивлении, только в R1 раз меньше. Построим графики напряжений на элементах от времени (рисунки 12 и 13). На 12 рисунке изображен укрупненно момент начала переходного процесса, На рисунке 13 изображен переходный процесс на интервале полупериода входного сигнала.
Из графиков видно, что выполняется закон коммутации. Напряжение на конденсаторе скачком не изменилось, а ток через конденсатор по форме совпадает с напряжением на резисторе, изменяется скачком.
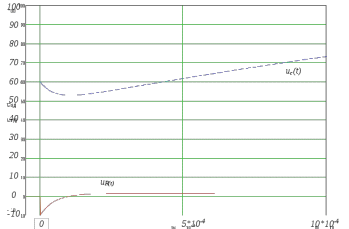
Рис. 12. Графики зависимости напряжения на сопротивлении и на емкости от времени
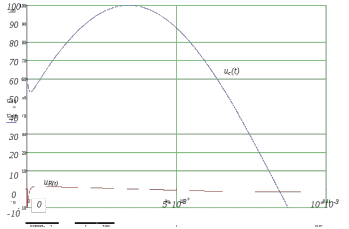
Рис. 13. Графики зависимости напряжения на сопротивлении и на емкости от времени на интервале полупериода входного сигнала