ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.04.2024
Просмотров: 199
Скачиваний: 0
Объемный подход
В двоичной системе счисления знаки 0 и 1 будем называть битами(от английского выраженияBinarydigiTs- двоичные цифры). В компьютере бит является наименьшей возможной единицей информации. Объем информации, записанной двоичными знаками в памяти компьютера или на внешнем носителе информации подсчитывается просто по количеству требуемых для такой записи двоичных символов. При этом, в частности, невозможно нецелое число битов (в отличие от вероятностного подхода).
Для удобства использования введены и более крупные, чем бит, единицы количества информации. Так, двоичное слово из восьми знаков содержит один, байтинформации,1024 байта образуюткилобайт(кбайт), 1024 килобайта -мегабайт(Мбайт), а 1024 мегабайта -гигабайт(Гбайт).
Между вероятностным и объемным количеством информации соотношение неоднозначное. Далеко не всякий текст, записанный двоичными символами, допускает измерение объема информации в кибернетическом смысле, но заведомо допускает его в объемном. Далее, если некоторое сообщение допускает измеримость количества информации в обоих смыслах, то они не обязательно совпадают, при этом кибернетическое количество информации не может быть больше объемного.
1.4. Свойства информации
Информацию следует считать особым видом ресурса, при этом имеется ввиду толкование «ресурса» как запаса неких знаний материальных предметов или энергетических, структурных или каких-либо других характеристик предмета. В отличие от ресурсов, связанных с материальными предметами, информационные ресурсы являются неистощимыми и предполагают существенно иные методы воспроизведения и обновления, чем материальные ресурсы.
Рассмотрим некоторый набор свойств информации:
• запоминаемость;
• передаваемость;
• преобразуемость;
• воспроизводимость;
• стираемость.
Свойство запоминаемости- одно из самых важных. Запоминаемую информацию будем называть макроскопической (имея ввиду пространственные масштабы запоминающей ячейки и время запоминания). Именно с макроскопической информацией мы имеем дело в реальной практике.
Передаваемостьинформации с помощью каналов связи (в том числе с помехами) хорошо исследована в рамках теории информации К. Шеннона. В данном случае имеется ввиду несколько иной аспект - способность информации к копированию, т.е. к тому, что она может быть «запомнена» другой макроскопической системой и при этом останется тождественной самой себе. Очевидно, что количество информации не должно возрастать при копировании.
Воспроизводимостьинформации тесно связана с ее передаваемостью и не является ее независимым базовым свойством. Если передаваемость означает, что не следует считать существенными пространственные отношения между частями системы, между которыми передается информация, то воспроизводимость характеризует неиссякаемость и неистощимость информации, т.е. что при копировании информация остается тождественной самой себе.
Фундаментальное свойство информации - преобразуемость.Оно означает, что информация может менять способ и форму своего существования. Копируемость есть разновидность преобразования информации, при котором ее количество не меняется. В общем случае количество информации в процессах преобразования меняется, но возрастать не может. Свойство стираемостиинформации также не является независимым. Оно связано с таким преобразованием информации (передачей), при котором ее количество уменьшается и становится равным нулю.
§ 2. Алгоритм и его свойства
2.1. Различные подходы к понятию «алгоритм»
Понятие алгоритма - одно из фундаментальных понятий информатики. Алгоритмизация наряду с моделированием выступает в качестве общего метода информатики. К реализации определенных алгоритмов сводятся процессы управления в различных системах, что делает понятие алгоритма близким и кибернетике.
Алгоритмы являются объектом систематического исследования пограничной между математикой и информатикой научной дисциплины, примыкающей к математической логике - теории алгоритмов.
Особенность положения состоит в том, что при решении практических задач, предполагающих разработку алгоритмов для реализации на ЭВМ, и тем более при использовании на практике информационных технологий, можно, как правило, не опираться на высокую формализацию данного понятия. Поэтому представляется целесообразным познакомиться с алгоритмами и алгоритмизацией на основе содержательного толкования сущности понятия алгоритма и рассмотрения основных его свойств. При таком подходе алгоритмизация более выступает как набор определенных практических приемов, особых специфических навыков рационального мышления в рамках заданных языковых средств. Можно провести аналогию между этим обстоятельством и рассмотренным выше подходом к измерению информации: тонкие математические построения при «кибернетическом» подходе не очень нужны при использовании гораздо более простого «объемного» подхода при практической работе с компьютером.
Само слово «алгоритм» происходит от algorithmi - латинской формы написания имени великого математика IX века аль-Хорезми, который сформулировал правила выполнения арифметических действий. Первоначально под алгоритмами и понимали только правила выполнения четырех арифметических действий над многозначными числами.
2.2. Понятие исполнителя алгоритма
Понятие исполнителя невозможно определить с помощью какой-либо формализации. Исполнителем может быть человек, группа людей, робот, станок, компьютер, язык программирования и т.д. Важнейшим свойством, характеризующим любого из этих исполнителей, является то, что исполнитель умеет выполнять некоторые команды. Так, исполнитель-человек умеет выполнять такие команды как «встать», «сесть», «включить компьютер» и т.д., а исполнитель-язык программирования Паскаль - команды WRITE,END,READи другие аналогичные. Вся совокупность команд, которые данный исполнитель умеет выполнять, называется системой команд исполнителя(СКИ).
В качестве примера (рис. 2.1) рассмотрим исполнителя-робота, работа которого состоит в собственном перемещении по рабочему полю (квадрату произвольного размера, разделенному на клетки) и перемещении объектов, в начальный момент времени находящихся на «складе» (правая верхняя клетка).
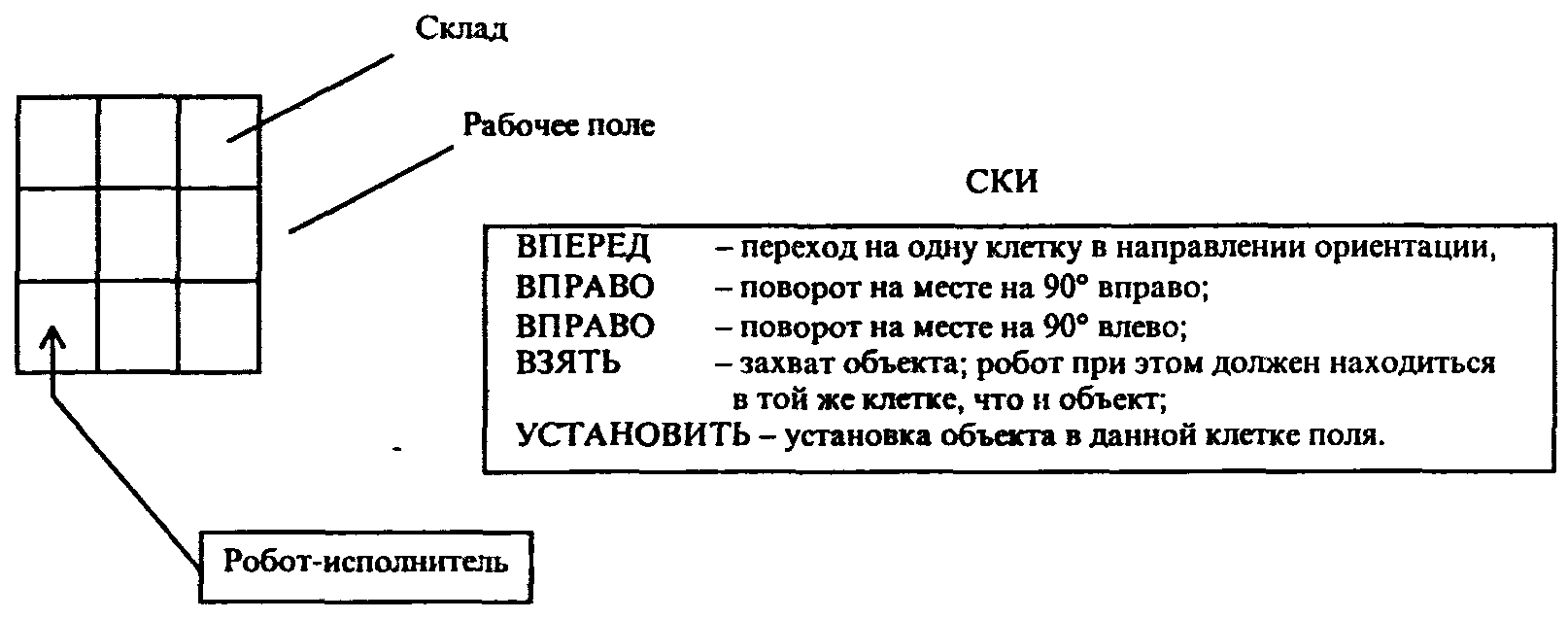
Рис. 2.1. Исполнитель-робот
Одно из принципиальных обстоятельств состоит в том, что исполнитель не вникает в смысл того, что он делает, но получает необходимый результат. В таком случае говорят, что исполнитель действует формально,т. е. отвлекается от содержания поставленной задачи и только строго выполняет некоторые правила, инструкции.
Это - важная особенность алгоритмов. Наличие алгоритма формализует процесс решения задачи, исключает рассуждение исполнителя. Использование алгоритма дает возможность решать задачу формально, механически исполняя команды алгоритма в указанной последовательности. Целесообразность предусматриваемых алгоритмом действий обеспечивается точным анализом со стороны того, кто составляет этот алгоритм.
Введение в рассмотрение понятия «исполнитель» позволяет определить алгоритм как понятное и точное предписание исполнителю совершить последовательность действий, направленных на достижение поставленной цели. В случае исполнителя-робота мы имеем пример алгоритма «в обстановке», характеризующегося отсутствием каких-либо величин. Наиболее же распространенными и привычными являются алгоритмы работы с величинами - числовыми, символьными, логическими и т.д.
2.3. Графическое представление алгоритмов
Алгоритм, составленный для некоторого исполнителя, можно представить различными способами: с помощью графического или словесного описания, в виде таблицы, последовательностью формул, записанным на алгоритмическом языке (языке программирования). Остановимся на графическом описании алгоритма, называемом блок-схемой. Этот способ имеет ряд преимуществ благодаря наглядности, обеспечивающей, в частности, высокую «читаемость» алгоритма и явное отображение управления в нем.
Прежде всего определим понятие блок-схемы. Блок-схема - это ориентированный граф, указывающий порядок исполнения команд алгоритма; вершины такого графа могут быть одного из трех типов (рис. 2.2).
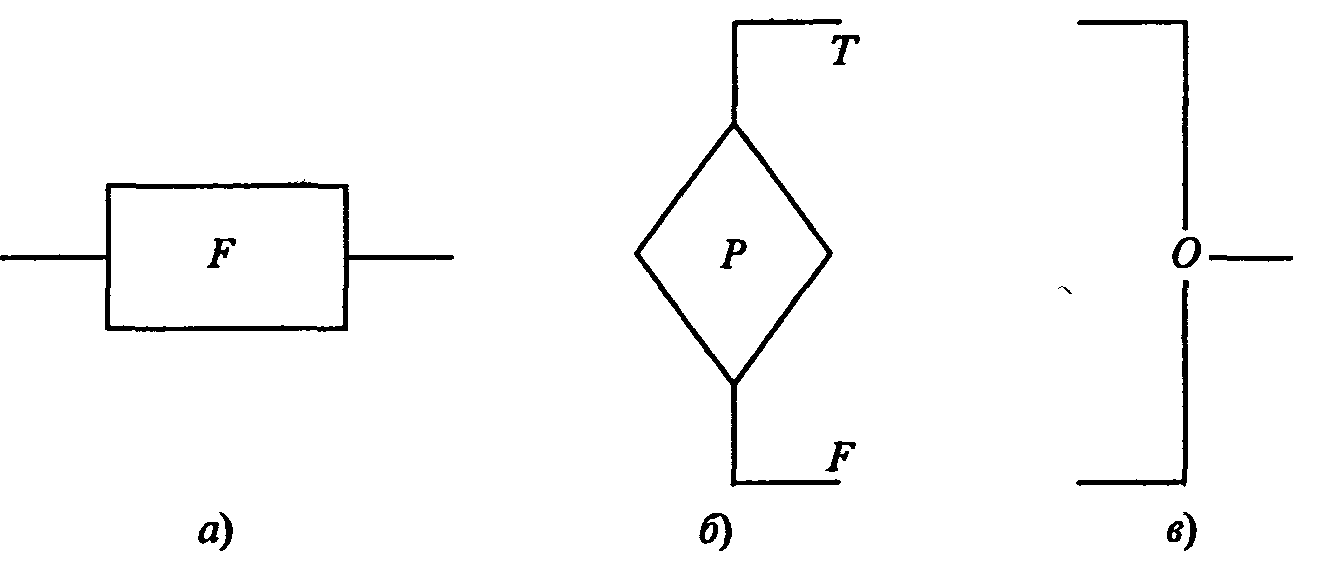
Рис.2.2. Три типа вершин графа
На рис. 2.2 изображены «функциональная» (a) вершина (имеющая один вход и один выход); «предикатная»(б)вершина, имеющая один вход и два выхода (в этом случае функцияРпередает управление по одной из ветвей в зависимости от значенияР (Т,т.е.true, означает «истина»,F,т.е.false- «ложь»); «объединяющая» (в) вершина (вершина «слияния»), обеспечивающая передачу управления от одного из двух входов к выходу. Иногда вместо Т пишут «да» (либо знак +), вместоF-«нет» (либо знак -).
Из данных элементарных блок-схем можно построить три блок-схемы, имеющих особое значение для практики алгоритмизации.
Следование- самая важная из структур. Она означает, что действия могут быть выполнены друг за другом:
![]()
Рис. 2.3.Структура «следование»
Эти прямоугольники могут представлять как одну единственную команду, так и множество операторов, необходимых для выполнения сложной обработки данных.
Ветвление- это структура, обеспечивающая выбор между двумя альтернативами. Выполняется проверка, а затем выбирается один из путей.
Эта структура называется также «ЕСЛИ - ТО - ИНАЧЕ», или «развилка». Каждый из путей (ТО или ИНАЧЕ) ведет к общей точке слияния, так что выполнение программы продолжается независимо от того, какой путь был выбран.
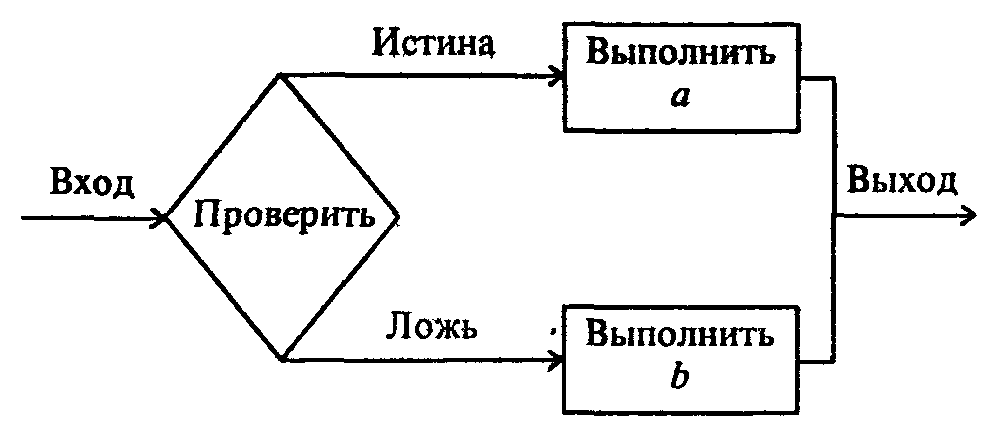
Рис. 2.4.Структура «ветвление»
Может оказаться, что для одного из результатов проверки ничего предпринимать не надо. В этом случае можно применять только один обрабатывающий блок: