Файл: Численные методы.doc

6. Метод наименьших квадратов обработки экспериментальных данных.

Пусть в результате измерений в процессе некоторого опыта получена таблица некоторой зависимости

х	x0	x1	…	xn
y=f(x)	y0	y1	…	yn

Нужно найти формулу, выражающую эту зависимость аналитически (то есть в виде уравнения). Поставим задачу так, чтобы с самого начала обязательно учитывался характер исходной функции, то есть требуется найти функцию заданного вида (1), которая в точкахпринимает значения как можно более близкие к табличным значениям. Практически вид, приближающей функцииможно определить, например, следующем образом. По таблице строиться точечный график функции, затем проводится плавная кривая по возможности наилучшим образом, отражающая характер расположения . По полученной прямой таким образом кривой устанавливается вид приближенной функции. Обычно вид берут из числа простых аналитических функций. Следует заметить, что строгая функциональная зависимость для экспериментально полученной таблицы наблюдается редко, так как каждая из участвующих в ней величин может зависеть от многих случайных факторов. Формула (1) называетсяэмпирической

формулой или уравн регрессии. Следует заметить, что формула (1) интересна тем, что позволяет находить значения функции для нетабличных значенийх , «сглаживает» результаты измерений величины у. Оправданность такого подхода определяется в конечном счете практической полезностью наилучшей формулы.

---

Метод наименьших квадратов.Предположим, что приближенная функция в точкахимеет значения(2) требование близости табличных значенийи значений (2) и можно истолковать следующим образом. Будем рассматривать совокупность значений функциииз таблицы и совокупность значений (2) как координаты 2-х точекп-мерного пространства, тогда задача приближения функции может быть переформулирована следующем образом. Найдем такую функцию , чтобы расстояние между точкамибыло минимальным. Воспользуемся метрикой евклидова пространства и приходим к требованию, чтобы величина

(3)

была наименьшей, что равносильно следующему

(4)

Должна быть минимальной.

Таким образом, задача приближения функции формулируется следующем образом: найти функцию определенного вида, так чтобы сумма квадратов (4) была наименьшей. Такая задача носит название риближения функции методом наименьших квадратов.

Задача 6.1.Стационарное распределение температуры в теплоизолированном тонком стержне описывается линейной функцией. Дана таблица измеренных температур в соответствующих точках стержня:

Х	0	2	6	8	10	14	16	20
У	32	29,2	23,3	19,9	17,2	11,3	7,8	2

---

Методом наименьших квадратов найти эту функцию. Оцените качество полученного приближения.

Решениe:(в таблице вместо игрик с + ставьте игрик с волнистой чертой)

i	x		xy	x^2	=F(x)
1	0	32	0	0	32,19	-0,19	0,0361
2	2	29,2	58,4	4	29,17	0,03	0,0009
3	6	23,3	139,8	36	23,13	0,17	0,0289
4	8	19,9	159,2	64	20,11	-0,21	0,0441
5	10	17,2	172	100	17,09	0,11	0,0121
6	14	11,3	158,2	196	11,05	0,25	0,0625
7	16	7,8	124,8	256	8,03	-0,23	0,0529
8	20	2	40	400	1,99	0,01	0,0001
	76	142,7	852,4	1056

---

M_x==9,5 M_x^2==132

M_y=17,84

M_xy=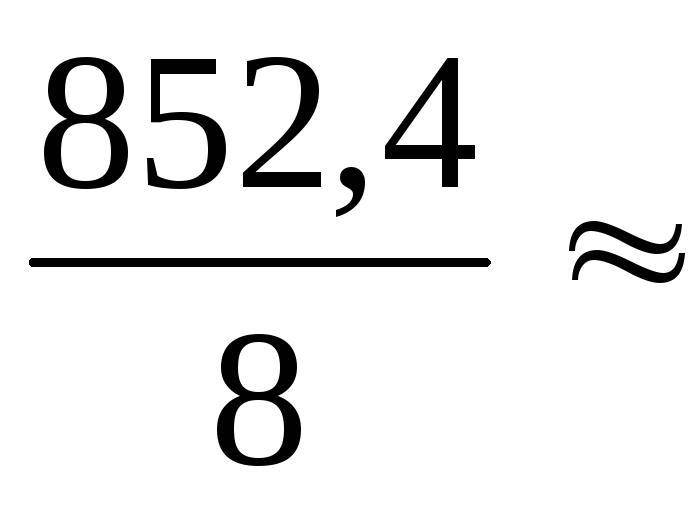106,55

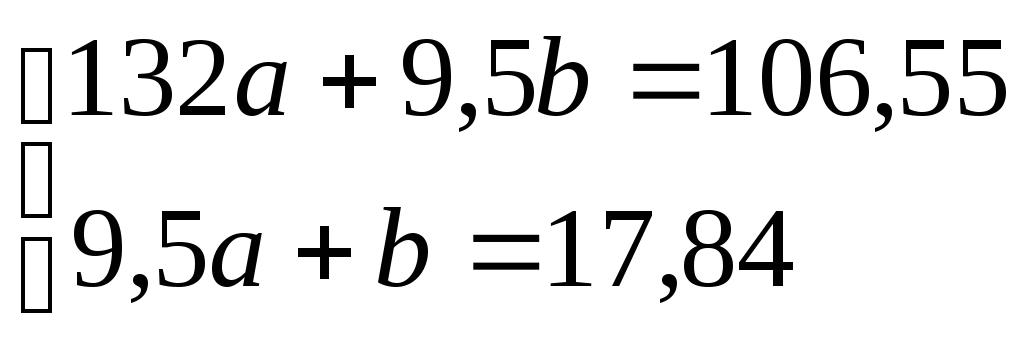
b=17,84

132a

a=

b=

уравнение прямой:

Оценим качество полученного приближения, для этого найдём сумму квадратов отклонений:

, т.о. получаем сумму квадратов отклонений .Полученное приближение не является наилучшим.

Задача 6.2. Методом наименьших квадратов подобрать показательную функцию по следующим табличным данным:

Х	2,2	2,7	3,5	4,1
У	67	60	53	50

Решение: приближающую функцию будем искать в виде:

,

---

пролагорифмируем:

Обозначим:

,,m=A

Составим таблицу, в которой будем оформлять расчеты:

x	z	xz	x	^(-0,152x)		^2
2,2	4,205	9,251	4,84	65,783	1,267	1,605
2,7	4,094	11,054	7,29	60,923	-0,923	0,852
3,5	3,970	13,895	12,25	53,947	-0,947	0,897
4,1	3,912	16,039	16,81	49,245	0,755	0,57
12,5	16,181	50,239	41,19

M_x=3,125 M_xz=12,56

M_z=4,045 M_x^2=10,298

Для нахождения A и B получаем след. систему:

---