Файл: Численные методы.doc

Последовательность точек

, , …,, … (3)

называется итерационной последовательность п-мерного пространства. При определенных условиях (рассмотрим их ниже) эта может оказаться сходящейся и её придел будет являться решением системы (2).

Условие сходимости(в книги оно написано как необходимое, а в формулировке вопроса задается как достаточное , поэтому я вообще не стала указывать какре оно) модули диагональных коэффициентов системы (1) должны быть значительно больше модулей недиагональных коэффицентов этой системы.

---

4.1 Методом простой итерации решить слау с точностью 0.001.

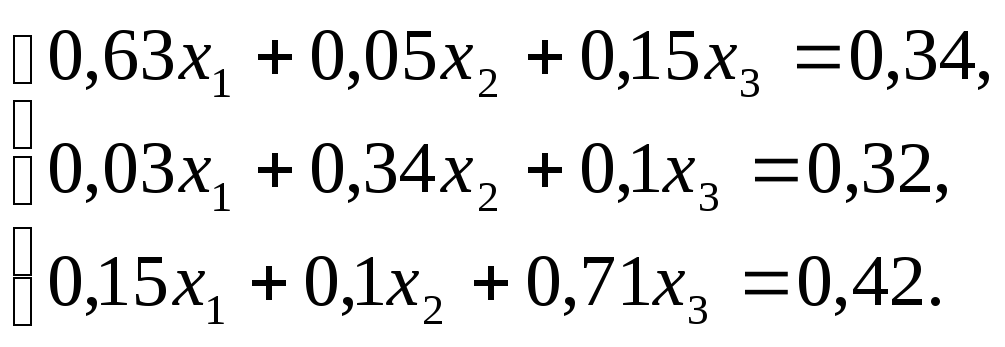
Решение:

Необходимое условие выполнено, коэффициенты на главной диагонали по модулю больше, чем все остальные.

Приведем систему к виду

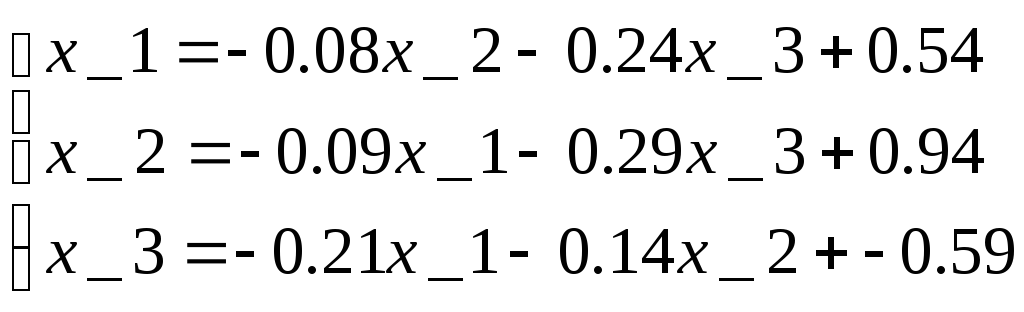
Проверим достаточное условие сходимости итерационного процесса по строкам:

То есть максимум сумм модулей коэффициентов при неизвестных, взятых по строкам, должны быть меньше единицы

0.08+0.24=0.32<1

0.09+0.29=0.38

0.21+0.14=0.35

Критерий окончания вычислений находим по формуле

где

получим

За нулевое приближение примем столбец свободных членов

Корни ищем по формуле

Другими словами, на каждом этапе к=1,2, ……, мы будем вести подсчеты по системе

Все вычисления для удобства записываем в таблицу

k	x_1	x_2	x_3
0 1 2 3 4 5 6 7	0.54 0.32 0.4 0.37 0.384 0.38 0.3813 0.3808	0.94 0.72 0.81 0.78 0.7936 0.7885 0.7903 0.7898	0.59 0.35 0.42 0.39 0.4031 0.3983 0.3998 0.3993

---

к=1:

х_1=0.54-0.08*0.94-0.24*0.59=0.32

х_2=0.094-0.09*0.54-0.29*0.59=0.72

х_3=0.59-0.21*0.54-0.14*.94=0.35

и так далее до к=7, на к=7 точность будет достигнута.

При к=7 будут полученные следующие ответы

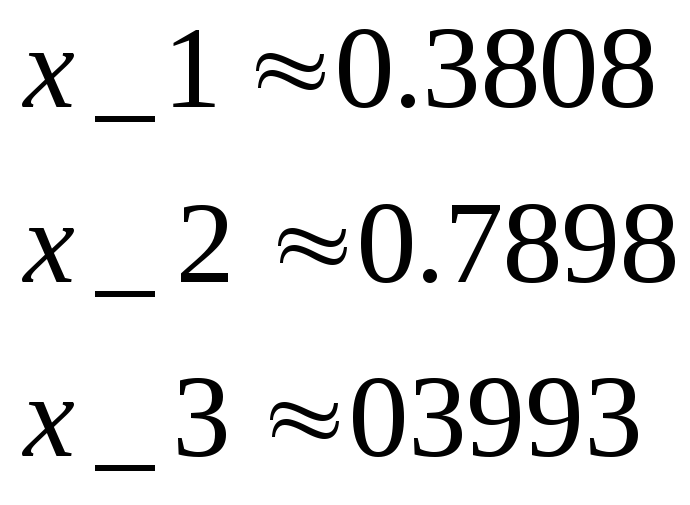
5. Интерполяционная формула Лагранжа и оценка её погрешности.

Задача интерполирования заключается в следующем: известны значения некоторой функции, образующ следующую таблицу

х	x0	x1	…	xn
y=f(x)	y0	y1	…	yn

И ищется функция F(x) приблизительно равная исходной и значения которой в точках х_0……х_п совпадают со значениями исходной в этих точка то есть .(*)

х_0……х_п называются узлами интерполирования. Рассмотрим случай, когда интерпол-ю F(x) находится в виде многочлена степени не выше п.

Интерполяционная формула Лагранжа и оценка её погрешности.

Пусть f задана таблицей. Построим интерполяц-й многочлен степени не вышеп , для которого выполняется (*). Будем искать в виде(2)

где - многочлен степенип, причем

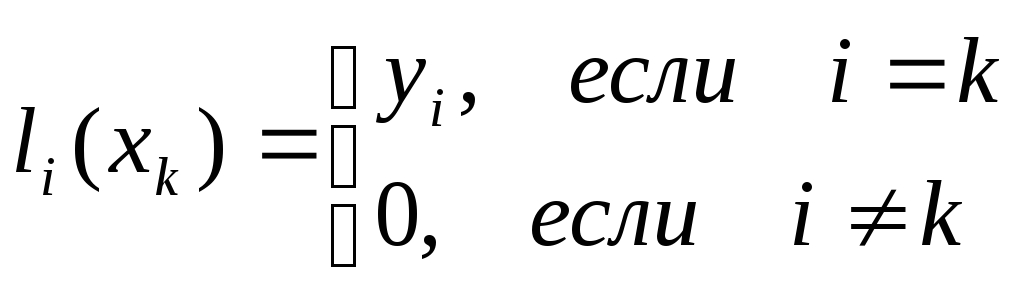(3)

Очевидно, что (3) с учетом (2) вполне обеспечит выполнение условий (*). Многочлен составим следующем образом

(4)

где - постоянный коэффициент, значение которого находится из первой части условия (3):

---

.

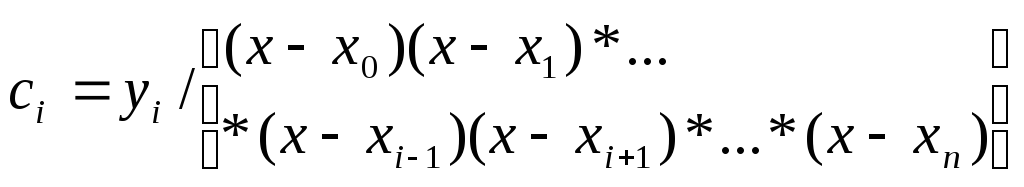Заметим, что ни один множитель знаменателя не равен 0. Подставив последнее выражение в (4) и далее с учетом (2) окончнательно получим интерполяционный многочлен Лагранжа:

или

(5)

Разность между исходной функцией и интерполяционным многочленом есть остаточный член интерполяц многочлена, который имеет вид

В силу единственности многочлена интерполир-я, этот остаточный член будет являться погрешностью. Оценка погрешности будет иметь вид

где

Задача 5.1. Дана таблица значений функции:

Х	1,2	1,9	3,3	4,7
f(x)	0,3486	1,0537	1,7844	2,2103

Вид функции: .

Найти значение этой функции в точке x = 4, пользуясь интерполяционным многочленом Лагранжа. Оценить погрешность. Результат интерполирования сравнить с вычислением значения функции по её выражению.

Решение: по формуле

ищем первые три значения в точке х=4.

=+++=

---

=0,06972-0,52685+1,7844+0,66309=1,99036

Погрешность вычисляем по формуле

==

=

---