Файл: Тема 10.doc

,

отсюда следует:

,

(10.11)

где

первый член прогрессии.

Зная , мы точно можем определить, какую тенденцию развития явления имеет геометрическая последовательность. Формула (10.11) является средней геометрической и применяется в случае, когда определяющий показатель является не суммой значений, а их произведением. Следовательно, если варианты связаны между собой не знаком сложения, а знаком произведения, нужно вычислить среднюю геометрическую. Обычно средний темп роста вычисляется по формуле средней геометрической из цепных коэффициентов роста:

.

(10.12)

Так как всякий темп роста является отношением уровней ряда динамики, то в формуле ,…, средней геометрической темпы роста заменяются соответствующим отношением уровней. Заменив темпы роста выражающими их отношениями и, приняв во внимание, что эти величины перемножаются, найдем подкоренное выражение:

Следовательно, средний темп роста может быть выражен формулой:

.

(10.13)

При расчете средних темпов роста по периодам различной продолжительности (разноотстоящие ряды динамики) пользуются средними геометрическими взвешенными по продолжительности периодов. Формула средней геометрической взвешенной будет иметь вид:

.

(10.14)

---

где		интервал, в течение которого сохраняется данный темп роста;
		сумма отрезков периода.

Средний темп прироста не может быть определен на основании последовательных темпов прироста или показателей среднего абсолютного прироста. Для его вычисления необходимо вначале найти средний темп роста, а затем уменьшить его на единицу, или 100%.

.

(10.15)

Для проведения глубокого анализа динамики социально-экономических явлений следует параллельно использовать показатели скорости и интенсивности изменения уровней. Анализ, основанный на использовании какого-либо одного из этих показателей, неизбежно будет иметь односторонний характер.

Для комплексного статистического анализа необходимо использовать систему показателей, характеризующих абсолютную скорость и интенсивность изменения уровней ряда (рис. 10.2).

---

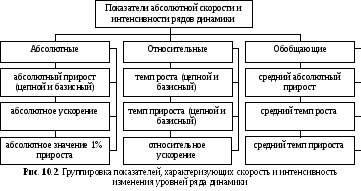
10.4 Компоненты ряда динамики

Ряд динамики может быть подвержен влиянию факторов эволюционного и осциллятивного характера, а также находиться под влиянием факторов разного воздействия.

Влияния эволюционного характера - это изменения, определяющие некое общее направление развития, как бы многолетнюю эволюцию, которая пробивает себе дорогу через другие систематические и случайные колебания. Такие изменения динамического ряда называются тенденцией развития, илитрендом.

Влияния осциллятивного характера - это циклические (конъюнктурные) исезонные колебания. Циклические (или периодические) состоят в том, что значение изучаемого признака в течение какого-то времени возрастает, достигает определенного максимума, затем понижается, достигает определенного минимума, вновь возрастает до прежнего значения и т.д. Иначе циклические колебания можно схематически представить в виде синусоиды. Циклические колебания в экономических процессах примерно соответствуют так называемым циклам конъюнктуры. Сезонные колебания - это колебания, периодически повторяющиеся в некоторое определенное время каждого года, дня месяца или часа дня. Эти изменения отчетливо наблюдаются на графиках многих рядов динамики, содержащих данные за период не менее одного года.

Наконец, рассмотрим нерегулярные колебания, которые для социально-экономических явлений можно разделить на две группы:

• спорадически наступающие изменения (появляющиеся от случая к случаю, не повсеместные, непериодические), вызванные, например, войной или экологической катастрофой;

• случайные колебания, являющиеся результатом действия большого количества относительно слабых второстепенных факторов.

Следовательно, первоначальные значения ряда динамики подвергаются самым разнообразным воздействиям. Выделим его четыре основные компоненты:

• основную тенденцию (тренд) ();

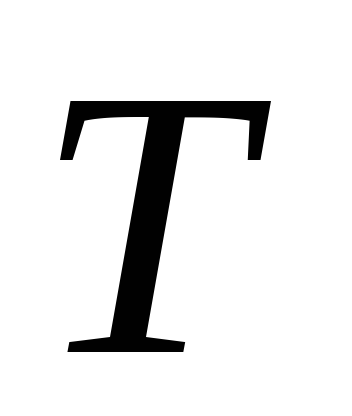• циклическую, или конъюнктурную ();

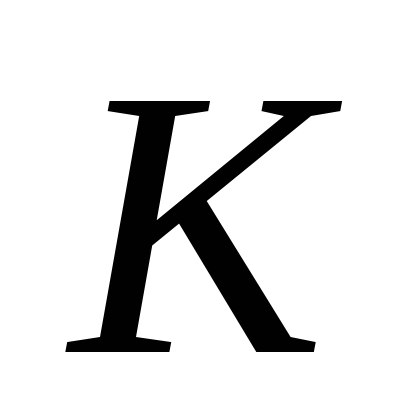• сезонную ();

• случайные колебания ().

---

Если ряд динамики разбить на различные компоненты, то он представляется в следующем виде:

.

В зависимости от взаимосвязи этих компонент между собой может быть построена аддитивная или мультипликативная модель ряда динамики.

Аддитивная модель ряда динамики характеризуется главным образом тем, что характер циклических и сезонных флюктуации (колебаний) остается постоянным (рис. 10.3).

Мультипликативная модель ряда динамики. В этой модели характер циклических и сезонных флюктуации оста­ется постоянным только по отношению к тренду (рис. 10.4).

10.5 Виды трендовой компоненты и проверка гипотезы о существовании тенденции

Тренд - это долговременная компонента ряда динамики. Она характеризует основную тенденцию развития явления, при этом остальные компоненты рассматриваются только как мешающие процедуре его определения. При наличии ряда наблюдаемых значений для различных моментов времени следует найти подходящую трендовую кривую, которая сгладила бы остальные колебания.

Виды основной тенденции. В социально-экономических рядах динамики можно наблюдатьтенденцию трех видов:

• среднего уровня;

• дисперсии;

• автокорреляции.

Тенденция среднего уровня аналитически выражается с помощью математической функции, вокруг которой варьируют фактические уровни исследуемого явления. В таком случае значения тренда в отдельные моменты времени будут являться математическим ожиданием ряда динамики. Часто тенденция среднего уровня называетсядетерминированной составляющей исследуемого явления, и соответствующий ряд динамики выражается следующим уравнением:

.

(10.16)

Тенденция дисперсии представляет собой тенденцию изменения отклонений между эмпирическими уровнями и детерминированной компонентой ряда.

---

Тенденция автокорреляции характеризует изменения связи между отдельными уровнями ряда динамики. Графически это изменение не прослеживается. Однако прежде чем перейти к выделению тренда, следует проверить гипотезу о том, существует ли он вообще. Отсутствие основной тенденции (тренда) означает неизменность среднего уровня ряда во времени.

Методы выявления наличия тенденции.В настоящее время для проверки наличия тренда известно около десятка критериев, различающихся как по мощности, так и по сложности математического аппарата. Рассмотрим два из них: метод, основанный на проверке разности средних двух разных частей одного и того же ряда, и метод Фостера-Стюарта.

Метод проверки существенности разности средних основан на-критерии Стьюдента. Ряд динамики разбивается на две равные или почти равные части. Проверяется гипотеза о существовании разно­сти средних:.

Воспользуемся методом проверки, разработанным для малых выборок, так как число членов анализируемого ряда, как правило, довольно незначительно. За основу проверки берется -критерий Стьюдента. При гипотеза об отсутствии тренда отвергается, при гипотеза () принимается. Здесь- расчетное значение, найденное для анализируемых данных,- табличное значение этого критерия при уровне вероятности ошибки, равном. В случае равенства или при несущественном различии дисперсий двух исследуемых совокупностей () исчисляется отношение средних с помощью выражения:

,

(10.17)

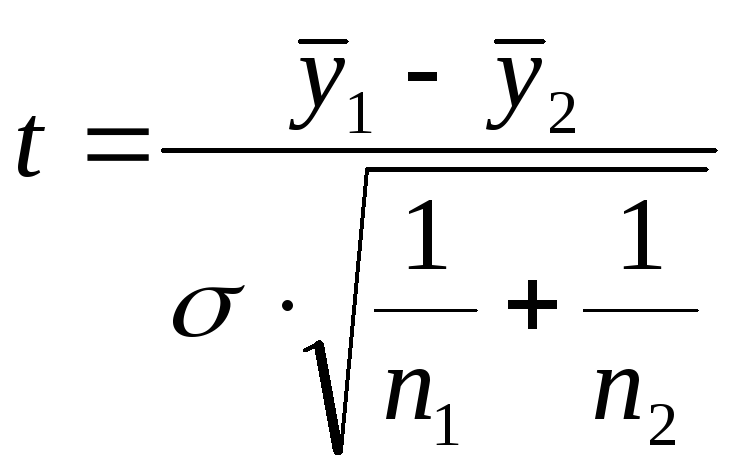где	и	средние для первой и второй половины ряда динамики;
	и	число наблюдений в этих частях ряда;
		среднее квадратическое отклонение разности средних.

---