Файл: Тема 10.doc

Значение берется с числом степеней свободы, равным. Необходимое значениеможно определить на основе средней взвешенной величины дисперсий отдельных совокупностей:

.

(10.18)

При оценивании дисперсий для первой и второй частей ряда динамики ивозьмем число степеней свободы, равноеисоответственно:

.

Проверка гипотезы о равенстве дисперсий реализуется с помощью -критерия, который основан на сравнении расчетного отноше­ния с табличным.

,

(10.19)

где

.

Если расчетное значение меньше, чем табличное, при заданном уровне вероятности, то можно принять гипотезу о равенстве дисперсий. Если же больше, чем табличное значение, то гипотеза о равенстве дисперсий отклоняется и формула (10.17) для испытания разности средних не может быть применена.

Следует заметить, что данный метод дает вполне приемлемые результаты лишь в случае рядов с монотонной тенденцией. Когда же ряд динамики меняет общее направление развития, то точка поворота тенденции оказывается близкой к середине ряда, поэтому средние двух отрезков будут близки, а проверка может не показать наличие тенденции.

---

Метод Фостера-Стюарта кроме определения наличия тенденции явления позволяет выявить основную тенденцию дисперсии уровней ряда динамики, что важно знать при анализе и прогнозировании экономических явлений.

Расчет состоит из следующих этапов.

1. Сравнивается каждый уровень ряда со всеми предыдущими при этом

если то;;

при то;.

2. Вычисляются значения величин и:

;,

(10.20)

где	;
	.

Анализируя формулу (10.20), нетрудно заметить, что величина может принимать значения, причем, когда все уровни ряда равны между собой, и, когда ряд динамики монотонно убывает или возрастает. Показательхарактеризует тенденцию изменения дисперсии ряда динамики.

Показатель имеет нижний предел, равный , и верхний составляет. В первом случае ряд является монотонно убывающим, во втором - монотонно возрастающим. Кроме того, показатель может быть равен нулю:

---

• если все уровни ряда равны между собой, тогда 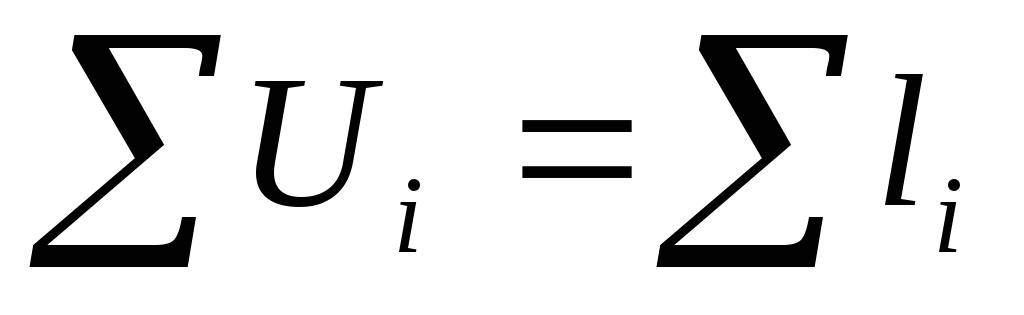. (Данное условие выполняется для ряда, который в первой половине является монотонно убывающим, а во второй - монотонно возрастающим.);

• если уровни подъема и спада чередуются, причем каждое следующее значение уровня подъема (спада) больше (меньше) всех последующих.

Перечисленные случаи, при которых показатель , представляют лишь теоретический интерес, и вероятность их использования при проведении практических расчетов крайне незначительна. Показатель характеризует изменение тенденций в среднем.

Оба показателя, и , асимптотически нормальны и имеют независимые распределения.

3. Проверяется с использованием 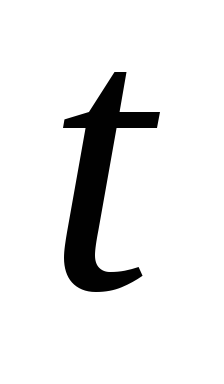-критерия Стьюдента гипотеза о том, можно ли считать случайными разност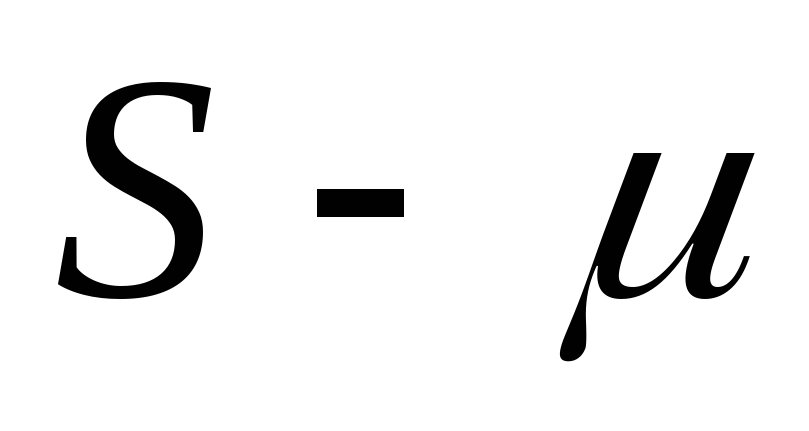ии: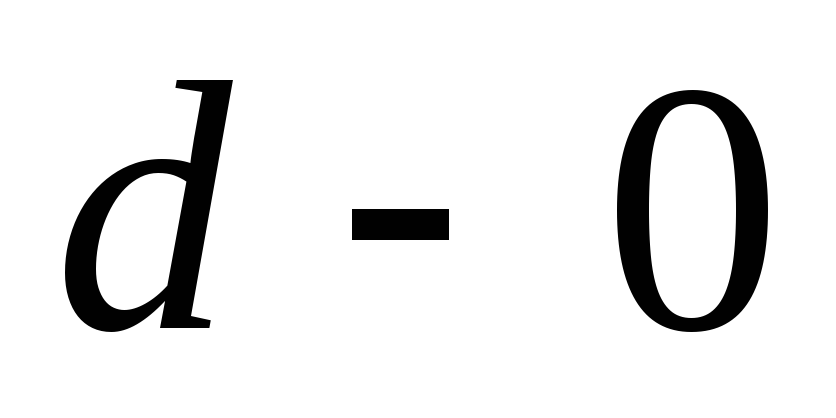

;,

(10.21)

где		среднее значение величины , определенное для ряда, в котором уровни расположены случайным образом;
		стандартная ошибка величины ;
		стандартная ошибка величины ;

---

Значения величин ,, итабулированы и приведены в приложении 13.

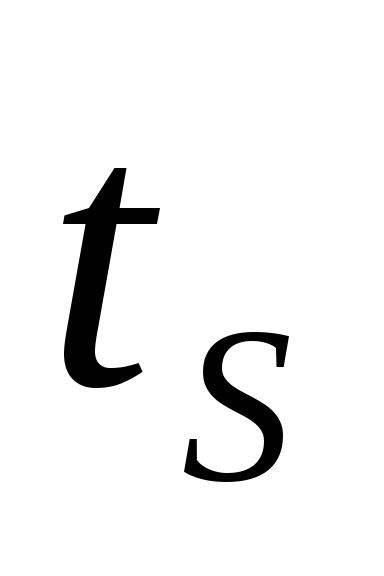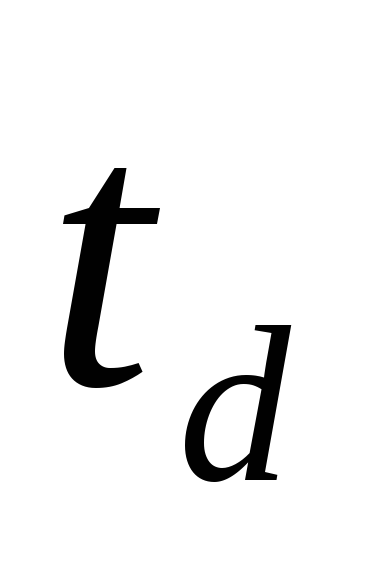4. Сравниваются расчетные значения и с табличным при заданном уровне значимости. Есл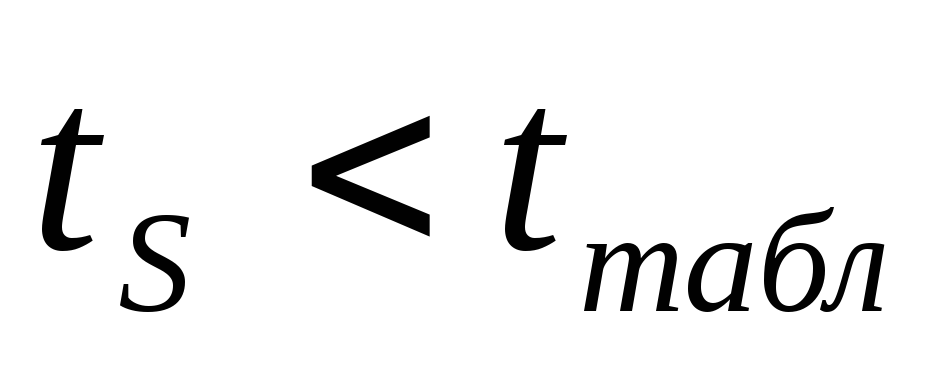ии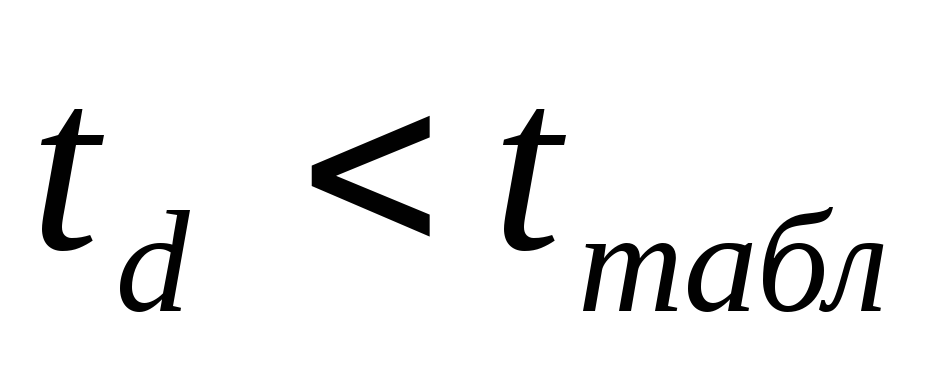, то гипотеза об отсутствии тренда в средней и дисперсии подтверждается.

---

10.6 Методы анализа основной тенденции (тренда) в рядах динамики

После того как установлено наличие тенденции в ряду динамики, производится ее описание с помощью методов сглаживания. Методы сглаживания разделяются на две основные группы:

• сглаживание или механическое выравнивание отдельных членов ряда динамики с использованием фактических значений соседних уровней;

• выравнивание с применением кривой, проведенной между конкретными уровнями таким образом, чтобы она отображала тенденцию, присущую ряду, и одновременно освободила его от незначительных колебаний.

Рассмотрим каждый из них.

Метод усреднения по левой и правой половине.Разделяют ряд динамики на две части, находят для каждой из них среднее арифметическое значение и проводят через полученные точки линию тренда на графике.

Метод укрупнения интервалов.Если рассматривать уровни экономических показателей за короткие промежутки времени, то в силу влияния различных факторов, действующих в разных направлениях, в рядах динамики наблюдается снижение и повышение этих уровней. Это мешает видеть основную тенденцию развития изучаемого явления. Поэтому для наглядного представления тренда применяется метод укрупнения интервалов, основанный на укрупнении периодов времени, к которым относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции и т.д.

Метод простой скользящей средней.Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем - средний уровень из такого же числа уровней начиная со второго, далее - начиная с третьего и т.д. Таким образом, при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень вначале и добавляя один следующий. Отсюда название -скользящая средняя.

Каждое звено скользящей средней - это средний уровень за соответствующий период, который относится к середине выбранного периода.

Для каждого конкретного ряда динамики () алгоритм расчета скользящей средней следующий.

1. Определить интервал сглаживания, т.е. число входящих в него уровней 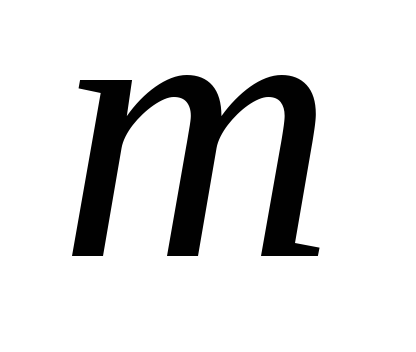(), используя правило: если необходимо сгладить мелкие, беспорядочные колебания, то интервал сглаживания берут по возможности большим, и, наоборот, интервал сглаживания уменьшают, когда нужно сохранить более мелкие волны и освободиться от периодически повторяющихся колебаний, возникающих, например, из-за автокорреляции уровней.

2. Вычислить среднее значение уровней, образующих интервал сглаживания, которое одновременно является сглаживающим значением уровня, находящегося в центре интервала сглаживания, при условии, что 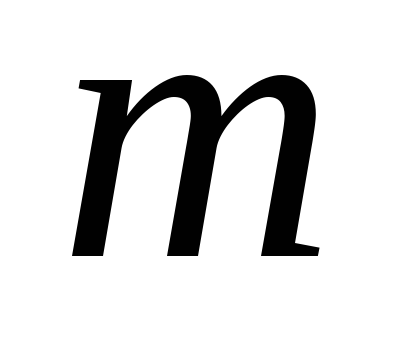- нечетное число, по одной из формул:

---
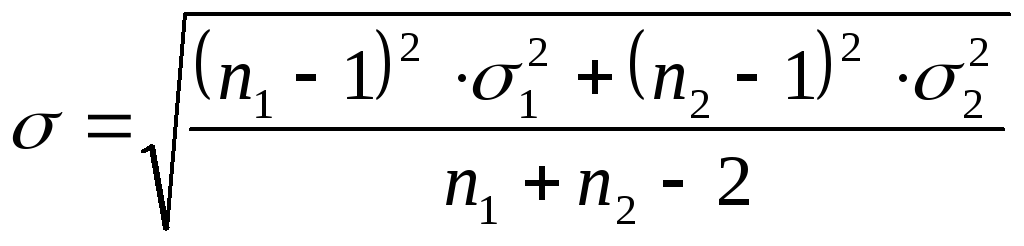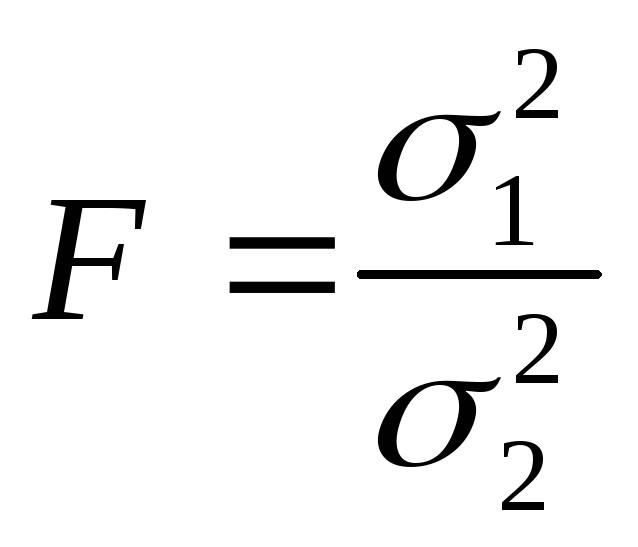