Файл: RT_dlya_bakalavrikov-2014.doc

Решение. Проведём аналитическое выравнивание показателей ряда динамики по уравнению параболы второго порядка, с применением способа отсчёта от условного начала.

.

Для расчёта параметров этого уравнения необходимо определить Для расчётов составляется таблица 31.

Параметры уравнения параболы второго порядка определяются по формулам:

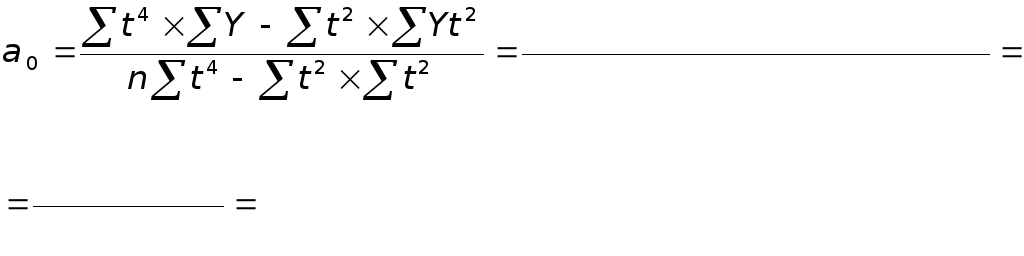
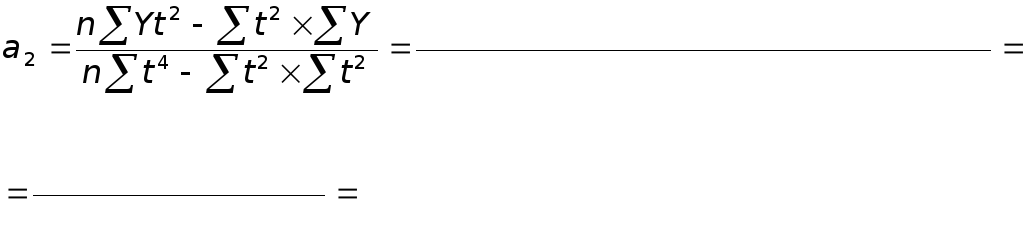
Таблица 31 – Аналитическое выравнивание численности безработных

в Курганской области по уравнению параболы

второго порядка

Таким образом, уравнение тренда примет следующий вид:

Подставляются в полученное уравнение значения t (из таблицы 31) и рассчитываются выровненные уровни численности безработных:

Изображаются фактические и выровненные уровни ряда динамики на графике:

–фактические уровни

–выровненные уровни

Рисунок 6 – Динамика численности безработных

в Курганской области

Вывод…..……………………………………………………………..…………….

…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….

Задание 53. По расчётам заданий 51 и 52 оцените степень приближения тренда к фактическим данным.

Решение. Рассчитывается среднее квадратическое отклонение, определённое по уравнениям прямой и параболы второго порядка.

Для расчётов составляется и заполняется таблица 32:

Таблица 32 – Данные для расчёта среднего квадратического отклонения

По уравнению прямой:

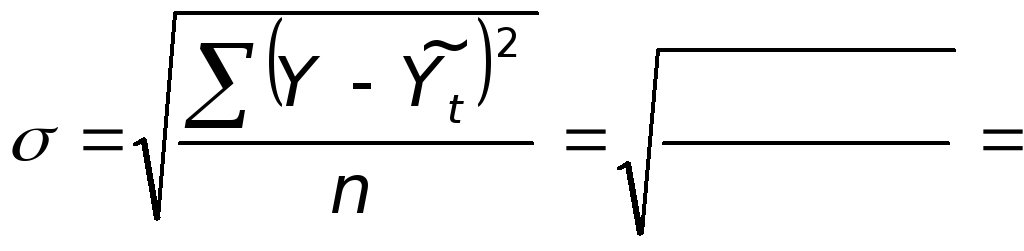
По уравнению параболы:

Вывод…..……………………………………………………………..…………….

…………………………………………………………………………………………….…

……………………………………………………………………………………………………………………………………………………………………………………………….

Задание 54. Имеются следующие данные о средней яйценоскости одной курицы-несушки по месяцам за три года, штук.

Определите показатели сезонных колебаний средней яйценоскости одной курицы-несушки по данным среднемесячного уровня за три года. Изобразите графически изменения сезонных колебаний. Сформулируйте выводы.

Решение. Определяется средние значения уровней ряда для каждого месяца года, общий средний уровень яйценоскости одной курицы-несушки и индексы сезонности по каждому месяцу. Расчёты проводятся в таблице 33.

Таблица 33 – Расчёт индексов сезонности средней яйценоскости

одной курицы-несушки

Общий уровень яйценоскости одной курицы-несушки в среднем по всей совокупности равен:

Изобразить полученные индексы сезонности в виде линейной диаграммы.

Рисунок 5 – Сезонные колебания яйценоскости кур-несушек

по месяцам

Вывод…..……………………………………………………………..…………….

…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….

Задание 55. По данным задания 48 рассчитайте эмпирические значения численности безработных в Курганской области с помощью линейной функции по уравнению прямой линии. Определите ожидаемую численность безработных на 2013 г., вероятностные границы, дайте интервальную оценку прогнозируемого явления. Сформулируйте выводы.

Решение. Составляется уравнение линейного тренда: .Для нахождения параметров этого уравнения необходимо решить систему уравнений:

{

Для решения системы уравнений необходимо определить Для расчётов составляется таблица 34 и решается система уравнений.

Таблица 38 – Динамика численности безработных в Курганской

области