ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.08.2024
Просмотров: 253
Скачиваний: 0
СОДЕРЖАНИЕ
4, 4, 2, 1, 4, 5 ,4, 3, 6, 5, 4, 4, 1, 2, 5, 4, 7, 3, 4, 2, 3, 1, 3, 2, 1, 2, 6.
Обобщающие статистические показатели
Статистическое изучение динамики
Статистическое изучение взаимосвязи социально-экономических явлений
Исходные данные для выполнения задания 15
Исходные данные для выполнения задания 21
Значения вероятностей, вычисленных для различных t (от 1 до 3)
Приложение 3 Величины коэффициента Стьюдента для различных значений доверительной вероятности
Приложение 4 Критические значения t-критерия Стьюдента для оценки значимости коэффициента корреляции
Вывод…..……………………………………………………………..…………….
…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….
Задание 24. Имеются данные о реализации магазином партии картофеля по дням недели.
|
Дни реализации |
Цена реализации за 1 кг, р. |
Общая выручка за 1 день, р. |
|
Пятница |
15,50 |
3565 |
|
Суббота |
15,80 |
10033 |
|
Воскресенье |
16,20 |
15876 |
|
Понедельник |
15,40 |
2849 |
|
Вторник |
15,30 |
3060 |
Определите среднюю цену реализации картофеля за 5 дней. Сформулируйте выводы.
Решение. Для расчёта средней цены реализации картофеля воспользуемся формулой …
Расчёты проведём по данным таблицы 12.
![]()
Вывод…..……………………………………………………………..…………….
…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….
Таблица 12 – Исходные и расчётные данные для решения задачи
|
Дни реализации |
Цена реализации за 1 кг, р. |
Общая выручка за 1 день, р. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ИТОГО |
|
|
|
Задание 25. Имеются данные за шесть лет о числе родившихся детей в Курганской области.
|
Показатель |
2007 г. |
2008 г. |
2009 г. |
2010 г. |
2011 г. |
2012 г. |
|
Число родившихся (живыми), чел. |
11159 |
11842 |
11943 |
11816 |
11589 |
12389 |
Рассчитайте число родившихся в среднем за 5 лет. Сформулируйте выводы.
Решение.
Так
как данные определяются по состоянию
на конец каждого года, интервалы между
датами равные (год) и данных на одну дату
больше, чем требуется для анализа,
поэтому для расчёта среднего числа
родившихся детей воспользуемся формулой
средней хронологической.
![]()
![]()
![]()
Вывод…..……………………………………………………………..…………….
…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….
Задание 26. Имеются о численности населения Курганской области. Рассчитайте общую численность населения, численность городского и сельского населения в среднем за последние 10 лет. Сформулируйте выводы.
|
Показатель |
2002 г. |
2003 г. |
2004 г. |
2005 г. |
2006 г. |
2007 г. |
2008 г. |
2009 г. |
2010 г. |
2011 г. |
2012 г. |
|
Численность населения (на конец года) - всего, тыс. чел. |
1016,2 |
999,4 |
981,0 |
961,8 |
946,1 |
934,5 |
925,2 |
918,6 |
908,8 |
896,3 |
885,8 |
|
в том числе: городского |
572,8 |
569,8 |
565,4 |
561,8 |
557,7 |
553,8 |
550,8 |
549,9 |
547,8 |
541,1 |
537,7 |
|
сельского |
443,4 |
429,7 |
415,6 |
400,0 |
388,4 |
380,7 |
374,4 |
368,7 |
361,0 |
355,2 |
348,1 |
Решение. Для расчёта средней численности населения воспользуемся формулой …
Средняя численность всего населения:

Средняя численность городского населения:

Средняя численность сельского населения:

Вывод…..……………………………………………………………..…………….
…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….
Задание 27. Имеются следующие данные о распределении рабочих организации по уровню месячной заработной платы.
-
Месячная заработная плата, р.
Число рабочих, чел.
9400 – 9500
10
9500 – 9600
20
9600 – 9700
48
9700 – 9800
60
9800 – 9900
42
9900 – 10000
20
Рассчитайте среднемесячную заработную плату одного рабочего, предварительно уменьшив до предела варианты (т. е. способом моментов). Сформулируйте выводы.
Решение. Рассчитывается среднемесячная заработная плата одного рабочего способом моментов по формуле:
![]() =
=
где
![]()
А =
Момент первого порядка определяется по формуле:
![]()
![]()
Для расчётов необходимо составить и заполнить таблицу 13.
Таблица 13 – Исходные и расчётные данные для решения задачи
|
Месячная заработная плата, р. |
|
|
|
Число рабочих, чел. |
|
|
9400 – 9500 |
|
|
|
10 |
|
|
9500 – 9600 |
|
|
|
20 |
|
|
9600 – 9700 |
|
|
|
48 |
|
|
9700 – 9800 |
|
|
|
60 |
|
|
9800 – 9900 |
|
|
|
42 |
|
|
9900 – 10000 |
|
|
|
20 |
|
|
ИТОГО |
|
|
|
|
|
Вывод…..……………………………………………………………..…………….
…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….
Задание 28. Распределение рабочих по уровню выполнения нормы выработки оказалось следующим.
|
Уровень выполнения нормы выработки, % |
Число рабочих, чел. |
|
До 99,9 |
21 |
|
100,0 – 104,9 |
59 |
|
105,0 – 109,9 |
112 |
|
110,0 – 114,9 |
48 |
|
115,0 и более |
10 |
Рассчитайте структурные средние процента выполнения нормы выработки рабочими цеха. Сформулируйте выводы.
Решение. Для расчёта моды используется формула:
![]()
Для определения медианы процента выполнения нормы выработки рабочими цеха необходимо заполнить таблицу 14.
Таблица 14 – Исходные и расчётные данные для решения задачи
|
Уровень выполнения нормы выработки, % |
Число рабочих, чел. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ИТОГО |
|
|
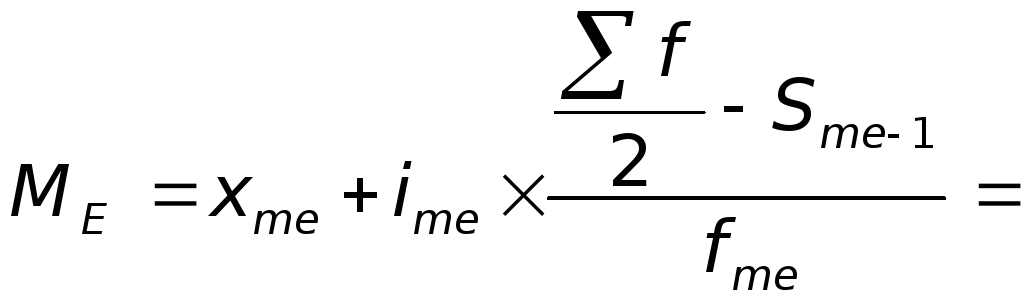
Вывод…..……………………………………………………………..…………….
…………………………………………………………………………………………….……………………………………………………………………………………………….………………………………………………………………………………………………….
Задание 29. Рассчитайте моду и медиану по данным о возрасте рабочих цеха.