Файл: Теория надёжности пустая рассчётка.doc

1.6. Определение коэффициента вариации

Коэффициент вариации представляет собой относительную безразмерную величину, характеризующая рассеивание показателя надежности. Коэффициент вариации

,(7)

где C – сдвиг(смещение) начала рассеивания показателя надежности.

При N>25, C= (8)

C=(мото-ч)

V=

1.7. Выбор теоретического закона распределения для выравнивания опытной информации

Для выравнивания распределения показателей надежности сельскохозяйственной техники и ее элементов наиболее широко используется закон нормального распределения (ЗНР) И закон распределения Вейбулла (ЗРВ).

В первом приближении теоретический закон распределения выбирают по коэффициенту вариации. При V<0,30, выбирают ЗНР, при V>0,50 – ЗРВ. Если значение коэффициента вариации находится в интервале 0,30….0,50 , то выбирают тот закон распределения, который лучше совпадает с распределением опытной информации. В нашем примере V=0,497, поэтому предварительнопринимаем оба закона.

1.7.1. Использование для выравнивания распределения опытной информации закона нормального распределения

Закон нормального распределения характеризуется дифференциальной (функцией плотностей вероятностей) и интегральной (функцией распределения) функциями. Отличительная особенность дифференциальной функции - симметричное рассеивание частных показателей надежности относительно среднего значения.

Дифференциальная функция описывается уравнением

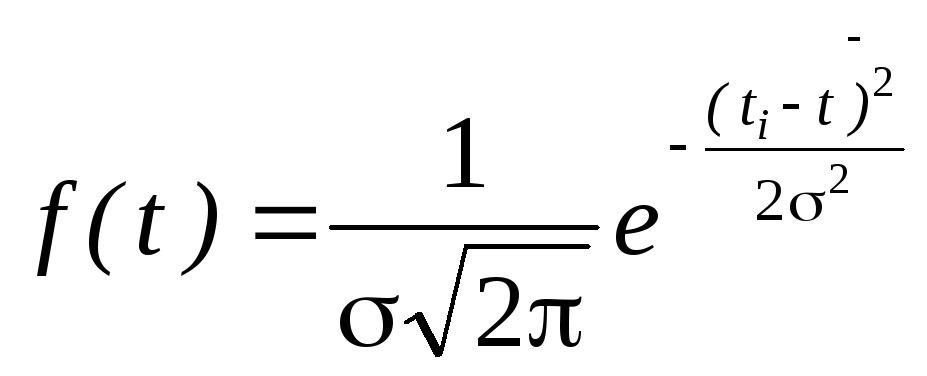(9)

Если t_i =0 и , то получим уравнение для центрированной, нормированной дифференциальной функции.

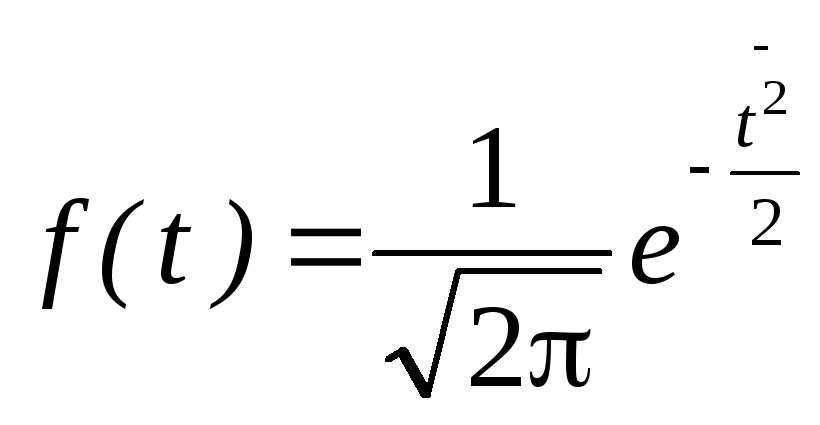
(10)

Центрированная нормированная дифференциальная функция посчитана и приведена в приложении 2 [2]. Для определения дифференциальной функции через центрированную нормируемую дифференциальную функцию, используют уравнения

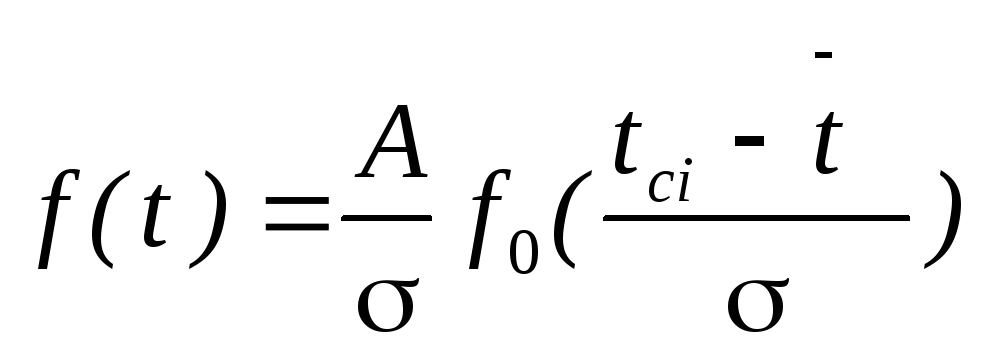, (11)

где А – длина интервала,

–среднее квадратичное отклонение,

t_ci – значение середины i-го интервала,

t – среднее значение показателя надежности.

Кроме того, следует пользоваться уравнением

(12)

Определим значения дифференциальной функции во всех интервалах статистического ряда

Интегральная функция (функция распределения)

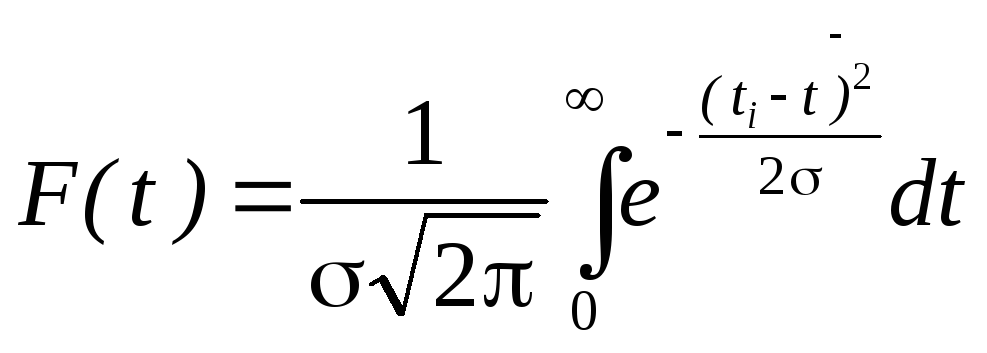
(13)

При t_i=0 и =1,00 ,то получим выражение для центрированной нормированной интегральной функции.

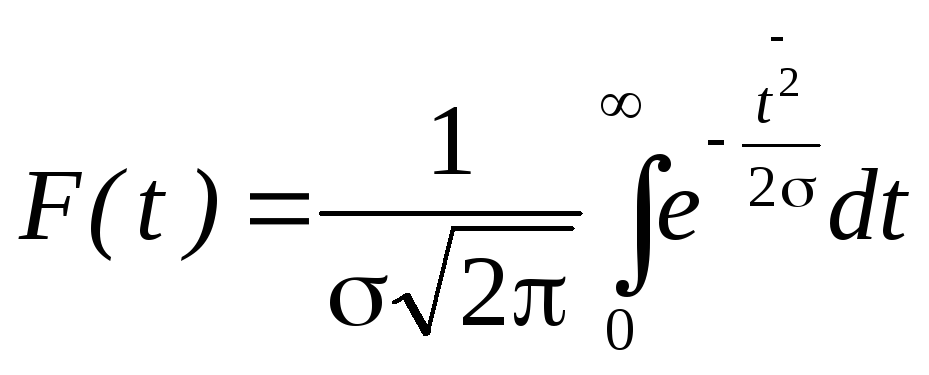(14)

Центрированная нормированная интегральная функция приведена в приложении 4 [2]. Для определения интегральной функции через

центрированную нормированную функцию, используют уравнение

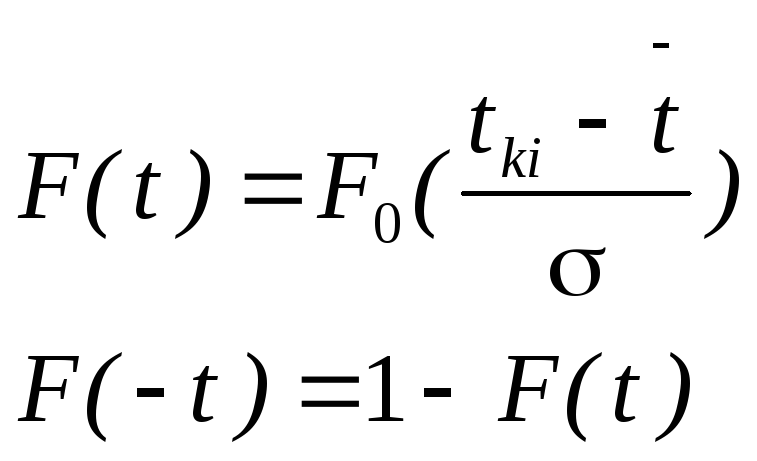(15)

Рассчитаем значения интегральной функции для всех интервалов статистического ряда

Рассчитанные значения функций сводим в таблицу

1.3. Значения дифференциальной и интегральной функций при знр

На основании полученных дифференциальных и интегральных функций могут быть построены интегральные и дифференциальные кривые.

Дифференциальная кривая заменяет полигон, интегральная кривая заменяет кривую накопленных опытных вероятностей

1.7.2. Использование для выравнивания распределения опытной информации закона распределения Вейбулла

Дифференциальную функцию или функцию плотностей вероятностей определяют по ЗРВ по уравнению

, (16)

где a,b – параметры ЗРВ.

Параметр b определяют по таблице. Из таблицы 3 выписывают параметр b коэффициенты k_b и c_{b ,} предварительно посчитав коэффициент вариации.

При V=

k_b= ;

b= ;

c_b= .

Параметр a рассчитывают по одному из уравнений

или , (17)

Отсюда получаем

(мото-ч)

Дифференциальную функцию при ЗРВ определяют по таблице 5 [3], используя уравнение

(18)

Рассчитаем значения функции во всех интервалах статистического ряда

Интегральную функцию или функцию ЗРВ определяют по уравнению

(19)

Интегральная функция приведена в таблице 6 [3]. При этом используют уравнение

(20)

Определяем значения интегральной функции во всех интервалах статистического ряда

Рассчитанные значения функций сводим в таблицу

1.4. Значения дифференциальной и интегральной функций при зрв