ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2024
Просмотров: 62
Скачиваний: 0
СОДЕРЖАНИЕ
1. Методика обработки полной информации
1.1.Составление сводной таблицы информации в порядке возрастания показателя надежности
1.1.Сводная таблица информации о доремонтных ресурсах двигателя
1.2. Составление статистического ряда
1.3. Определение среднего значения показателя надежности и среднего квадратичного отклонения
1.4. Проверка информации на выпадающие точки
1.5. Выполнение графического построения по данным статистического ряда
1.6. Определение коэффициента вариации
1.7. Выбор теоретического закона распределения для выравнивания опытной информации
1.3. Значения дифференциальной и интегральной функций при знр
1.7.2. Использование для выравнивания распределения опытной информации закона распределения Вейбулла
1.4. Значения дифференциальной и интегральной функций при зрв
1.5. Укрупненный статистический ряд
1.9.1. Определение доверительных границ рассеивания при законе нормального распределения
1.9.2. Определение доверительных границ рассеивания при законе распределения Вейбулла
1. Методика обработки полной информации
Рассмотрим методику обработки полной информации по показателям надежности на примере доремонтного ресурса двигателя типа СМД.
1.1.Составление сводной таблицы информации в порядке возрастания показателя надежности
1.1.Сводная таблица информации о доремонтных ресурсах двигателя
|
Номер двиг. |
Дорем. ресурс |
Номер двиг. |
Дорем. ресурс |
Номер двиг. |
Дорем. ресурс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.2. Составление статистического ряда
Статистический ряд исходной информации для упрощения дальнейших расчетов составляют в том случае, когда повторность информации N>25.При N<25 статистический ряд не составляют.
В нашем примере повторность информации N= >25,поэтому целесообразно составить статистический ряд, при этом информация разбивается на n-равных промежутков (интервалов), каждый из последующих должен прилегать к предыдущему без разрыва.
Число интервалов статистического ряда:
![]() +1,
(1)
+1,
(1)
где N – количество информации; n = = интервалов
Длина интервала:
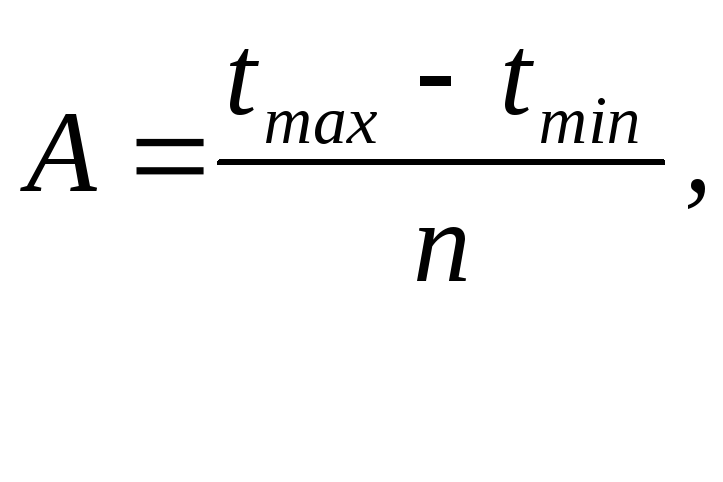 (2)
(2)
где tmax, tmin-наибольшее и наименьшее значение показателя надежности в сводной таблице информации. В нашем случае
(мото-ч)
1.2. Статистический ряд
|
Интервал, тыс. мото-ч. |
|
|
|
|
|
|
|
Опытная частота,mi |
|
|
|
|
|
|
|
Опытная вероятность,Pi |
|
|
|
|
|
|
|
Накопленная опытная вероятность
|
|
|
|
|
|
|
В первой строке указывают границы интервалов в единицах показателя надежности; во второй- число случаев (опытную частоту mi),попадающих в каждый интервал. Если точка информации попадает на границу интервалов, то в предыдущий и последующий
интервалы вносят
по 0,5 точки; в третьей строке –опытную
вероятность pi;
в четвертой- накопленную опытную
вероятность
![]() .
.
1.3. Определение среднего значения показателя надежности и среднего квадратичного отклонения
При наличии статистического ряда(при N>25),среднее значение показателя надежности
![]() ,(3)
,(3)
где n-число интервалов в статистическом ряду,
tci - значение середины i-го интервала,
Pi - опытная вероятность i-го интервала.
![]() =
=
(тыс. мото-ч)
Среднее квадратичное отклонение при наличии статистического ряда определяется по формуле:
![]() , (4)
, (4)
![]() =
=
0,461(Тыс. Мото-ч)
1.4. Проверка информации на выпадающие точки
Грубую проверку
на выпадающие точки проводят по правилу
3![]() :
:
![]() (5)
Нижняя граница:
(мото - ч)
(5)
Нижняя граница:
(мото - ч)
Верхняя граница: (мото - ч)
Наименьший доремонтный ресурс двигателя tдр.1= мото-ч, следовательно, эта точка информации действительна и должна быть учтена при дальнейших расчетах.
Наибольший ресурс двигателя tдр.28= мото-ч. Эта точка информации тоже действительна и должна быть учтена при дальнейших расчетах.
Более точно
информация на выпадающие точки проверяют
по критерию Ирвина
![]() ,теоретическое
значение которого
,теоретическое
значение которого![]() приведено в приложении 1[2].
приведено в приложении 1[2].
Фактическое значение критерия :
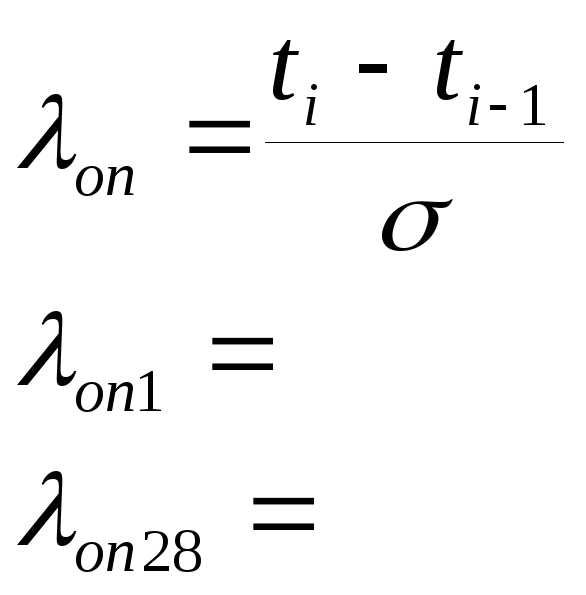 (6)
(6)
По приложению
1[2] находим, что при повторности информации
N=
и
![]() =
,
=
,![]() .
Первую точку информации следует
признать действительной, т.к <
.
Первую точку информации следует
признать действительной, т.к <![]() .
Последнюю точку информации следует
также признать действительной, т.к
<
.
Последнюю точку информации следует
также признать действительной, т.к
<![]()
1.5. Выполнение графического построения по данным статистического ряда
По данным статистического ряда могут быть построены гистограмма, полигон и кривая накопленных опытных вероятностей, которые дают наглядное представление об опытном распределении показателя надежности и позволяют решать ряд инженерных задач графическими способами.
Для построения гистограммы по оси абсцисс откладывают в определенном
масштабе показатель надежности t , а по оси ординат - опытную частоту mi или опытную вероятность Pi.
При построении полигона распределения по осям абсцисс и ординат откладывают те же значения, что и при построении гистограммы. Точки полигона распределения образуются пересечением ординаты, равной опытной вероятности интервала. Начальную и конечную точки полигона распределения приравнивают к абсциссам начала первого и конца последнего интервалов статистического ряда.
С помощью гистограммы и полигона распределения можно определить, например, число двигателей, которые достигнут предельного состояния и потребуют ремонта в заданном интервале наработки. Для этого определить площадь полигона или гистограммы, ограниченную заданным интервалом и отнести ее к суммарной площади под ступенчатым графиком гистограммы или под ломаной линией полигона. Полученное значение укажет на число отказавших двигателей в сотых долях единицы. Для получения числа физических двигателей необходимо это значение умножить на число точек информации.
Для построения
кривой накопленных опытных вероятностей
по оси абсцисс откладывают в масштабе
значение показателя надежности t,
а по оси ординат – накопленную опытную
вероятность
![]() .Точки
кривой накопленных опытных вероятностей
образуются пересечением ординаты,
равной сумме вероятностей
.Точки
кривой накопленных опытных вероятностей
образуются пересечением ординаты,
равной сумме вероятностей![]() ,
и абсциссы конца данного интервала.
Полученные точки соединяют прямыми
линиями. Первую точку соединяют с началом
первого интервала.
,
и абсциссы конца данного интервала.
Полученные точки соединяют прямыми
линиями. Первую точку соединяют с началом
первого интервала.
Кривая накопленных опытных вероятностей более удобна для решения практических задач по сравнению с гистограммой и полигоном распределения, т.к в этом случае нет необходимости определять площади, а все искомые показатели находят по оси ординат.