Добавлен: 21.10.2018
Просмотров: 1609
Скачиваний: 11
ЛЕКЦИИ 5-6
РАСЧЕТ ИЕРАРХИЧЕСКОЙ ДРЕВОВИДНОЙ КОНФИГУРАЦИИ СЕТИ.
4.1 Постановка задачи
Структура иерархически организованной информационной системы,
обеспечивающей сбор, обработку и вывод информации, может быть
представлена в виде дерева, корнем которого является, например,
информационно-вычислительный
центр,
промежуточными
вершинами
являются местные вычислительные центры, висячими вершинами - абоненты
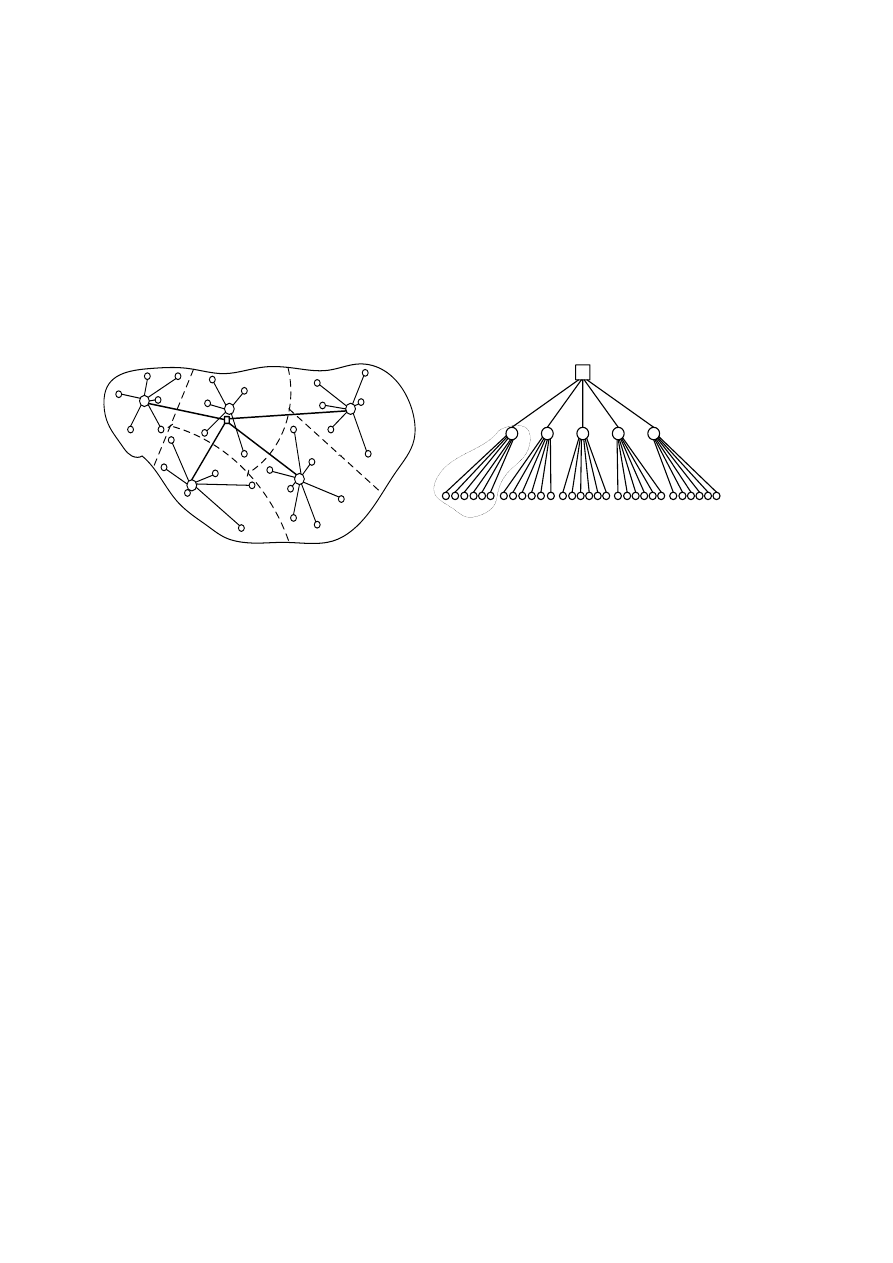
подразделения (рис.4.1 ).
а)
1
Г
2
Г
3
Г
4
Г
5
Г
1
Г
3
L
2
L
1
L
б)
Рис.4.1. Топологическая (а) и функциональная (б) организация связей
иерархической структуры.
Принимаем условие, что вновь создаваемые информационные центры
территориально размещаются при одном из существующих абонентов
подразделений, тогда рассчитываемая сеть представляет собой граф,
обеспечивающий покрытие всех узлов-абонентов.
Поставленная задача может быть сформулирована следующим образом:
заданы множество исходных узлов ????
????
∈ A мощностью N (i= 1, ????
̅̅̅̅̅̅) и взвешенные
расстояния ????
????????
между каждой парой узлов ????
????
,
????
????
. Каждый узел ????
????
характеризуется собственной оценкой ????
????
, трактуемой как количество
информации, передаваемое узлом за единицу времени. Требуется построить
сеть S минимальной длины, обеспечивающую многоуровневое покрытие
исходных узлов множества А и называемую иерархическим деревом.
Покрытие уровня h есть совокупность непересекающихся групп
{Г
р
}
ℎ
мощностью {????
Г
}
ℎ
. Каждая из групп Г
р
имеет единый центр Ц
????ℎ
,
размещающийся при одном из узлов ????
????
группы и соединяющийся с узлами,
принадлежащими группе, при этом заданное множество исходных узлов и
центров при них составляет нижний уровень покрытия h = 1.

Математическая
формулировка
задачи
отыскания
кратчайшей
иерархической древовидной сети предусматривает (в качестве критерия
эффективности) использовать ????
????????
-расстояния, взвешенные, например, одним из
соотношений (2.4) - (2.6).
Для получения строгой записи целевой функции необходимо определить
искомые неизвестные. Структура S будет считаться известной, если будет
установлено: 1) при каких исходных узлах множества А располагаются центры
групп каждого уровня; 2) с каким центром Ц
????ℎ
h-го уровня связан каждый узел
????
????
h-го уровня; 3) сколько уровней иерархии имеет структура S.
В качестве неизвестных первой группы будем рассматривать булевы
переменные, которые определяют местоположение центров Ц
????
:
????
????????
= {
1, если Ц
????
∈ ????
????
0, если Ц
????
∉ ????
????
} (4.1)
Набор матриц {‖????
????????
‖}
ℎ
для всех уровней структуры полностью определяет
местоположение всех центров Ц
????
, располагаемых на уровнях h.
В качестве неизвестных второй группы принимаем также булевы
переменные, которые определяют, с каким центром Ц
????ℎ
группы Г
????ℎ
связан
исходный узел ????
????
:
????
????????
= {
1, если ????
????
∈ Г
????ℎ
0, если ????
????
∉ Г
????ℎ
} (4.2)
Набор матриц {‖????
????????
‖}
ℎ
для всех уровней h структуры S полностью
определяет состав элементов в каждой группе Г
????ℎ
.
Неизвестное число уровней иерархии обозначим H, промежуточные уровни
структуры обозначим h, т.е. ℎ = 1, ????
̅̅̅̅̅. Кроме того, для записи математической
модели введем следующие обозначения:
М = ‖????
????????
‖, ????, ???? = 1, ????
̅̅̅̅̅– исходная матрица взвешенных расстояний между
каждой парой узлов ????
????
,
????
????
; {
????
????
} – оценка каждого узла структуры, которые
могут трактоваться как объем информации, поступающий в узел за единицу
времени;
Г
????ℎ
, p =
1, ????
Г
̅̅̅̅̅̅ – сформированная p-я группа, центры которых {Ц
????ℎ
}
составляют уровень h структуры S;

Ц
????ℎ
, p =
1, ????
Г
̅̅̅̅̅̅ - центральный узел Г
????ℎ
уровня h ;
П
ℎ
- оценочные коэффициенты Ц
????ℎ
, которые могут трактоваться как
способность узла обрабатывать объем информации, равный П
ℎ
в единицу
времени.
В сформулированной таким образом задаче наилучшей считается та
структура S, у которой величина суммарных взвешенных длин является
наименьшей. Таким образом, целевая функция модели может быть записана в
следующем виде:
???? = min
????,????,ℎ
∑
∑
∑
∑
(????
????????
)
ℎ
????
????=1
(????
????????
)
ℎ
(????
????????
)
ℎ
????
????=1
Г
????ℎ∈ℎ
????
ℎ=1
(4.3)
В (4.3) часть функционала ∑ ∑ (????
????????
)
ℎ
(????
????????
)
ℎ
(????
????????
)
ℎ
????
????
позволяет вычислить
суммарную длину взвешенных связей для одной группы Г
????ℎ
уровня h.
Переменная ????
????????
Выделяет из М столбец {
????
????
}, для которого Ц
????
∈ ????
????
.
Переменные ????
????????
выделяют из столбца {
????
????
}, те элементы, которые
соответствуют узлам, входящим в группу Г
????ℎ
.
Иерархическая древовидная структура требует выполнения следующих
функциональных ограничений, определяющих конфигурацию.
Каждый центр Ц
????
может располагаться только при одном узле ????
????
т.е.
∑
(????
????????
)
ℎ
????
????=1
= 1
(4.4)
Каждый узел ????
????
может входить только в одну группу уровня h , т.е.
∑
(????
????????
)
ℎ
????
????=1
= 1
(4.5)
Центры групп уровня h рассматриваются как совокупность исходных узлов
для уровня (h+1), т. е.
{Ц
р
}
ℎ
=
????
ℎ+1
(4.6)
Ограничения
на
пропускную
способность
узлов,
выражающие
необходимость согласования оценочных характеристик исходных узлов {????
????
} и
центров Ц
????
записывают в следующем виде:
0 ≤ П
????ℎ
− ∑
????
????????ℎ
????
????=1
????
????ℎ
< ????????????{????
????ℎ
} (4.7)
где ∞ >П
????ℎ
>0;
????
????
∈ Г
????ℎ
;
????
????
∉ Г
????ℎ

Физический смысл ограничения (4.7) состоит в том, что производи-
тельность П
????ℎ
центра Ц
????ℎ
должна быть не меньше, чем суммарные объемы
????
????ℎ
узлов
????
????
,
обслуживаемых
центром.
Однако,
недогруженность
производительности П
????ℎ
центра Ц
????ℎ
не должна превышать наименьшей
потребности узла ????
????ℎ
, не обслуживаемого центром Ц
????ℎ
.
Соотношения (4.1) - (4.7) представляют собой математическую постановку
задачи определения иерархической древовидной структуры, решение которой
позволит определить структуру S, отвечающую заданным требованиям.
Сформулированная задача принадлежит к классу нелинейных задач с
булевыми переменными.
Реальные объекты, для которых требуется определять структуры, имеют
размерности узлов N = 100 - 400. Мощность ????
ℎ
множества состояний уровня h
можно определить как число сочетаний из N по В элементов в группе, при этом
центры групп могут размешаться при каждом из N узлов, т.е.
????
ℎ
≈ ????! [(???? − 1)! (???? − ????)!]
⁄
для N=100 и В=10 ????
ℎ
= 5,2 *
10
15
4.2 Алгоритм расчета иерархической древовидной ВС
Из изложенного видно, что общий алгоритм решения рассматриваемой
нелинейной целочисленной задачи должен исключать необходимость явного
перебора всех допустимых вариантов.
Требуются методы, обеспечивающие частичный перебор ограниченного
числа допустимых вариантов и неявный перебор всех остальных вариантов, из
которых формируются допустимые варианты,
В целях сокращения множества вариантов объединения в группы
используется эвристический алгоритм, сущность которого заключается в том,
что для исходного уровня h = 1 на каждом шаге из не сгруппированных ранее
элементов определяется группа Г
????ℎ
, имеющая минимальную суммарную длину
взвешенных расстоянии и отвечающая ограничениям на конфигурацию и
пропускные способности узлов. С одной стороны, алгоритм позволяет снизить
размерность задачи, так как это дает возможность использовать понятие
упорядоченного перебора при формировании группы, но, с другой стороны,
поиск глобального оптимума заменяется поиском суммы локальных

оптимумов, т.е. вместо сформулированной в (3.8) целевой функции
эвристический алгоритм осуществляет поиск решения по целевой функции
вида:
???? = ∑
∑
min
????????
∑
∑
∑
(????
????????
)
ℎ
????
????=1
(????
????????
)
ℎ
(????
????????
)
ℎ
????
????=1
????
????=1
Г
????ℎ∈ℎ
????
ℎ=1
Изложенное обусловливает наличие в эвристическом алгоритме расчета
иерархической древовидной структуры двух этапов: целенаправленного
группирования и улучшения краевых точек.
На каждом шаге этапа целенаправленного группирования определяется
оптимальная группа Г
????ℎ
. Этап улучшения краевых точек обеспечивает
перераспределение сгруппированных элементов таким образом, чтобы, не
нарушая ограничений по конфигурации, получить более компактные группы.
Этот этап вступает в действие после определения второй и всех последующих
групп каждого уровня.
Для получения групп уровня h+1 производится корректировка оценочных
характеристик элементов на основании соотношения:
(????
????
)
ℎ+1
= ∑
????
????????
∑
????
????
????
????=1
????
????????
????
????=1
а также следует корректировать матрицу расстояний таким образом, чтобы в
матрицу М
ℎ+1
вошли только те столбцы и строки М
ℎ
, которые соответствуют
номерам узлов, при которых размещены центры групп.
Этап целенаправленного группирования. Этот этап ставит своей целью
определение группы с минимальной суммарной длиной связей между центром
группы и ее элементами. Группа считается найденной, если определены, при
каком элементе расположен центр группы, состав элементов, принадлежащих
группе, и число элементов, входящих в состав группы.
Этап целенаправленного группирования включает в свой состав следующие
вычислительные блоки (рис. 4.2): упорядочение (1) , определения группы (2) ,
вычеркивание (3) .