Добавлен: 21.10.2018
Просмотров: 1610
Скачиваний: 11
Аналогично п.1, формируем три матрицы: упорядоченную матрицу
)
2
(
M
;
матрицу номеров М
К(2)
, суммарную матрицу М
С(2)
.
3
5
9
3 5 9
3
5
9
3
0
0
0
3
3 5 9
3
0
0
0
5
50 50 70
5
5 3 5
5
50 50 70
9
100 70 100
9
9 9 3
9
150 120 170
Рис. 4.14 Матрица
)
2
(
M
Рис. 4.15 Матрица М
К(2
Рис. 4.16 Матрица М
С(2)
Минимальный элемент m
95
=120. Центр группы при 5-м узле, состав группы
Г
3
=5,3,9.
7) Улучшение группы Г
3
Центр улучшаемой группы Г
у
= Г
3
расположен при узле 5. Узлы 3,9 могут
корректироваться, если расстояние m
35
> m
32
либо m
95
> m
97
.По матрице
номеров М
К
, представленной на рис. 4.6, анализируем соответственно столбцы
3 и 9, которые приведены на рис. 4.17В 3-м столбце узел 2 находятся выше узла
5. Это означает, что центр Г
1
при узле 2 расположен к улучшаемому узлу 3
ближе, чем центр Г
3
, расположенный при узле 5. Поэтому корректировку узла 3
следует производить.
3 9
1 3 9
2 2 7
3 1 6
4 4 8
5 5 4
6 8 5
7 6 2
8 7 1
9 9 3
Рис. 4.17 Столбцы матрицы М
К
номеров

В 9-м столбце узел 7 находятся выше узла 5. Это означает, что центр Г
2
при
узле 7 расположен к улучшаемому узлу 9 ближе, чем центр Г
3
, расположенный
при узле 5. Поэтому корректировку узла 9 также следует производить.
В процессе корректировки узел 3 из группы Г
3
необходимо передать в группу
Г
1
(с центром в узле 2), а из группы Г
1
необходимо узел, ближайший к группе
Г
3
(с центром в узле 5), включить в состав группы Г
3
.
Группа Г
1
имеет для корректировки два узла –1 и 4. Чтобы найти, который из
этих узлов расположен ближе к центру 5 группы Г
3
, рассмотрим матрицу
номеров М
К
, представленную на рис. 5, точнее ее 5-й столбец, приведенный на
рис. 4.18. В этом столбце узел 4 расположен выше узла 2, следовательно,
необходимо узел 3 включить в состав Г
1
, а узел 4 – в состав Г
3
.
5
1 5
2 4
3 8
4 7
5 2
6 6
7 1
8 3
9 9
Рис. 4.18Столбец матрицы М
К
номеров
Кроме того, в процессе корректировки узел 9 из группы Г
3
необходимо
передать в группу Г
2
(с центром в узле 7), а из группы Г
2
необходимо узел,
ближайший к группе Г
3
(с центром в узле 5), включить в состав группы Г
3
.
Группа Г
2
имеет для корректировки два узла –6 и 8. Чтобы найти, который из
этих узлов расположен ближе к центру 5 группы Г
3
, рассмотрим 5-й столбец
матрицы номеров М
К
, приведенный на рис. 4.18. В этом столбце узел 8

расположен выше узла 7, следовательно, необходимо узел 8 включить в состав
Г
3
, а узел 4 – в состав Г
3
.
Таким образом, получаем скорректированные группы первого уровня:
Г
1
= 2,1,3; Г
2
= 7,6,9; Г
3
= 5,4,8.
8) В рассматриваемом примере вес каждого узла равен 1, а пропускные
способности центров групп П
h=1
=3. Для каждой из полученных групп
выполняется условие равенства пропускных способностей, поэтому
корректировка завершена.
Определение групп следующего уровня
9) Все узлы уровня h =1 сгруппированы, переходим к определению групп
уровня h = 2.
Исходными узлами для уровня h = 2 являются центры групп уровня h =1,
которые расположены при узлах 2,7,5.
10) Корректируем исходную матрицу М так, что в ней остаются
только центры групп (рис. 4.19)
М
(4)
2 5 7
2 0 35 50
5 35 0 30
7 50 30 0
Рис. 4.19 Скорректированная матрица М
(4)
11) Аналогично п.1 формируются три матрицы:
упорядоченная матрица М
(4)
(рис. 4.20); матрица М
(4)
номеров (рис. 4.21);
суммарная матрица М
(4)
(рис. 4.22).
2 5 7
2 5 7
2 5 7
2 0 0 0
2 2 5 7
2 0 0 0
5 35 30 30
5 5 7 5
5 35 30 30
7 50 35 50
7 7 2 2
7 85 65 80
Рис. 4.20Матрица
)
2
(
M
Рис. 4.21 Матрица
М
К(4)
Рис. 4.22 Матрица
М
С(4)
Минимальный элемент m
75
=65, тогда центр группы распложен при 5-м узле,
состав группы Г
1
=5,7,2.
Так как сформирована только одна группа, то процедура расчёта
заканчивается.
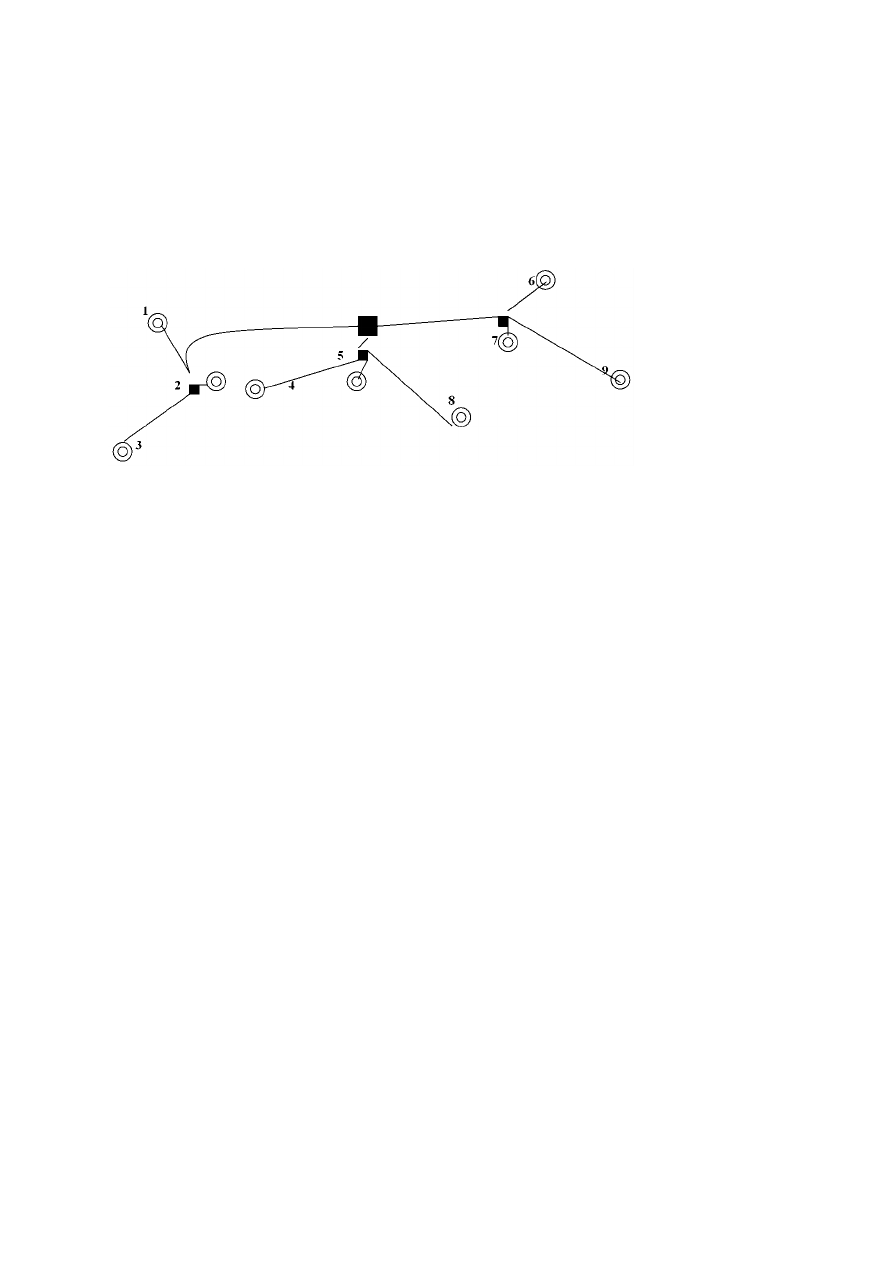
Результат расчета структуры представлен на рис. 4.23.
Рис. 4.23 Схема рассчитанной структуры.
Рассмотренный пример носит иллюстративный характер и предназначен для
пояснения процедуры расчета. Однако, как указывалось ранее, данная
процедура может быть использована для сетей, имеющих размерность 100—
400 исходных элементов.
Самоконтроль знаний
Контрольные вопросы
1. Какие примеры реальных ВС имеют иерархическую древовидную
конфигурацию (ИДК). Какие технические реализации соответствуют узлам и
дугам ИДК ?
2. Обоснуйте, что сформированные матрицы: ‖????‖
ℎ
, ‖
????‖
ℎ
полно и однозначно
описывают ИДК ВС.
3. Почему отсутствие одной из групп ограничений 4.4 – 4.7 может привести к
неправильному решению поставленной задачи?
4. Почему сформулированная математическая постановка задачи определения
ИДК относится к классу нелинейных задач с булевскими переменными?

5. Почему в предложном алгоритме определения ИДК необходим этап
корректировки матрицы?
6. Почему предложенная эвристическая процедура решения не гарантирует
глобального оптимума целевой функции.
Контрольные задания
1. Поясните, как выбраны номера в 4-м столбце матрицы M
K
, учитывая, что
в 4-м столбце матрицы
M
4-й и 5-й элементы имеют одинаковые значения.
2. Поясните, почему этап корректировки начинается только после
определения второй группы?
3. Как объяснить, почему при выполнении любого этапа корректировки
используется матрица M
K
, сформированная на первом этапе выполнения
расчетов.
4. Подтвердите расчетом возникновение ошибки по п. 5 примера, если вместо
матрицы М
К
, (рис. 4.6), использовать матрицу М
К(1)
(рис. 4.11)