Добавлен: 21.10.2018
Просмотров: 1615
Скачиваний: 11
Начало
Упорядочение
Вычеркивание
Определение
группы
Количество
групп>1?
Корректировка
М⁰ ,{Iᵢ}
В уровне
одна группа?
Конец
Все группы
уровня
Выполняется усло-
вие пропускной
способности уз-
ла?
Определение
заменяющего
элемента
Определение
наименее
удаленного
центра
Определение
близлежащей
группы
нет
да
да
нет
нет
да
нет
Э
та
п
ц
е
л
е
н
ап
р
ав
л
е
н
н
о
го
г
р
уп
п
и
р
о
ва
н
и
я
Э
та
п
у
л
уч
ш
е
н
и
я
кр
ае
вы
х
т
о
че
к
да
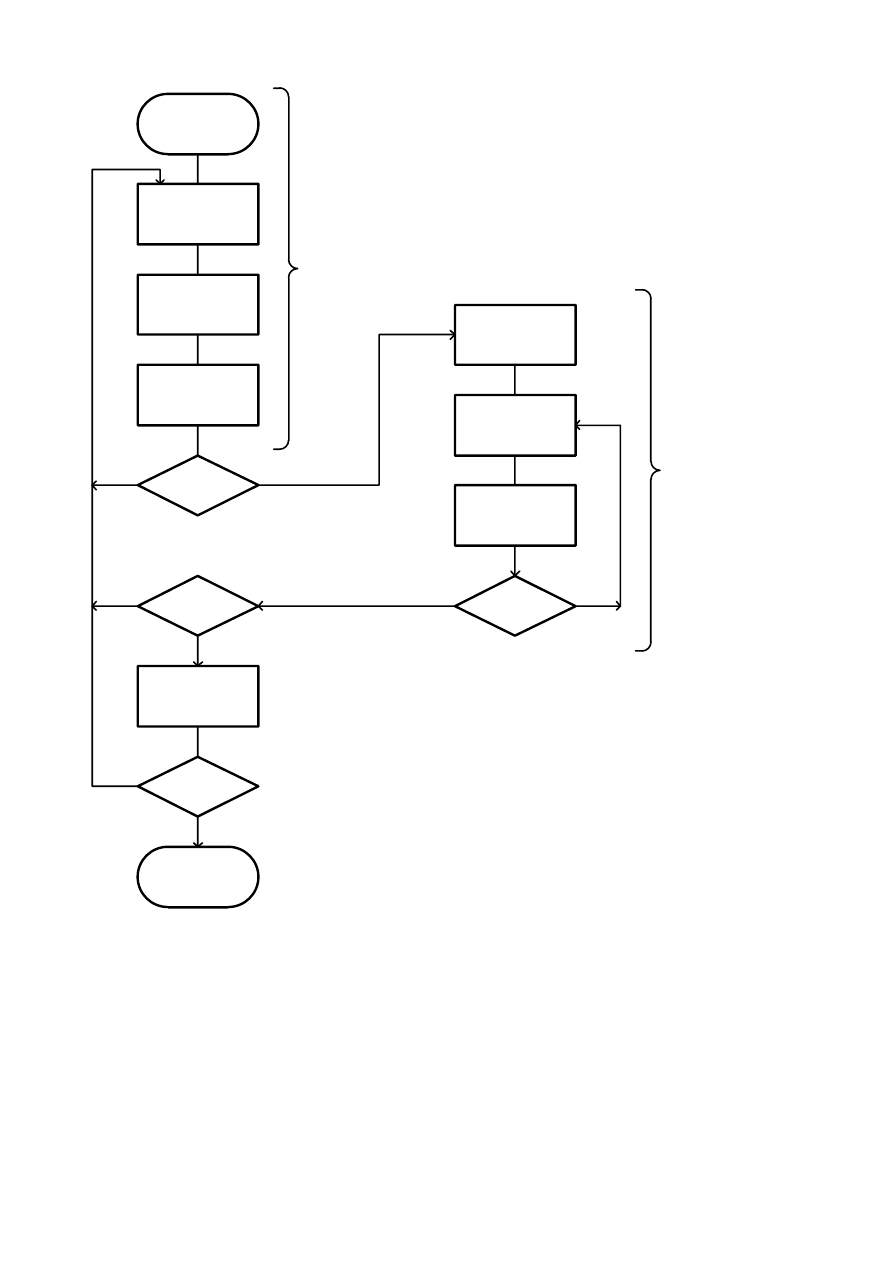
Рис. 4.2 Укрупненная блок-схема алгоритма определения иерархической
древовидной структуры
В результате вычислительных операций блока упорядочениями исходной
матрицы M получаем три матрицы: упорядоченную М
̅ = ‖????
????????
̅̅̅̅̅‖, номеров М
К
=
‖????
????????
????
‖ и суммарную М
С
=
‖????
????????
????
‖.
Для получения каждого j-го столбца упорядоченной матрицы необходимо
расположить по возрастанию значения всех элементов j-го столбца исходной

матрицы M, кроме диагонального. Диагональный элемент записывается первым
в упорядоченной матрице. Таким образом, при выполнении процедуры
упорядочения должны выполняться следующие соотношения:
∀???? = ????; ????
̅
1????
∈ {????}
????
, ????, ???? = 1, ????
̅̅̅̅̅
(4.8)
∀???? ≠ ????; ????
̅
????????
= min
i
[{m}
j
\ ⋃ m
ij
i
] , ???? = 2, ????
̅̅̅̅̅
(4.9)
где {????}
????
– j-й столбец матрицы М.
Одновременно с получением j-го столбца {????
̅}
????
упорядоченной матрицы М
̅
формируется j-й столбец {????
к
}
????
матрицы номеров М
к
, элементами которого
являются порядковые номера элементов j-го столбца {????}
????
исходной матрицы
М, записанные в соответствии с расположением элементов в столбце {????
̅ }
????
, т,е.
если ????
????????
=
????
????????
̅̅̅̅̅, то ????
????????
????
= b (4.10)
Каждый j-й столбец суммарной матрицы М
С
получается в результате
последовательного суммирования элементов столбца упорядоченной матрицы
М
̅ т.е.
????
????????
????
= ∑
????
̅
????????
????
????=1
(4.11)
где ????, ????, ???? = 1, ????
̅̅̅̅̅
В вычислительном блоке определения группы последовательно выполняются
следующие операции.
1. Просматривается i-я строка {
????
????
}
????
. суммарной матрицы ????
????
и
отыскивается минимальный элемент:
????
????????
????
= min
????
{????
????
}
????
.
2. Принимаем, что при элементе
????
????
располагается центр Ц
????
группы,
содержащей в своем составе i узлов.
3. По столбу с номером d матрицы номеров {
????
к
}
????
определяем номера
первых i (по числу просмотренных строк в М
c
) узлов, входящих в группу
с центром, разместившимся в ????
????
.
4. Присваиваем i значение
????
????????
= 1 (???? ∈ {????
к
}
????
) .
5. Проверяем для найденной группы, содержащей i узлов, ограничение (4.7).
Если ограничение (4.7)выполняется, то j увеличивается на единицу, и
переходим к п. 1. Если ограничение (4.7) не выполняется, то принимаем в
качестве решения состав группы, найденный на шаге i -1.
После того как состав группы определен (определены номера элементов,
входящих в группу) и определено местоположение центра группы (номер

столбца, который соответствует минимальному значению {????
????
}
????
,, переходим к
блоку вычеркивания, в котором всем элементам строк и столбцов исходной
матрицы М, номера которых соответствуют элементам, вошедшим в группу Г
р
присваивается значение ∞ .
Далее, в соответствии с алгоритмом (рис. 4.2) проверяют, какое число групп
уровня получено (оператор 4) . В том случае, если найдена вторая и
последующие группы, то переходят к этапу улучшения краевых точек.
Этап улучшения краевых точек. Этот этап ставит своей целью осуществить
последовательный обмен наиболее удаленных элементов улучшаемой группы с
элементами соседних групп, которые наименее удалены от центра улучшаемой
группы. Обеспечение компактности улучшаемой группы достигается
корректировкой в целях получения группы, имеющей односвязную область
определения.
Процедура эвристического этапа улучшения краевых точек начинается
после того, как найдено не менее двух групп, она включает в себя следующее:
1. Определение центров близлежаших групп {Ц
′
}
ℎ
(оператор 5). Центры
сгруппированных элементов уровня h принадлежат множеству, если расстояния
{????
Цу,Цр
} от центра Ц
у
улучшаемой группы Г
у
(которая определена последней)
до центров {Ц
????
} ранее определенных групп меньше расстояния от Ц
у
до
наиболее удаленного элемента ????
????
, принадлежащего улучшаемой группе Г
у
:
Ц
????
∈ {Ц
′
}
ℎ
, если
????
Цу,Цр
<
????
Цу,????????
(4.12)
2. Определение центра Ц
????
∗
, наименее удаленного от ????
????
(оператор 6). Элемент
множества {Ц
′
}
ℎ
принадлежит множеству
{Ц
′′
}
ℎ
, если расстояние ????
????Ц
′
меньше
расстояния ????
????Ц
у
:
Ц
????
∈ {Ц
′′
}
ℎ
, если ????
????Ц
′
<
????
????Ц
у
(4.13)
Наименее удаленный центр Ц
????
∗
соответствует такому элементу множества
{Ц
????
′′
}
ℎ
, у которого наименьшее значение ????
????Ц
′′
:
Ц
∗
= Ц
????
∗
, если ????
????????
=
min
{Ц
′′
}
????
????Ц
′′
(4.14)
3. Определение элемента ????
????
′
, заменяющего ????
????
(оператор 7). Элемент
????
????
,
принадлежащей группе с центром Ц
????
∗
может заменять
????
????
в улучшаемой группе

Г
у
, если расстояние ????
????Ц
у
, является наименьшим из всех элементов группы с
центром Ц
????
∗
, т.е.
????
????
≔ ????
????
, если ????
????
′
∈ Г
у
,
????
????
∈ Г
Ц
∗
;
????
????Ц
у
=
min
????
????∈ГЦ
∗
????
????Ц
у
(4.15)
4. Проверка групп Г
Цу
и Г
Ц
∗
на ограничение по производительности состоит
в проверке выполнения ограничения (4.7) на пропускную способность узлов
для обеих групп (оператор 5).
Если ограничение (4.7) выполняется, то состав групп Г
Цу
и Г
Ц
∗
корректируется путем взаимного обмена элементов ????
????
и
????
????
;
. Если ограничение
(4.7) не выполняется, делается попытка определить следующий элемент ????
????
;
. из
Г
Ц
∗
, используя пп. 3 и 4, затем проверяются все группы, принадлежащие
множеству {Ц"} .
Решение по второму этапу продолжается до тех пор, пока все группы,
принадлежащие множеству {Ц"} , не будут проверены.
После определения групп уровня h переходят к определению групп уровня
h+1 (оператор 9). В начале расчета корректируется исходная матрица М
ℎ
(оператор 10), в которой остаются столбцы и строки, соответствующие
найденным центрам групп уровня h, а также оценивается каждый центр группы
путем суммирования оценок элементов, входящих в соответствующую группу.
Процедура расчета завершается, если на уровне H формируется только одна
группа (оператор 11).
Изложенная методика использует принцип целенаправленного поиска,
обеспечивающий получение решения в точке локального оптимума целевой
функции, которое затем корректируется эвристической процедурой улучшения
краевых точек. Проведенные исследования [18] показали, что процедура
обеспечивает среднюю точность расчета 5%, что соизмеримо с точностью
исходных данных.
Пример 4.3
Даны узлы (N=9), заданы взвешенные расстояния, представленные в матрице
М на рис. 4.3.
М=
1
2
3
4
5
6
7
8
9
1
0
10 24 21 45 65 60 55 100
2
10 0
15 11 35 55 50 48 90
3
24 15 0
25 50 70 75 60 100
4
21 11 25 0
25 45 40 35 60
5
45 35 50 25 0
40 30 26 70
6
65 55 70 45 40 0
12 30 40
7
60 50 75 40 30 12 0
18 28
8
55 48 60 35 26 30 18 0
40
9
100 90 100 60 70 40 28 40 0
Рис. 4.3 Матрица М взвешенных расстояний
Требуется построить древовидную иерархическую сеть минимальной длины,
обеспечивающую многоуровневое покрытие исходных узлов. Например, так,
как показано на рис. 4.4.
Рис. 4.4. Древовидная иерархическая структура
Итак, исходные данные для расчета следующие: N=9; количество узлов, z
i
=1;
веса узлов, которые равны количеству информации, передаваемой узлом за
единицу времени
9
,
1
i
,
П
h=1
=3; пропускные способности центров групп h=1;
П
h=2
=9, пропускные способности центров групп h=2.