ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Электроника
Добавлен: 23.10.2018
Просмотров: 11039
Скачиваний: 27
81
( )
0
0
1 .
T
U
p
p
e
ϕ
⎛
⎞
Δ
=
−
⎜
⎟
⎝
⎠
(2.18а)
Вторую граничную концентрацию запишем в виде
( )
0
p w
Δ
= , (2.18б)
поскольку концентрации носителей на омическом контакте со-
храняют равновесное значение независимо от распределения
концентраций в базе. При выполнении граничных условий (2.18)
коэффициенты
1
A и
2
A имеют значения:
( )
1
0
,
2
w
L
p
A
e
w
sh
L
−
Δ
=
⎛ ⎞
⎜ ⎟
⎝ ⎠
( )
2
0
,
2
w
L
p
A
e
w
sh
L
Δ
=
⎛ ⎞
⎜ ⎟
⎝ ⎠
(2.19)
а
распределение
( )
p x
Δ
принимает
вид
:
( )
0
1
.
T
U
w
x
sh
L
p x
p
e
w
sh
L
ϕ
−
⎛
⎞
⎛
⎞ ⎜
⎟
⎝
⎠
⎜
⎟
Δ
=
−
⎛ ⎞
⎜
⎟
⎝
⎠
⎜ ⎟
⎝ ⎠
(2.20)
В
случае
толстой
базы
(
)
2 3
w
L
>
−
можно
положить
w
→ ∞
Тогда
коэффициенты
1
A
и
2
A
упрощаются
:
1
0
A
= ;
( )
2
0
A
p
= Δ
,
а
распределение
дырок
оказывается
экспоненциальным
( )
0
0
1
.
T
x
U
L
p
p
e
e
−
ϕ
⎛
⎞
Δ
=
−
⎜
⎟
⎝
⎠
(2.21
а
)
В
случае
тонкой
базы
0.5
w
L
<
можно
считать
shz
z
≈ .
То
-
гда
из
(2.20)
получаем
практически
линейное
распределение
примесей
в
базе
( )
0
1 1
,
T
U
x
p x
p
e
w
ϕ
⎛
⎞⎛
⎞
Δ
=
−
−
⎜
⎟⎜
⎟
⎝
⎠
⎝
⎠
(2.21
б
)
которое
более
характерно
для
реальных
диодов
.
На
рис
. 2.11, а
распределения
(2.21
а
)
и
(2.21
б
)
показаны
соответственно
сплош
-
ными
и
пунктирными
линиями
.
Для
режима
экстракции
(
)
0
U
<
все
выведенные
формулы
остаются
в
силе
,
а
соответствующие
распределения
дырок
и
электронов
показаны
на
рис
. 2.11, б.

82
Вольт-амперная характеристика.
Для
получения
вольт
-
амперной
характеристики
продифференцируем
выражение
(2.20)
по
координате
x
и
,
подставив
в
(1.20
а
),
получим
распределение
плотности
дырочного
тока
в
базе
( )
0
1
.
T
б
U
pб
б
pб
p
б
pб
pб
w
x
ch
qD
p
L
j
x
e
w
L
sh
L
ϕ
− −
⎛
⎞
=
−
⎜
⎟
⎝
⎠
(2.22
а
)
Здесь
для
определенности
введены
индексы
для
базового
слоя
и
для
«
рабочих
»
носителей
—
дырок
.
По
аналогии
можно
записать
для
плотности
электронного
тока
в
эмиттерном
слое
:
( )
0
1
,
T
э
U
nэ
э
nэ
n
э
pб
nэ
w
x
ch
qD n
L
j
x
e
w
L
sh
L
ϕ
− −
⎛
⎞
=
−
⎜
⎟
⎝
⎠
(2.22
б
)
где
nэ
L
—
диффузионная
длина
для
электронов
в
эмиттере
,
а
ко
-
ордината
х
отсчитывается
от
перехода
в
глубь
эмиттера
.
Полагая
0
x
=
в
формулах
(2.22),
умножая
обе
части
на
площадь
s
и
скла
-
дывая
токи
( )
0
p
I
и
( )
0
n
I
,
получаем
искомую
вольт
-
амперную
ха
-
рактеристику
идеализированного
диода
.
Необходимо
помнить
,
что
уменьшение
диффузионной
составляющей
плотности
тока
сопровождается
ростом
дрейфовой
составляющей
.
Обычно
ста
-
тическую
вольт
-
амперную
характеристику
записывают
в
сле
-
дующей
форме
:
0
1 ,
T
U
I
I
e
ϕ
⎛
⎞
=
−
⎜
⎟
⎝
⎠
(2.23)
где
0
0
.
pб
nэ
б
э
б
pб
pб
nэ
pб
qD s
qD s
I
p
w
w
L th
L th
L
L
=
+
⎛
⎞
⎛
⎞
⎜
⎟
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
(2.24)
83
I
1
2
3
4
3
2
1
0
-10
-40
U
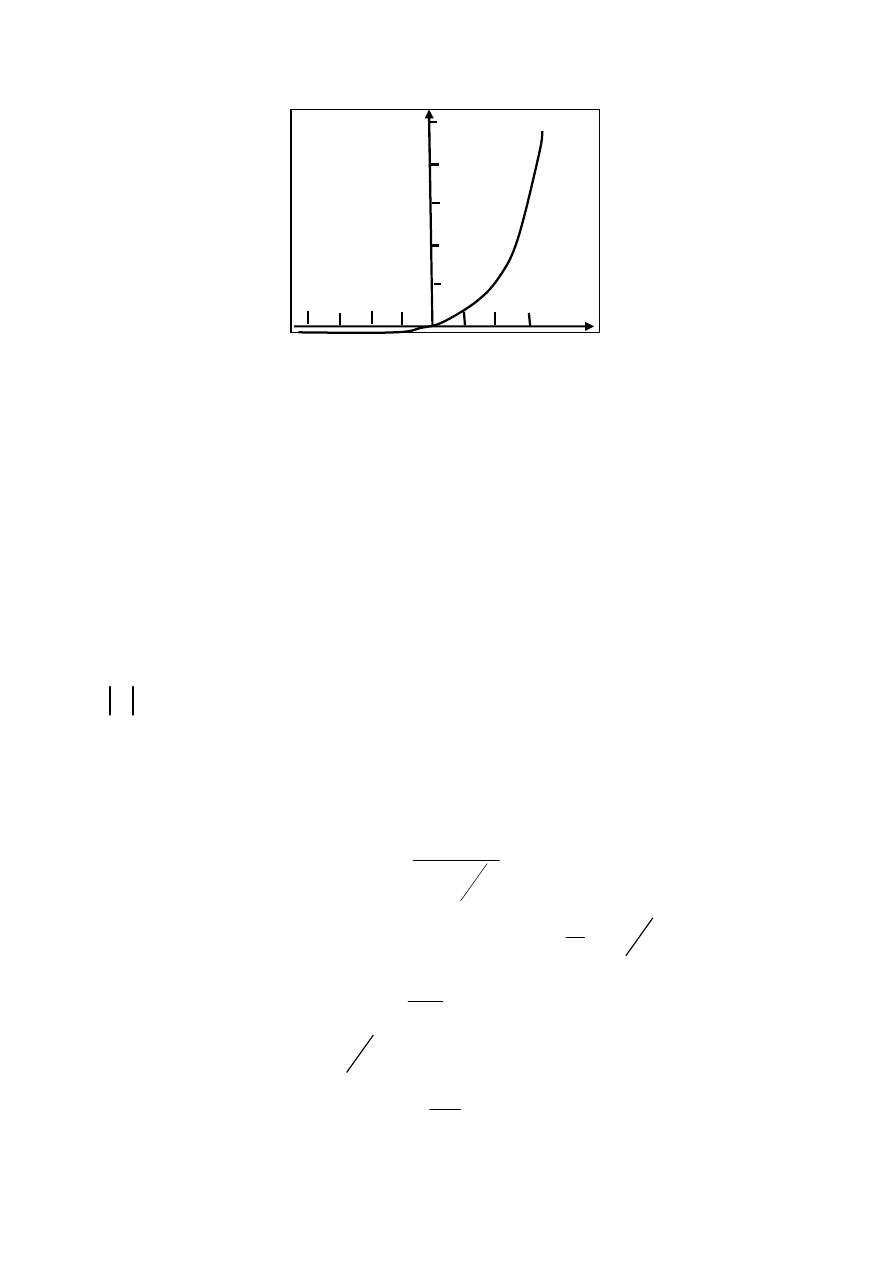
Рис. 2.12 — Статическая вольт-амперная характеристика
идеализированного плоскостного диода
Формула
(2.23) —
одна
из
важнейших
в
транзисторной
тех
-
нике
—
представлена
на
рис
. 2.12. Ток
0
I
, определяющий
«масштаб» характеристики, называется тепловым током.
Термин «тепловой» отражает сильную температурную зави-
симость тока
0
I
, а также тот факт, что он равен нулю при аб-
солютном нуле температуры. Другим распространенным тер-
мином является «обратный ток насыщения», происхождение
которого связано с тем, что при отрицательном напряжении
T
U
>> ϕ обратный ток идеализированного диода равен —
0
I
и
не зависит от напряжения.
Вторым
слагаемым
в
(2.24)
обычно
пренебрегают
,
т
.
к
.
ин
-
жекция
электронов
из
базы
в
эмиттер
очень
мала
.
Тогда
тепловой
ток
равен
0
0
.
(
)
б
DS
I
q
p
w
Lth
L
≈
(2.25
а
)
Если
выполняется
условие
w
L
<<
w
w
th
L
L
⎛ ⎞ ≈
⎜ ⎟
⎝ ⎠
,
0
0
.
DS
I
q
p
w
≈
(2.25
б
)
При
w
L
>>
( )
1
w
th
L
≈
0
0
.
Ds
I
q
p
L
≈
(2.26)

84
Свойства
теплового
тока
будут
подробно
рассмотрены
поз
-
же
.
Сейчас
только
заметим
,
что
тепловой
ток
диода
пропорцио
-
нален
концентрации
неосновных
носителей
электронного
полу
-
проводника
0б
p
,
которая
жестко
связана
с
собственной
концен
-
трацией
i
n
.
Собственная
концентрация
i
n
у
кремния
гораздо
меньше
,
чем
у
германия
,
следовательно
,
и
тепловой
ток
у
крем
-
ниевых
диодов
несравненно
меньше
,
чем
у
германиевых
.
Одной
из
важных
особенностей
характеристики
(2.23)
явля
-
ется
очень
крутая
(
экспоненциальная
)
прямая
ветвь
.
Поэтому
весьма
большие
прямые
токи
порядка
нескольких
ампер
и
выше
получаются
у
полупроводниковых
диодов
при
напряжении
не
более
1
В
,
т
.
е
.
намного
меньшем
,
чем
в
случае
вакуумных
и
газо
-
наполненных
диодов
.
В
связи
с
большой
крутизной
прямой
ветви
обычно
удобнее
задавать
в
качестве
аргумента
ток
,
а
напряжение
считать
его
функцией
,
т
.
к
.
задать
на
практике
напряжение
с
вы
-
сокой
точностью
бывает
трудно
.
Соответственно
,
формулу
(2.23)
целесообразно
преобразовать
к
следующему
виду
0
ln
1 .
T
I
U
I
⎛
⎞
= ϕ
+
⎜
⎟
⎝
⎠
(2.27)
Вентильные
свойства
любого
диода
выражены
тем
ярче
,
чем
меньше
обратный
ток
при
заданном
обратном
напряжении
и
чем
меньше
прямое
напряжение
при
заданном
прямом
токе
.
К
сожа
-
лению
,
эти
два
требования
в
данном
случае
противоречивы
.
В
самом
деле
,
из
формулы
(2.26)
видно
,
что
изменение
теплового
тока
,
какими
бы
причинами
оно
ни
вызывалось
,
сопровождается
изменением
прямого
напряжения
в
противоположном
направле
-
нии
.
Это
хорошо
видно
из
рис
. 2.13, а,
где
различие
токов
0
I
обу
-
словлено
разницей
в
площадях
переходов
при
прочих
равных
ус
-
ловиях
.
Важным
следствием
этой
общей
зависимости
является
то
,
что
прямые
напряжения
у
кремниевых
диодов
заметно
боль
-
ше
,
чем
у
германиевых
,
поскольку
тепловой
ток
у
первых
на
не
-
сколько
порядков
меньше
.
Различие
в
прямых
напряжениях
гер
-
маниевых
и
кремниевых
диодов
составляет
обычно
0,3–0,4 В
и
сохраняется
вплоть
до
малых
токов
.
Характеристические сопротивления.
Нелинейность
ха
-
рактеристики
удобно
оценивать
,
сопоставляя
сопротивления
дио
-
да
при
смещениях
в
прямом
и
обратном
направлениях
.
85
I
Ge
Si
6
5
4
3
2
1
мА
U
0 0,2 0,4 0,6 0,8
0 0,2 0,4 0,6 0,8
I
мА
2
1,5
1
0,5
-100
-50
s
1
s
2
>s
1
U
а
б
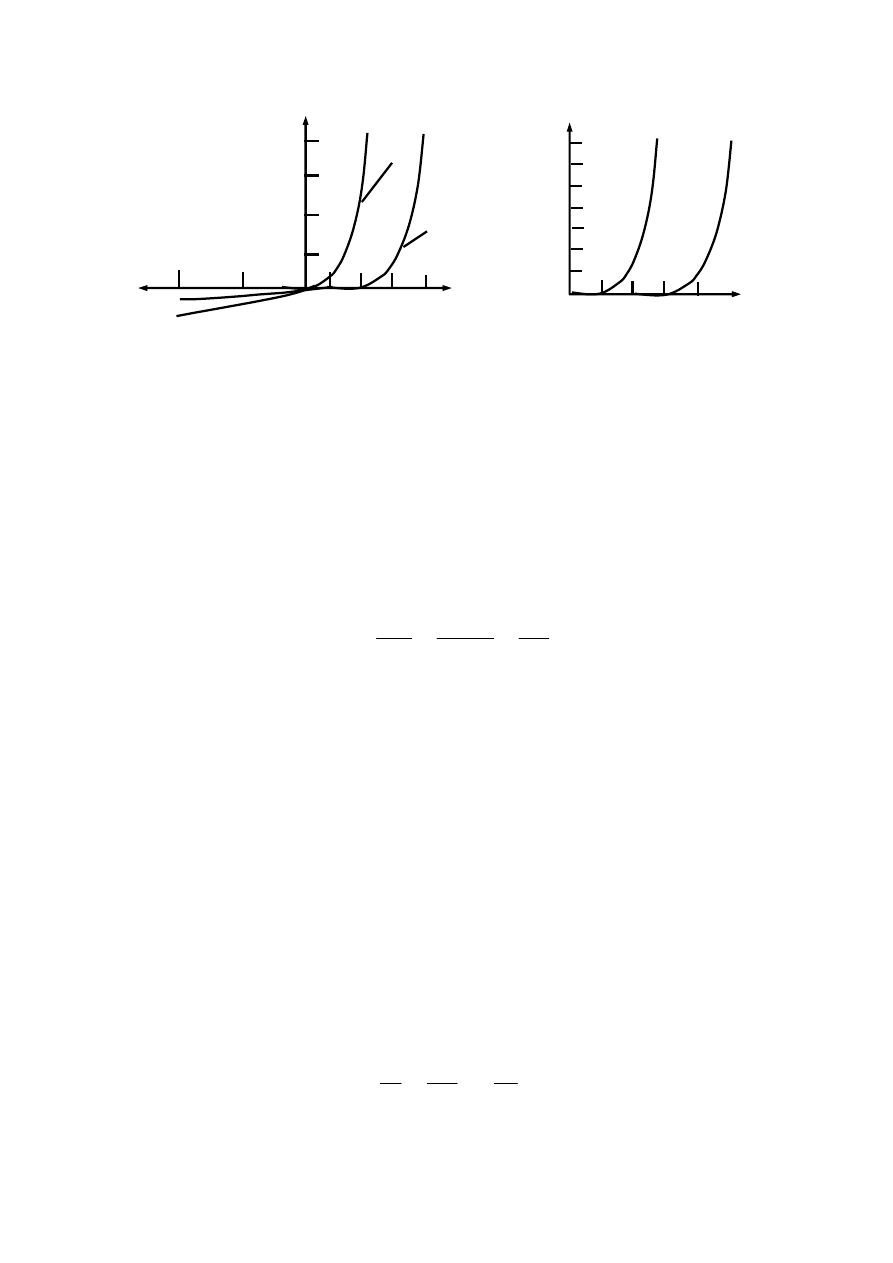
Рис. 2.13 — Характеристики идеализированных диодов с разными
площадями переходов (а) и разными тепловыми токами —
германиевого и кремниевого (б)
Как
и
в
ламповой
технике
,
различают
дифференциальные
сопротивления
и
сопротивления
постоянному
току
.
Найдя
производную
от
функции
(2.26),
легко
представить
дифференциальное
сопротивление
как
функцию
тока
(
рис
. 2.14, а)
0
.
T
T
Д
dU
r
dI
I
I
I
ϕ
ϕ
=
=
≈
+
(2.28)
Приближенное
выражение
,
разумеется
,
действительно
толь
-
ко
для
прямой
ветви
при
условии
0
I
I
>> .
На
обратной
ветви
ве
-
личина
Д
r
резко
возрастает
,
а
на
прямой
ветви
величина
Д
r
,
на
-
оборот
,
быстро
уменьшается
.
При
таком
сопротивлении
измене
-
ние
прямого
напряжения
даже
на
5–10 мВ
приводит
к
значитель
-
ным
изменениям
тока
.
Поэтому
задать
прямое
напряжение
с
це
-
лью
получить
нужный
ток
весьма
трудно
,
и
для
полупроводнико
-
вого
диода
,
работающего
в
прямом
направлении
,
более
характе
-
рен
режим
генератора
тока
.
На
это
указывалось
при
выводе
фор
-
мулы
(2.27).
Часто
при
расчете
диодных
схем
пользуются
сопро
-
тивлением
постоянному
току
—
статическое
сопротивление
.
Из
формулы
(2.23)
получаем
зависимость
такого
сопротивления
от
тока
(
рис
. 2.14, а)
0
ln
1 .
T
Д
U
I
R
I
I
I
⎛
⎞
ϕ
=
=
+
⎜
⎟
⎝
⎠
(2.29
а
)