Файл: задания по ВМиПП в матлабе.pdf

19 

2.1.2  Основные  элементы  схем  замещения  электрических  цепей  постоян-

ного тока 

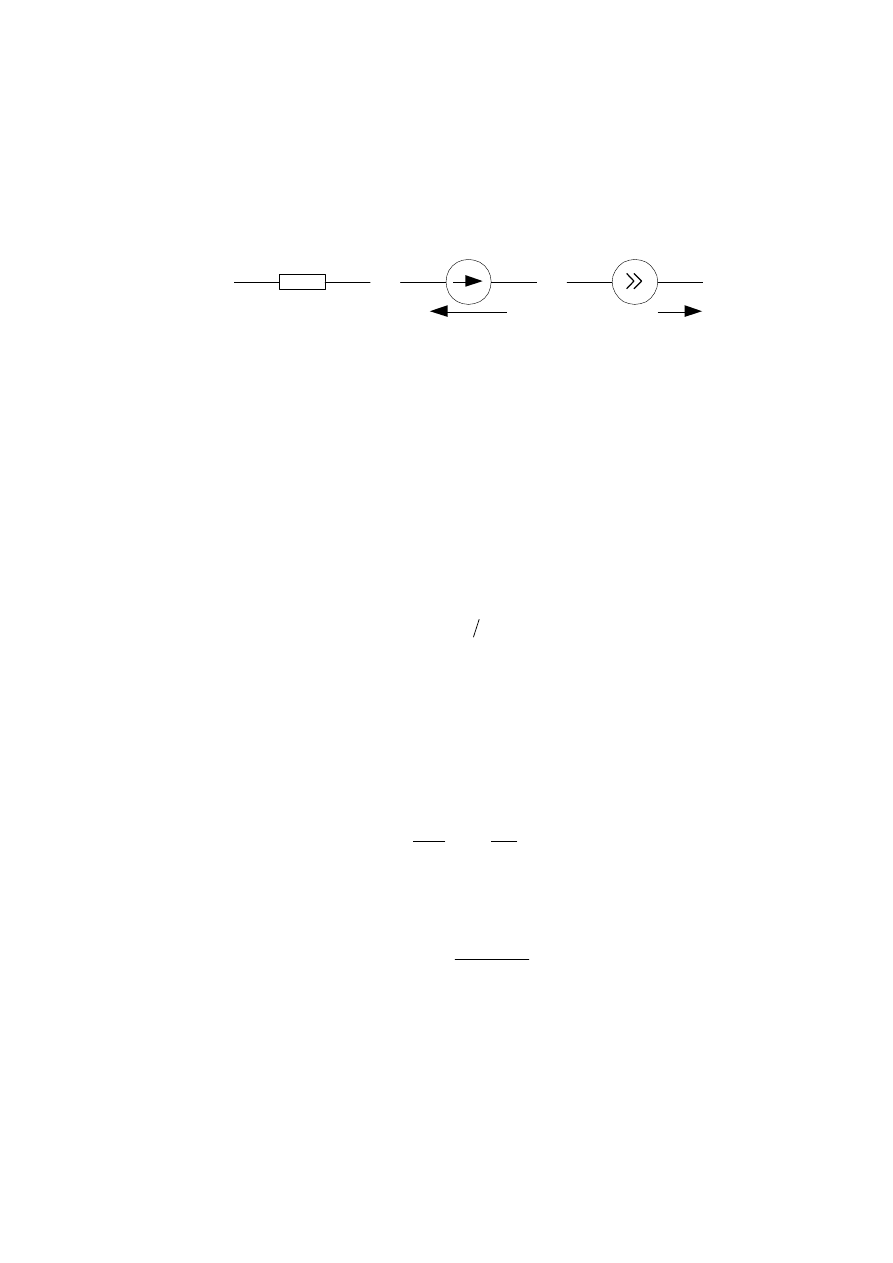
В схемах замещения на постоянном токе используют следующие основные 

элементы, показанные на рисунке 2.2, сопротивление (1), идеальный источник 
ЭДС (2), идеальный источник тока (3). 

R

E

J

1

2

3

U

I

Рисунок 2.2 - Основные элементы схем замещения на постоянном токе 

 
Идеальное  сопротивление  -  сопротивление  характеризует  свойство  про-

водника  поглощать  энергию  из  электрической  цепи  и  преобразовывать  ее  в 
другие  виды  энергии  (в  основном  в  тепловую).  Единица  измерения  сопротив-
ления – ом (Ом). Для участка цепи с сопротивлением r ток и напряжение связа-
ны простым соотношением – законом Ома: 

I

R

U





. 

Величина, обратная сопротивлению, называется проводимостью:  

R

1

g



. 

Единица измерения проводимости – сименс (См). 
Электротехническое  устройство,  обладающее  сопротивлением,  называют 

резистором. Регулируемый резистор (резистор с изменяемым сопротивлением) 
называется реостатом.  

При параллельном соединении n ветвей с сопротивлениями Ri эквивалент-

ное сопротивление этой цепи находится по формуле: 









n

i

1

i

i

Э

R

1

R

1

. 

Для  распространенного  случая  параллельного  соединения  двух  сопротив-

лений: 

2

1

2

1

Э

R

R

R

R

R







. 

Эквивалентное  сопротивление  последовательно  включенных  элементов 

цепи равно сумме сопротивлений отдельных элементов. 

Идеальный источник ЭДС 
Идеальный источник ЭДС имеет неизменные ЭДС и напряжение на зажи-

мах при всех токах нагрузки. У реального источника ЭДС и напряжение на за-

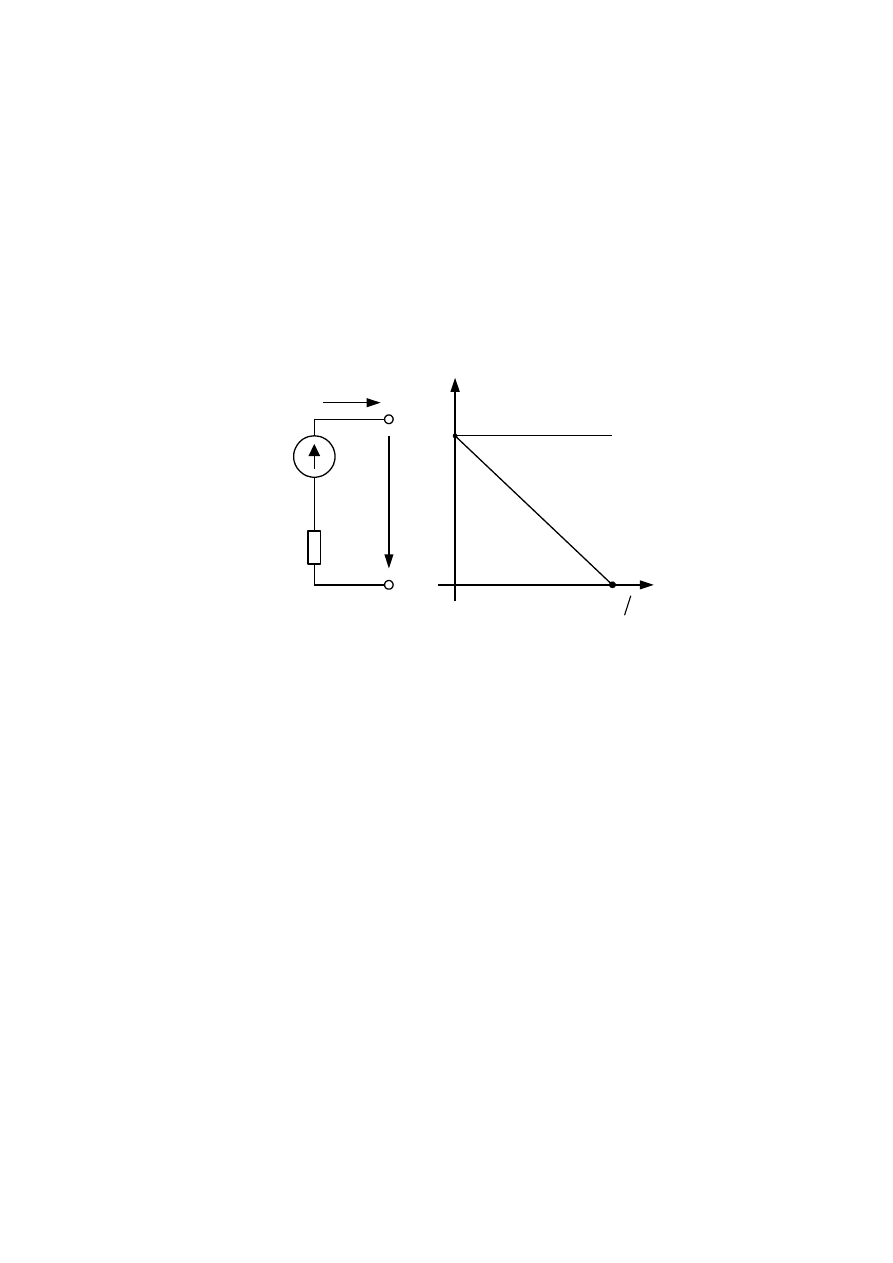
20 

жимах изменяются при изменении нагрузки, например вследствие падения на-
пряжения  в  обмотках  генератора  постоянного  тока.  Поэтому  реальные  источ-
ники  ЭДС  изображается  с  помощью  двух  последовательно  включенных  эле-
ментов  –  идеального  источника  ЭДС  и  сопротивления,  которое  учитывает 
внутреннее  сопротивление  реального  источника  (рисунок  2.3  а).  Свойства  ре-
ального  источника  ЭДС  отражает  вольт-амперная  характеристика  (ВАХ)  или 
внешняя характеристика – зависимость напряжения между его выводами от то-
ка  источника  (рисунок  2.3  б).  Уравнение  внешней  характеристики  реального 
источника ЭДС: 

I

r

E

U







. 

Е

r

U

I

U

I

Е

Идеальная 

ВАХ

Ре

ал

ьн

ая

 ВА

Х

r

E

I

КЗ



а

б

Рисунок 2.3. Схема замещения (а) и внешняя  характеристика(б) реального 

источника ЭДС 

Уменьшение  напряжения  источника  электрической  энергии  при  увеличе-

нии тока объясняется увеличением падения напряжения на его внутреннем со-
противлении.  В  большинстве  случаев  внутреннее  сопротивление  источника 
ЭДС  относительно  мало  и  напряжение  на  его  зажимах  мало  изменяется  с  на-
грузкой.  

Идеальный источник тока обеспечивает протекание неизменного тока в 

приемниках  при  изменении  их  сопротивления.  У  реального  источника  ток  во 
внешней  цепи  изменяется  при  изменении  сопротивления.  Поэтому  реальный 
источник  тока  изображается  на  схемах  как  идеальный  источник  тока  с  парал-
лельно  включенным  сопротивлением,  величина  которого  определяется  из  ха-
рактеристики элемента (рисунок 2.4 а). Внешняя характеристика источника то-
ка приведена на рисунке 2.4 б.  

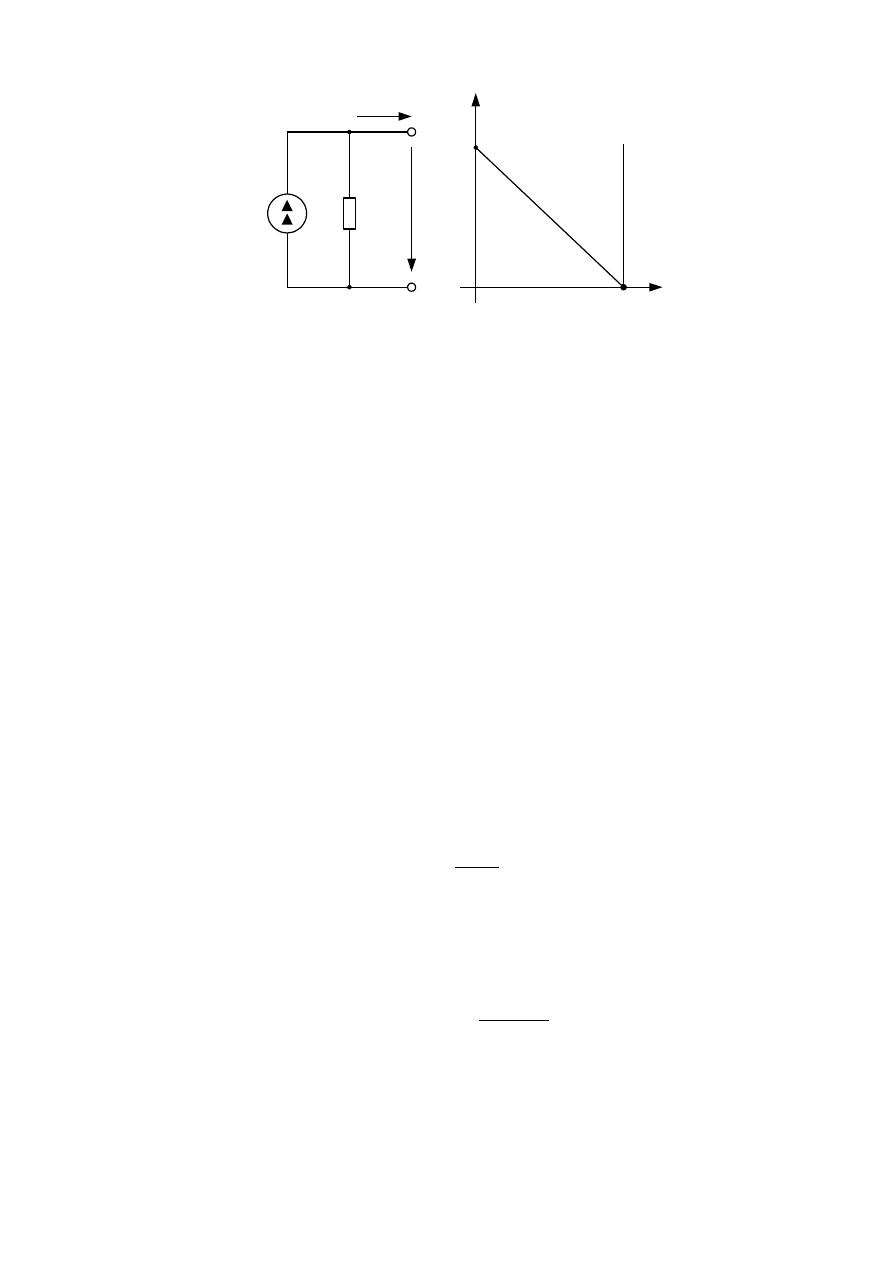
21 

I

U

J

r

U

I

I

И

д

е

ал

ьн

ая

В

А

Х

Ре

ал

ьн

ая

 ВА

Х

r

I

U

XX





б

а

Рисунок 2.4 Схема замещения (а) и внешняя характеристика (б) реального 

источника тока 

Различают несколько режимов работы источников энергии. В режиме хо-

лостого  хода  приемники  электрической  энергии  отключены  и  ток  источника 
равен нулю. Напряжение на зажимах источника равно его ЭДС, так как отсут-
ствует падение напряжения на внутреннем сопротивлении. Короткое замыка-
ние является аварийным режимом, когда зажимы источника энергии замкнуты 
накоротко. При этом ток в цепи определяется только внутренним сопротивле-
нием источника, которое обычно достаточно мало, поэтому токи короткого за-
мыкания достигают недопустимо больших значений. В номинальном режиме 
источник  энергии  может  работать  неопределенно  длительное  время  без  пере-
грева  или  других  недопустимых  последствий.  Согласованный  режим  работы 
осуществляется,  когда  источник  отдает  в  нагрузку  максимальную  мощность. 
Условие передачи максимальной мощности может быть получено из уравнения 
внешней характеристики источника: 

I

r

I

r

I

r

U

E

H















, 

если выразить из этого уравнения ток нагрузки: 

r

r

E

I

H





, 

получим закон Ома для замкнутой цепи с последовательной схемой замещения 
источника.  Мощность,  отдаваемая  источником  ЭДС  (с  последовательной  схе-
мой замещения) в нагрузку: 





2

H

2

H

2

H

r

r

E

r

I

r

P











. 

Для источника тока (с параллельной схемой замещения) мощность, отдаваемая 
в нагрузку: 

22 





2

H

2

2

H

2

H

r

r

I

r

r

I

r

P













. 

Мощность,  отдаваемая  источником  в  нагрузку  будет  максимальна,  при 

максимальном  значении  соотношения 





2

H

H

r

r

r



.  Максимум  этого  соотношения 

можно определить, взяв первую производную дроби по  

r

 и приравняв ее к ну-

лю. Максимум будет при 

H

r

r



. Следовательно, мощность, отдаваемая источни-

ком во внешнюю цепь будет максимальна, когда сопротивление внешней цепи 

H

r

 равно внутреннему сопротивлению источника 

r

. 

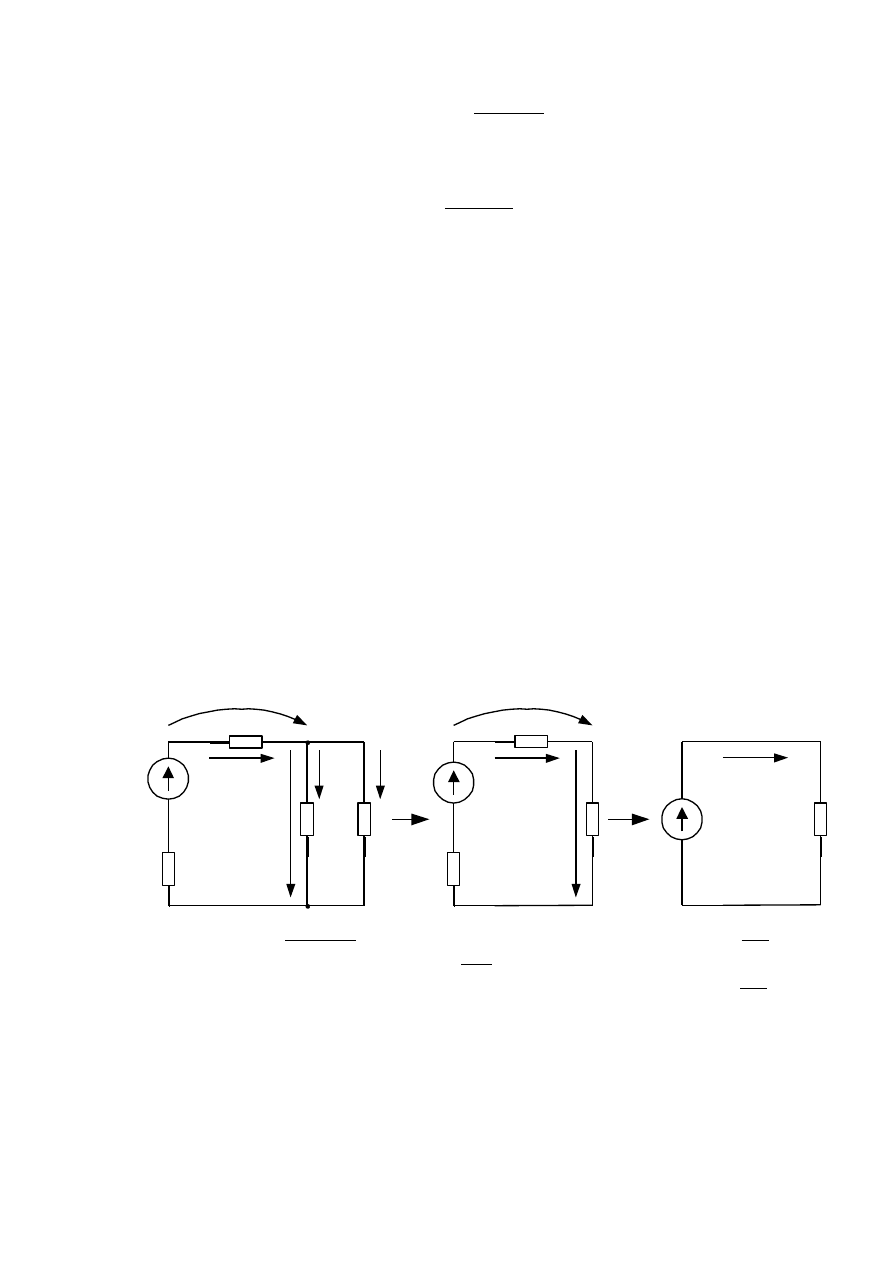
2.1.3 Методы расчета электрических цепей 
2.1.3.1 Метод эквивалентных преобразований 

Для  расчета простых  электрических цепей с  одним источником  часто ис-

пользуется  метод  эквивалентных  преобразований.  Суть  метода  заключается  в 
том, что отдельные  участки схемы  с последовательно или параллельно соеди-
ненными  элементами  заменяют  одним  эквивалентным  элементом.  Постепен-
ным  преобразованием  участков  схему  упрощают  и  приводят  к  простей  про-
стейшей  схеме  состоящей  из  источника  и  одного  эквивалентного  элемента. 
Пример  расчета  схемы  методом  эквивалентного  преобразования  приведен  на 
рисунке 2.5. 

Е

r

R1

R2

R3

I1

I2

I3

U2

U1

Е

r

R1

R23

I1

U2

U1

Е

Rэ

I1

3

2

3

2

23

R

R

R

R

R







r

R

R

R

1

23

Э







Э

1

R

E

I



1

1

1

R

I

U





23

1

2

R

I

U





2

2

2

R

U

I



3

2

3

R

U

I



Рисунок 2.5 - Пример расчета схемы методом 

эквивалентных преобразований 

23 

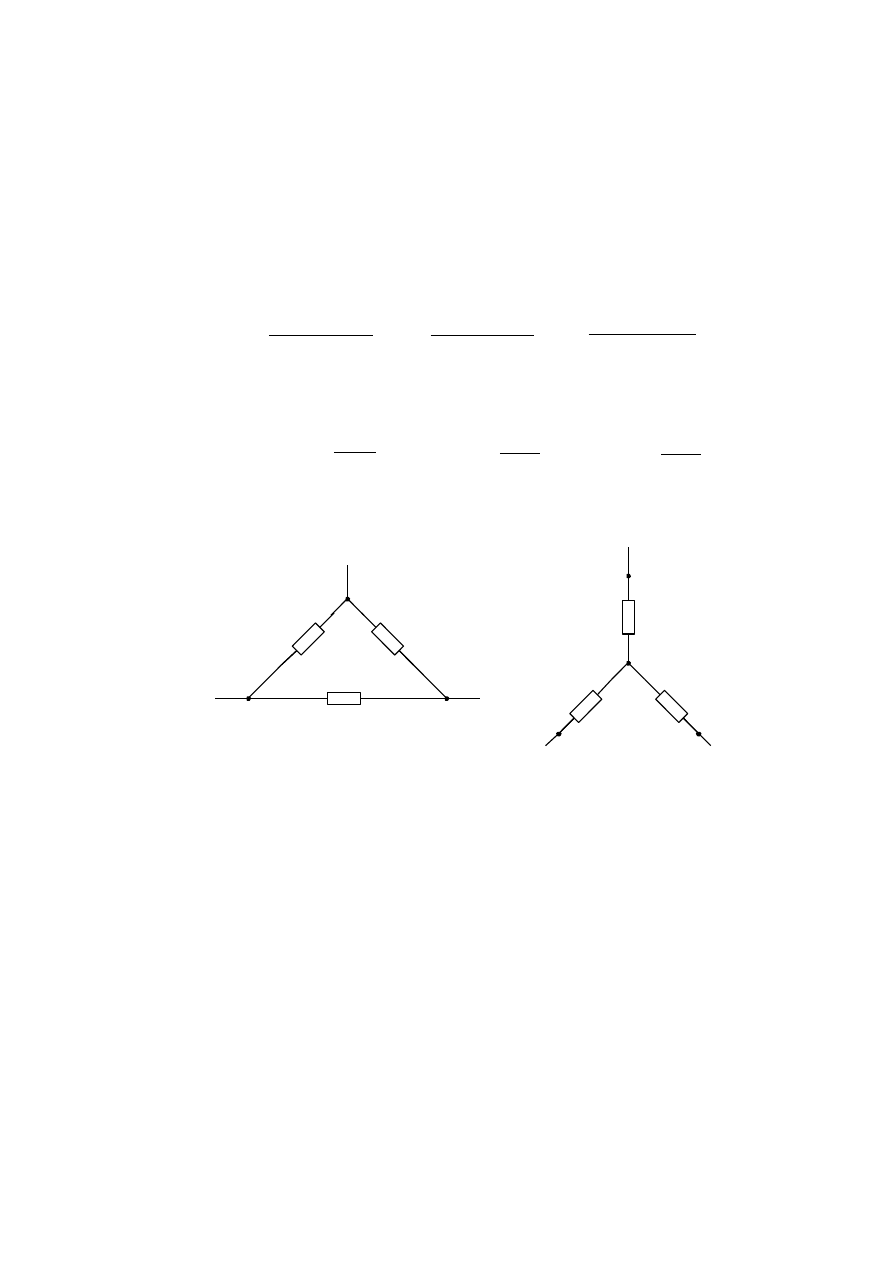
Встречаются  схемы  со  сложным  соединением  элементов,  которые  нельзя 

отнести ни к последовательному, ни к параллельному соединению. Рассмотрим 
одну из таких схем, когда часть ее образует треугольник, вершинами которого 
являются  три узла, а сторонами три сопротивления, включенные между этими 
узлами (рисунок 2.6 а). Для упрощения подобных схем во многих случаях бы-
вает  удобно  заменить  треугольник  эквивалентной  трехлучевой  звездой  (рису-
нок  2.6  б).  В  этом  случае  эквивалентные  сопротивления  звезды  находятся  по 
формулам: 

ca

bc

ab

ca

ab

a

r

r

r

r

r

r









,  

ca

bc

ab

ab

bc

b

r

r

r

r

r

r









, 

ca

bc

ab

bc

ca

c

r

r

r

r

r

r









. 

При  замене  трехлучевой  звезды  эквивалентным  треугольником  сопротив-

ление резисторов треугольника можно определить по формулам: 

c

b

a

b

a

ab

r

r

r

r

r

r









,  

a

c

b

c

b

bc

r

r

r

r

r

r









,  

b

a

c

a

c

ca

r

r

r

r

r

r









. 

А

B

C

А

B

C

BC

r

AB

r

CA

r

A

r

B

r

C

r

а

б

Рисунок 2.6 – Схемы соединения нагрузок 

 
На рисунке 2.7 показана схема, для которой переход от звезды резисторов 

a

r

, 

b

r

, 

c

r

 к эквивалентному треугольнику, позволяет получить цепь с простым 

смешанным соединением и использовать метод эквивалентных преобразований 
для расчета схемы.