Файл: задания по ВМиПП в матлабе.pdf

24 

Rca

R1

Rbc

R2

Rab

E

r

Ra

R1

Rc

R2

Rb

E

r

a

b

c

a

b

c

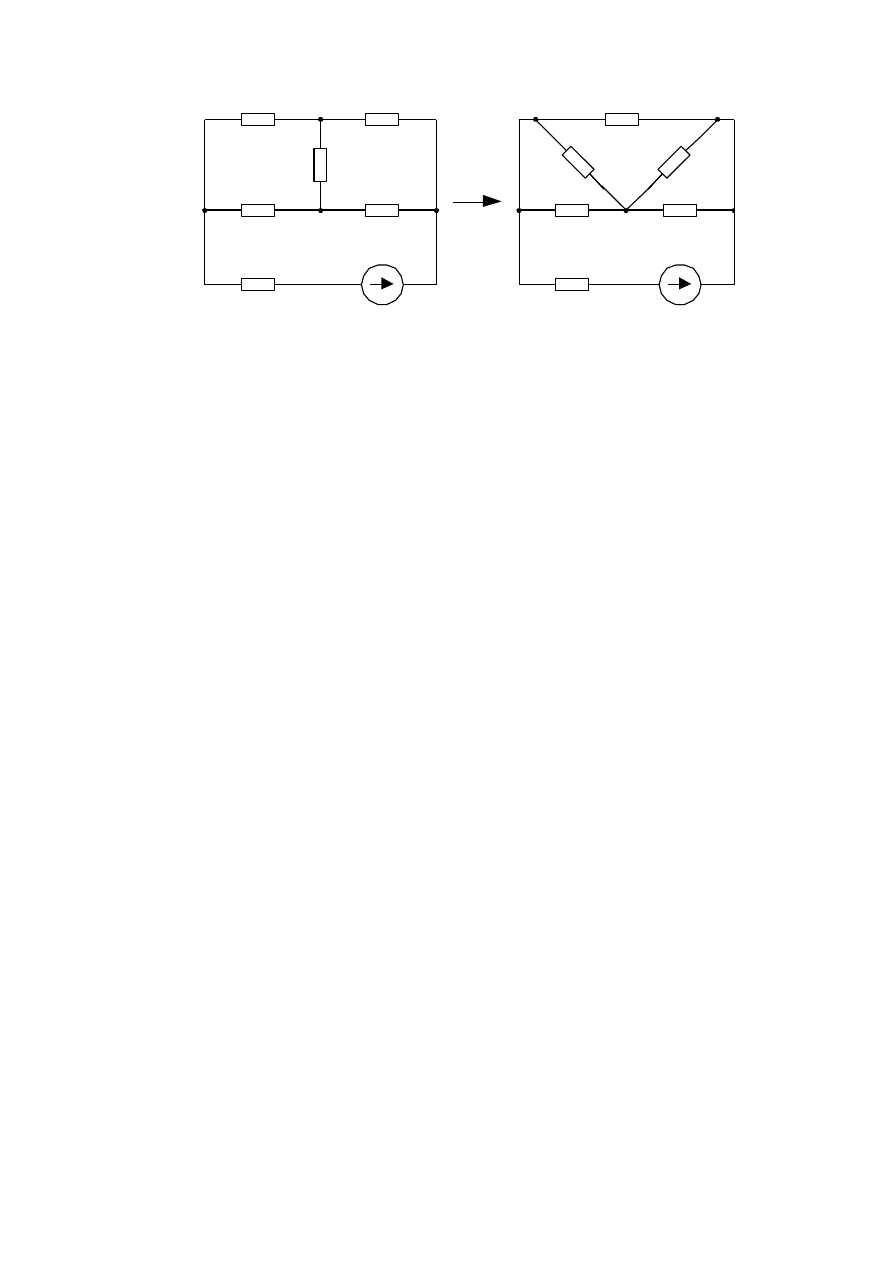
Рисунок 2.7 - Замена звезды эквивалентным треугольником 

2.1.3.2 Расчет электрических цепей с помощью законов Кирхгофа 

Для анализа разветвленных электрических цепей в электротехнике приме-

няются  законы  Кирхгофа,  выражающие  два  основных  свойства  электрических 
цепей. Согласно первому закону Кирхгофа алгебраическая сумма токов ветвей, 
сходящихся в узле, равна нулю: 







n

1

k

k

0

I

. 

При этом токи, направленные к узлу берут с одним произвольным знаком, 

а направленные от узла с противоположным. 

По второму закону Кирхгофа алгебраическая сумма напряжений на участ-

ках (резистивных элементах) замкнутого контура равна алгебраической сумме 
ЭДС: 



















m

1

k

k

n

1

k

k

k

n

1

k

Rk

E

I

r

U

, 

где m – число источников ЭДС в контуре, n – число резистивных элементов в 
контуре. 

При этом напряжения, положительные направления которых совпадают с 

направлением  обхода,  берут  с  положительными  знаками, а  напряжения, поло-
жительные направления которых противоположны направлению обхода – с от-
рицательными знаками. 

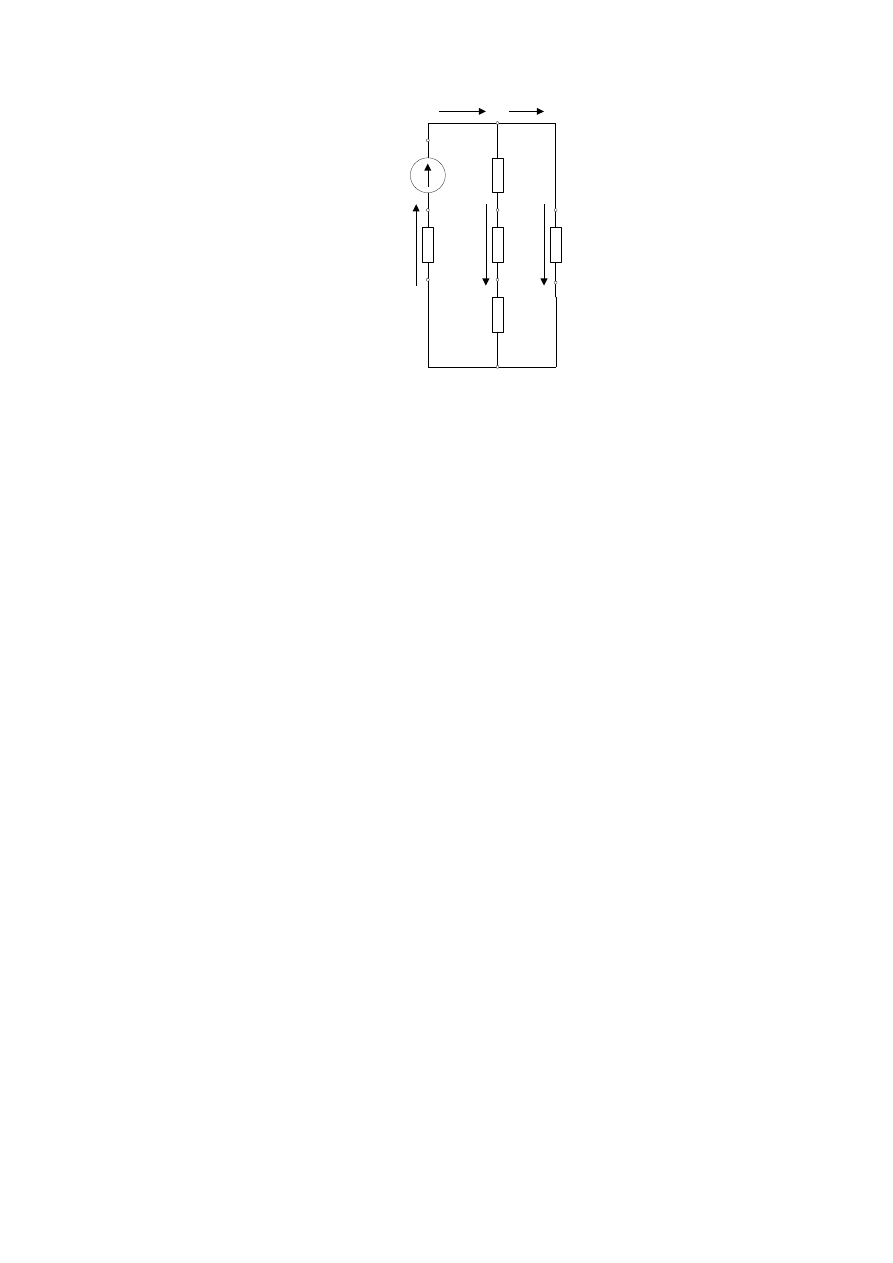
 Для  примера  рассмотрим  электрическую  схему  на  рисунке  2.8.  На  схеме 

имеются три ветви (между точками 1-3, 4-7, 8-9), три независимых контура (1-
8-9-3-2-1, 1-4-5-6-7-3-2-1, 4-8-9-7-6-5-4), два узла (4, 7).  

25 

R1

R2

R3

R4

R5

E1

I1

I2

I3

I1

I3

1

2

3

4

5

6

7

8

9

Рисунок 2.8 -  Пример применения  

законов Кирхгофа 

 
Запишем уравнение, реализующее первый закон Кирхгофа для узла 4: 

0

I

I

I

3

2

1







. 

Уравнение, реализующее второй закон Кирхгофа для контура 1-8-9-3-2-1: 

1

5

3

1

1

E

R

I

R

I









. 

Для контура 1-4-5-6-7-3-2-1 уравнение по второму закону Кирхгофа: 

1

4

3

2

2

1

1

E

)

R

R

R

(

I

R

I













. 

Для нахождения токов в схеме необходимо составить систему из m уравнений, 
где m – число неизвестных токов, равное числу ветвей схемы. Порядок расчета 
электрических схем с помощью законов Кирхгофа   должен быть следующий: 



Обозначить условно положительные направления токов на схеме. 



Составить (n – 1) – уравнений по первому закону Кирхгофа, где n – 

число узлов в схеме.  



Так  как  число  неизвестных  токов  в  схеме  равно  числу  ее  ветвей,  а 

число ветвей всегда больше числа узлов, то недостающие уравнения составля-
ют по второму закону Кирхгофа. 

 С  помощью  законов  Кирхгофа  можно  рассчитывать  цепи  любой  сложно-

сти, однако для сложных схем с несколькими источниками система  уравнений 
получается  слишком  громоздкой.  Для  расчета  таких  схем  применяют  другие 
методы расчета. 

2.1.3.3 Метод двух узлов 

В случае, когда в электрической схеме несколько источников ЭДС и цепь 

состоит из n параллельных ветвей и имеет всего два узла, расчет  проще всего 

26 

проводить при помощи метода двух узлов. По этому методу сначала определя-
ют напряжение между двумя узлами схемы, а потом находят токи ветвей. На-
чинают с выбора условно положительного направления напряжения между уз-
лами  и  обозначают  его  стрелкой  на  схеме.  Напряжение  между  двумя  узлами 
параллельной цепи равно алгебраической сумме произведений проводимости и 
ЭДС каждой ветви, деленной на сумму проводимостей всех ветвей схемы.  

















n

k

1

k

k

m

k

1

k

k

k

АВ

g

E

g

U

; 

Уравнение записано для цепи имеющей n ветвей, m из которых активные, 

то есть содержат источники ЭДС. Произведение проводимости и ЭДС берут со 
знаком "плюс" в том случае, когда направление ЭДС противоположно выбран-
ному условно положительному направлению напряжения между двумя узлами 
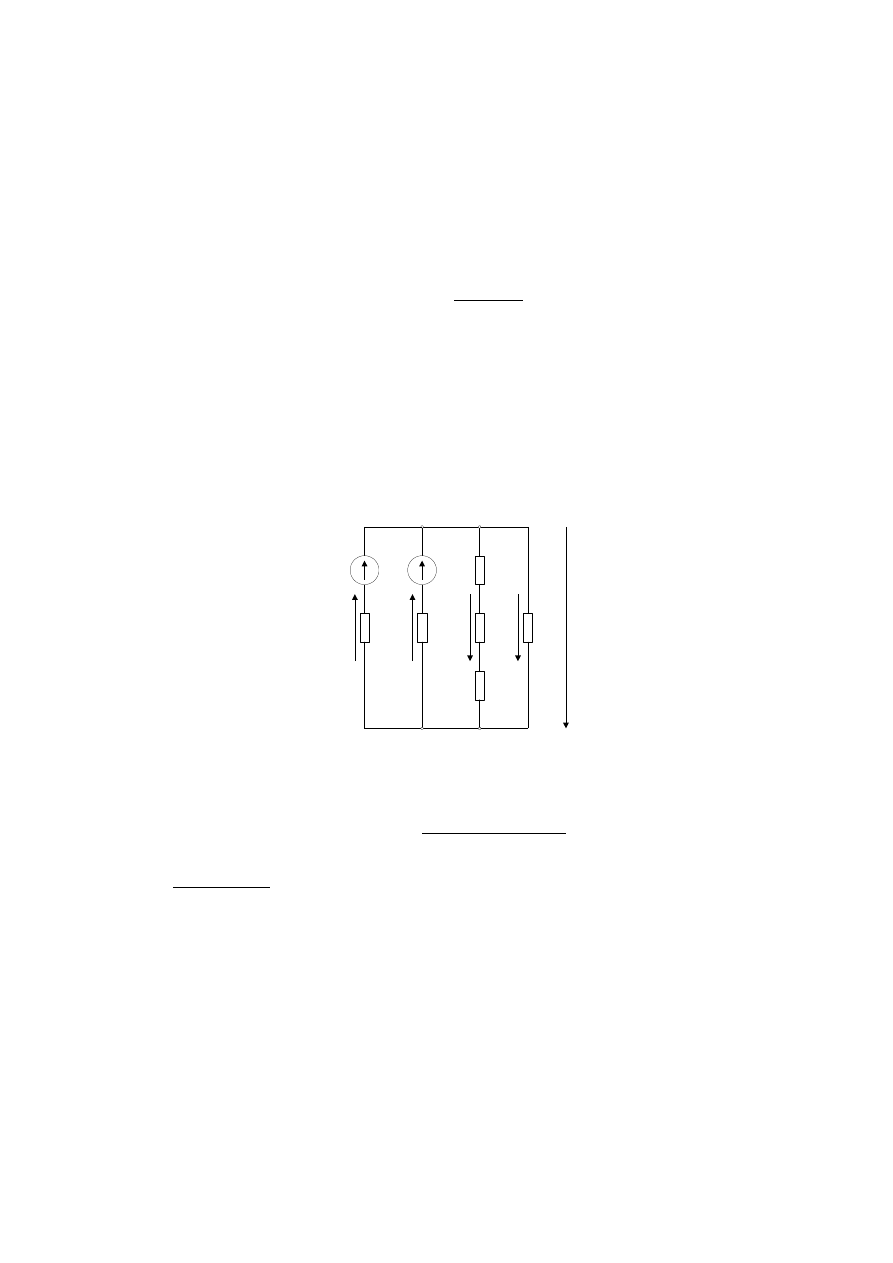
и со знаком "минус", когда эти направления совпадают. Для примера рассмот-
рим схему на рисунке 2.9. 

R1

R2

R3

R4

R5

E1

I1

I2

I3

R6

I4

E2

Uab

a

b

Рисунок 2.9 - Пример применения метода двух узлов 

Уравнение, записанное по методу двух узлов для этой схемы: 

6

5

234

1

1

1

2

6

АВ

g

g

g

g

E

g

E

g

U















где 

4

3

2

234

R

R

R

1

g







 - эквивалентная проводимость последовательно включен-

ных сопротивлений. 

2.1.3.4 Метод наложения 

Метод наложения используется для расчета сложных цепей с несколькими 

источниками питания. Суть этого метода заключается в том, что расчет слож-
ной цепи с несколькими источниками сводят к расчету нескольких цепей с од-
ним источником. Ток в любой ветви исходной схемы является результатом на-
ложения  токов,  получающихся  от  отдельных  источников  ЭДС,  действующих 
независимо друг от друга. 

27 

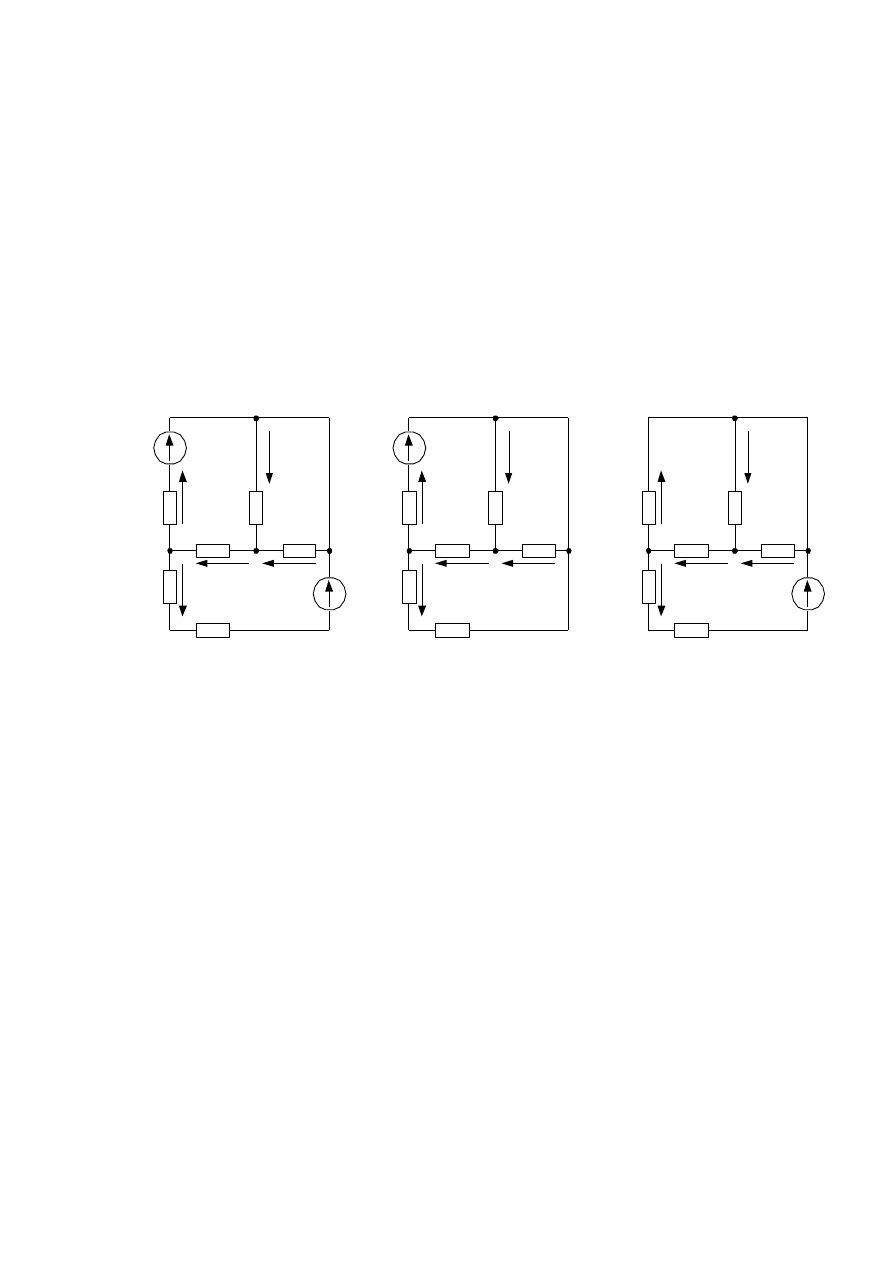
 Для примера рассмотрим цепь с двумя источниками на рисунке 2.10 а. Для 

определения токов в схеме методом наложения, вначале полагают, что в схеме 

действует только источник 

1

Е

. При этом сопротивления всех резисторов, вклю-

чая  внутреннее  сопротивление  источника 

2

Е

,  считается  неизменным.  Опреде-

ление частичных токов схемы от ЭДС 

1

Е

 (

1

I



,

2

I



…

n

I



) сводится к расчету цепи на 

рисунке 2.10 б. Далее повторяют расчет для ЭДС 

2

Е

 (рисунок 2.10 в), и находят 

частичные токи 

1

I



,

2

I



…

n

I



. Алгебраическое суммирование частичных токов дает 

действительное  значение  токов  ветвей: 

1

1

1

I

I

I









,   

2

2

2

I

I

I









…

n

n

n

I

I

I









.  При 

этом число слагаемых в последних уравнениях будет равно числу источников 
ЭДС в схеме.  

R1

R2

R3

R4

R5

R6

E1

E2

I1

I2

I3

I5

I4

R1

R2

R3

R4

R5

R6

E1

I1'

I2'

I3'

I5'

I4'

R1

R3

R4

R5

R6

E2

I1''

I2''

I3''

I5''

I4''

а

б

в

Рисунок  2. 10 - Расчет  электрической цепи методом наложения 

2.1.3.5 Метод эквивалентного генератора 

В некоторых случаях бывает необходимо проанализировать режим работы 

одной  из  ветвей  сложной  электрической  цепи  при  изменении  сопротивления 
этой же ветви.  При этом целесообразно воспользоваться методом эквивалент-
ного генератора. Согласно этому методу воздействие всех источников электри-
ческой  цепи  на  исследуемую  ветвь  можно  заменить  воздействием  последова-
тельно  соединенного  с  ветвью  эквивалентного  генератора,  имеющего  ЭДС 

ЭКВ

Е

 и внутреннее сопротивление 

ЭКВ

r

.  

Для  определения  параметров  эквивалентного  генератора,  исследуемую 

ветвь отключают от остальной схемы и с помощью любого известного метода 
расчета  находят  напряжение  на  зажимах  схемы,  к  которым  была  подключена 
исследуемая  ветвь.  Таким  образом,  определяется  напряжение  холостого  хода 

эквивалентного  генератора,  равное его  ЭДС 

ЭКВ

Е

.  Для  определения  внутрен-

28 

него  сопротивления  эквивалентного  генератора 

ЭКВ

r

,  определяют  эквивалент-

ное сопротивление схемы относительно зажимов, к которым была подключена 
исследуемая ветвь. Зная ЭДС и внутренне сопротивление эквивалентного гене-
ратора, можно определить ток в исследуемой ветви: 

R

r

E

I

ЭКВ

ЭКВ





, 

где R – сопротивление исследуемой ветви. 

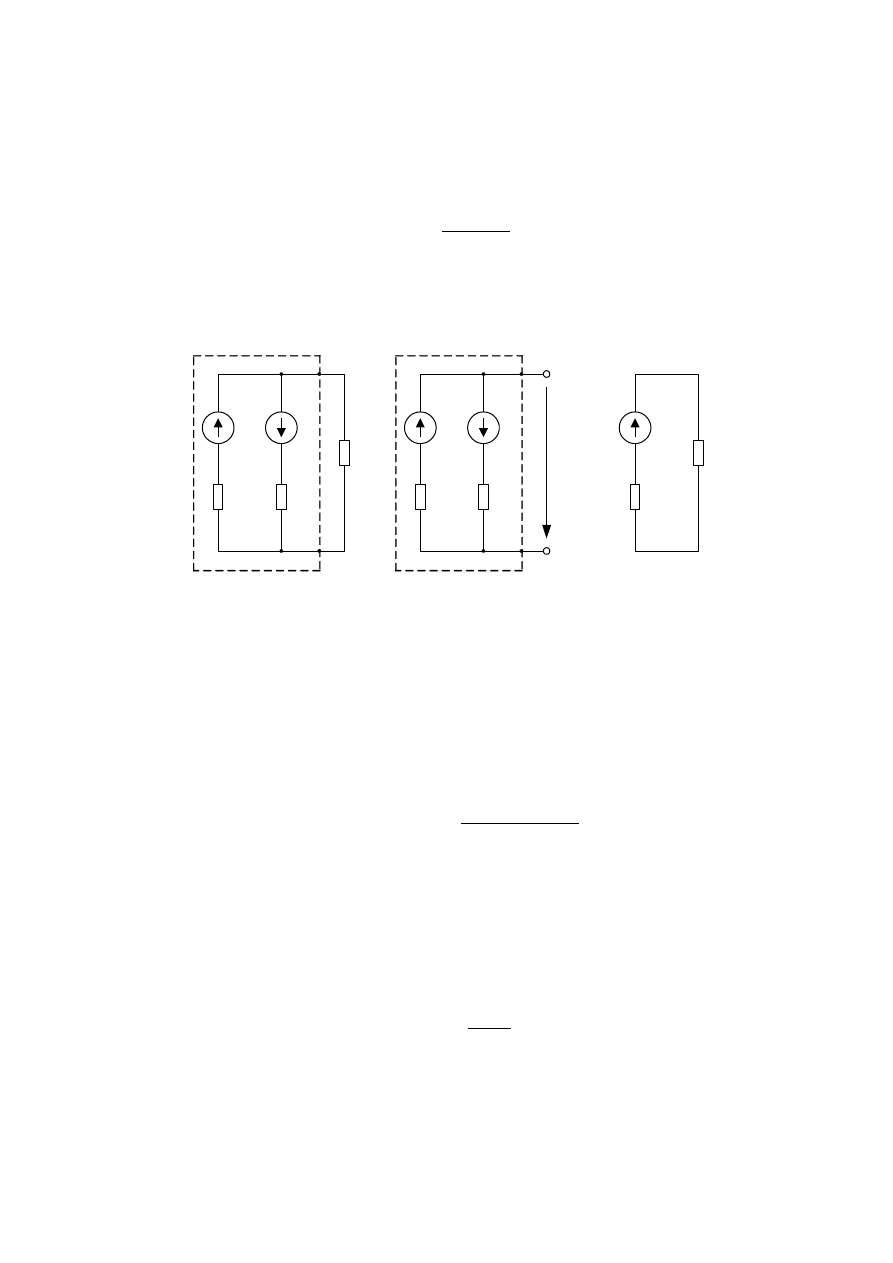
Рассмотрим  применение  метода  эквивалентного  генератора  на  примере 

схемы на рисунке 2.11 а. 

Е1

Е2

r1

r2

R

а

б

Е2

r2

а

б

U

абх

r1

Е1

Еэкв

r

экв

R

а

б

в

Рисунок 2.11 - Применение метода эквивалентного генератора 

В схеме исследуемая ветвь с сопротивлением R подключена к зажимам "а" 

и "б". Отключив ветвь с сопротивлением R от схемы необходимо найти напря-

жение  на  зажимах  "а"  и  "б"    -

абх

U

,  равное  ЭДС  эквивалентного  генератора. 

Удобнее всего это сделать с помощью метода двух узлов: 

2

1

2

2

1

1

ЭКВ

абх

G

G

E

G

E

G

Е

U













. 

Внутреннее  сопротивление  эквивалентного  генератора  равно  сопротивле-

нию схемы между зажимами "а" и "б" схемы рисунке 2.11 б. Так как внутреннее 
сопротивление идеальных источников ЭДС равно нулю, то внутреннее сопро-
тивление генератора равно эквивалентному сопротивлению параллельно вклю-

ченных сопротивлений 

1

r

 и 

2

r

: 

2

1

2

1

ЭКВ

r

r

r

r

r







.