Криволинейная корреляция

Если линейная аппроксимация статистической зависимости между двумя величинами не отражает характер зависимости, используют модель криволинейной корреляции. Одной из распространенных является параболическая корреляция второго порядка, при которой уравнение регрессии Y на X имеет вид:

.

На практике выборка совместного распределения случайных величин X и Y возникает как последовательность пар перечисленных в порядке произведенных наблюдений, среди них могут быть и одинаковые. Для нахождения коэффициентов регрессии не обязательно группировать данные в корреляционную таблицу.

Как и в случае линейной корреляции, коэффициенты регрессии найдем из условия минимума функционала:

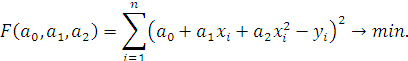
Условием минимума является обращение в нуль частных производных:

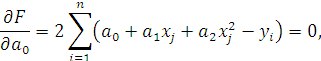
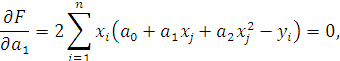
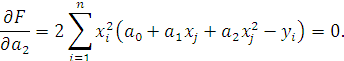
Это дает систему трех линейных уравнений относительно трех неизвестных которая называется системой нормальных уравнений:

Решая ее, получаем уравнение регрессии.

Отметим, что если ввести матрицу А и векторы у и а:

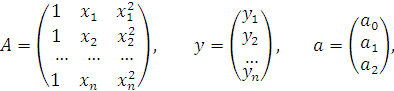
то в матричном виде систему нормальных уравнений можно записать как

А'Аа = А'у,

где А' – матрица, получаемая из матрицы А транспонированием.

Такая запись системы нормальных уравнений облегчает ее запоминание. Она переносится и на рассматриваемую далее множественную корреляцию.

Пример. Желая установить цену на товар, обеспечивающую максимальную прибыль, магазин в течении 5 рабочих дней недели продавал получаемые от поставщика изделия с наценкой 1, 2, 3, 4 и 5 у.е. При этом в каждый из дней было продано соответственно 100, 80, 60, 30 и 10 единиц товара. С помощью модели параболической регрессии второго порядка выбрать надбавку, дающую максимальную прибыль.

Решение. Выпишем таблицу соответствия между наценкой и полученной прибылью, определяемой как произведение наценки на количество проданного товара.

наценка Х	1	2	3	4	5
прибыль Y	100	160	180	120	50

Заметим, что устанавливаемая оценка по смыслу является величиной неслучайной. Прибыль, определяемая количеством проданного товара, напротив, величина случайная, среднее значение которой зависит от наценки. Уравнение регрессии Y на X ищем в виде:

Из полученной таблицы находим коэффициенты системы нормальных уравнений:

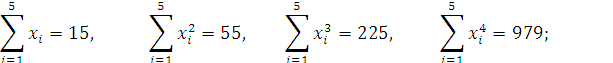
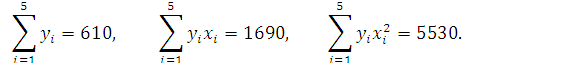
Система нормальных уравнений запишется в виде:

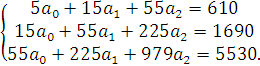
Произведя сокращение на 5, получим систему:

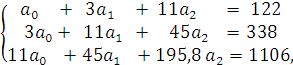
которую будем решать методом Гаусса.

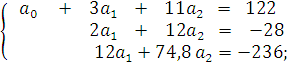
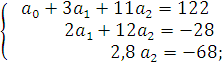
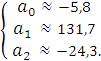
Выборочное уравнение регрессии примет вид:

Даваемая моделью оптимальная наценка равна

а получаемая при такой наценке средняя ежедневная прибыль

Вычисленная по модели максимальная средняя ежедневная прибыль оказалась несколько меньше прибыли, полученной в день, когда наценка была равна 3. Это не должно вызывать недоумения. Согласно модели этот день был скорее случайной удачей, чем правилом.

---

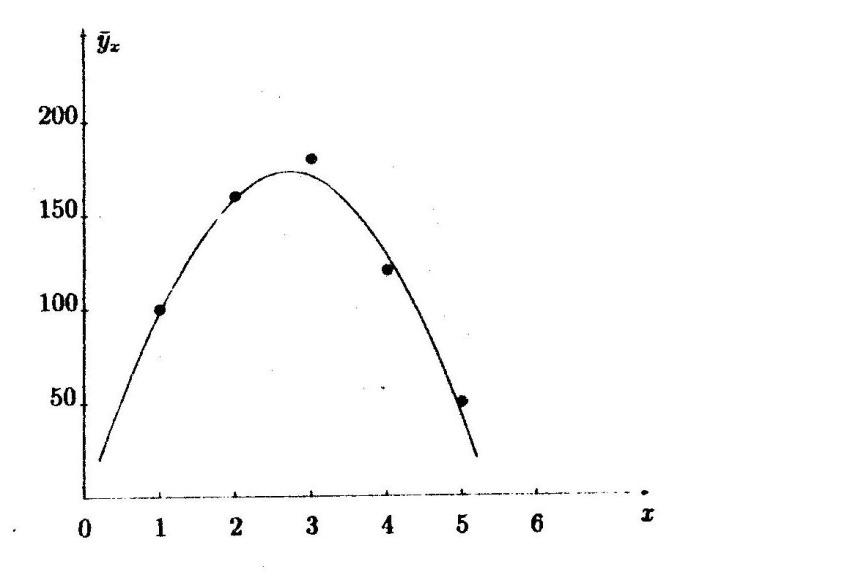
На графике представлены значения полученных прибылей при различных наценках и полученная по ним параболическая линия регрессии.

---

Смотрите также файлы

• Лекция 5. Элементы теории корреляции.doc

• Лекция 4. Неодинаковое число испытаний на различных уровнях.doc

• Лекция 3. Общая, факторная и остаточная дисперсии.doc

• Лекция 2. Элементы дисперсионного анализа.doc

• Лекция 1. Графический способ обработки опытных данных.doc