ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса
Категория: Лекция
Дисциплина: Методы обработки экспериментальных данных
Добавлен: 29.10.2018
Просмотров: 488
Скачиваний: 34
Множественная корреляция
Пусть случайная
величина Y
зависит от величин ![]() Такую корреляцию называют множественной.
Уравнение линейной множественной
регрессии ищется в виде:
Такую корреляцию называют множественной.
Уравнение линейной множественной
регрессии ищется в виде:
![]() .
.
Используемая
выборка состоит из n
наборов ![]() соответствующих
значений
соответствующих
значений ![]() величины Y,
где
величины Y,
где ![]() Коэффициенты
Коэффициенты ![]()
![]() находятся по выборке методом наименьших
квадратов.
находятся по выборке методом наименьших
квадратов.
Как и в случае
линейной парной регрессии, средние
значения ![]() должны удовлетворять этом уравнению:
должны удовлетворять этом уравнению:
![]() .
.
Это позволяет,
исключив коэффициент ![]() ,
записать уравнение регрессии в виде:
,
записать уравнение регрессии в виде:
![]()
Такая запись уравнения весьма удобна и позволяет понизить на единицу порядок системы нормальных уравнений.
Пример.
В течение 7 месяцев фирма давала рекламу
своего товара по телевидению и в печати.
Ежемесячные расходы на рекламу (![]() ,
а также доход фирмы от продажи товара
(Y)
в тыс. у.е. сведены в таблице:
,
а также доход фирмы от продажи товара
(Y)
в тыс. у.е. сведены в таблице:
|
|
|
Y |
|
100 |
100 |
500 |
|
140 |
100 |
550 |
|
100 |
140 |
570 |
|
120 |
120 |
570 |
|
140 |
100 |
560 |
|
100 |
140 |
580 |
|
140 |
140 |
590 |
Получить по таблице уравнение регрессии
![]() ,
,
на основании которого предложить эффективную рекламную политику.
Решение. Уравнение регрессии будем искать в виде
![]()
Из таблицы находим:
![]() Переопределенная
система линейных уравнений, даваемая
выборкой, примет вид:
Переопределенная
система линейных уравнений, даваемая
выборкой, примет вид:
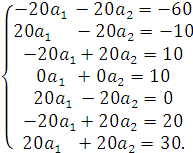
После сокращения и удаления уравнения, не содержащего неизвестных, получаем:
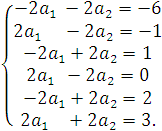
Соответствующая нормальная система запишется в виде:
![]()
Ее решение: ![]() Полученные значения коэффициентов
регрессии свидетельствуют о том, что
реклама по телевидению убыточна
Полученные значения коэффициентов
регрессии свидетельствуют о том, что
реклама по телевидению убыточна ![]() ,
а реклама в печати, наоборот, приносит
некоторый доход
,
а реклама в печати, наоборот, приносит
некоторый доход ![]() .
Поэтому
относительно среднего уровня
.
Поэтому
относительно среднего уровня ![]() вложения в рекламу по телевидению
следует снизить, направив освободившиеся
средства на рекламу в печати.
вложения в рекламу по телевидению
следует снизить, направив освободившиеся
средства на рекламу в печати.
4.Метод наименьших квадратов
Пусть
величина Y
является линейной комбинацией величин
![]()
![]()
неизвестные
коэффициенты ![]() которой нужно найти. Для этого величинам
которой нужно найти. Для этого величинам
![]() придается
n
наборов значений и измеряются
соответствующие значения Y.
Это дает для определения
придается
n
наборов значений и измеряются
соответствующие значения Y.
Это дает для определения ![]() следующую систему линейных уравнений:
следующую систему линейных уравнений:
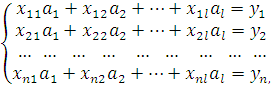
где
![]() обозначает значение величины
обозначает значение величины ![]() в
в ![]()
Минимальное
число необходимых для этого уравнений
n
равно l.
Если определитель системы отличен от
нуля, что обычно и имеет место на практике,
то система имеет при ![]() единственное
решение. Если же число уравнений n
больше числа неизвестных l,
то так как любые n
из уравнений системы являются независимыми,
а остальные
единственное
решение. Если же число уравнений n
больше числа неизвестных l,
то так как любые n
из уравнений системы являются независимыми,
а остальные ![]() – их следствиями, теоретически можно
выбрать любую подсистему из l
уравнений
и решить ее. На практике, однако, каждое
измерение величины Y
неизбежно связано с погрешностью. Это
приводит к тому, что система при
– их следствиями, теоретически можно
выбрать любую подсистему из l
уравнений
и решить ее. На практике, однако, каждое
измерение величины Y
неизбежно связано с погрешностью. Это
приводит к тому, что система при ![]() оказывается несовместной. Если же из
нее выбрать подсистему из l
уравнений, то полученные значения
коэффициентов
оказывается несовместной. Если же из
нее выбрать подсистему из l
уравнений, то полученные значения
коэффициентов ![]() будут зависеть от этого выбора.
будут зависеть от этого выбора.
Для разрешения данной ситуации еще в начале XIX века немецким математиком Гауссом и французским математиком Лежандром был предложен прием, получивший название метода наименьших квадратов, который стал одним из основных способов обработки экспериментальных данных. Фактически, этот прием уже использовался нами при определении коэффициентов линейной и параболической парной корреляции. Теперь этот важный метод будет рассмотрен в общем виде.
Уравнения
системы пытаются удовлетворить
приближенно. В качестве меры близости
берется сумма квадратичных уклонений
левых частей от свободных членов.
Решением по методу наименьших квадратов
называется набор ![]() ,
доставляющий минимум функционала
,
доставляющий минимум функционала
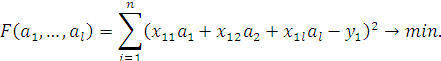
Отметим,
что если система допускает точное
решение, то минимальное значение F
оказывается равным нулю, и решение по
методу наименьших квадратов является
точным решением. Практически же для
более точного нахождения неизвестных
коэффициентов систему стараются
переопределить как можно сильнее,
увеличивая число уравнений n.
Если ошибку в измерении величины Y
считать, как обычно делается в теории
ошибок, нормально распределенной
случайной величиной с нулевым
математическим ожиданием, то такой
метод может быть обоснован теоретически
как доставляющий значения ![]() ,
наиболее близкие к их действительным
значениям.
,
наиболее близкие к их действительным
значениям.
Условия минимума F является равенство нулю частных производных:
![]()
что
дает для определения ![]() систему
l
линейных уравнений с l
неизвестными,
которая называется системой
нормальных уравнений.
систему
l
линейных уравнений с l
неизвестными,
которая называется системой
нормальных уравнений.
Если ввести матрицу A исходной системы уравнений, вектор-столбец свободных членов y и вектор-столбец неизвестных a:
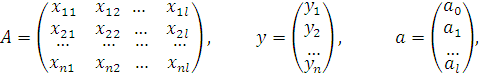
то в матричном виде систему нормальных уравнений можно записать как
![]()
где
![]() матрица,
получаемая из матрицы A
транспонированием.
матрица,
получаемая из матрицы A
транспонированием.
Матрица
![]() нормальной системы является квадратной
симметрической
нормальной системы является квадратной
симметрической ![]() матрицей.
Ее
матрицей.
Ее ![]() элементы равны скалярному произведению
i-го
и j-го
столбцов матрицы A.
элементы равны скалярному произведению
i-го
и j-го
столбцов матрицы A.
Пример:
Дана система точек, координаты которых
указаны в таблице, число точек ![]()
|
x |
|
0 |
1 |
2 |
3 |
4 |
|
y |
0 |
2 |
3 |
3,5 |
3 |
4,5 |
Требуется
построить прямую с уравнением ![]() .
.
Решение: Очевидно, что точки с данными координатами не могут быть расположены на одной прямой, а построить прямую как бы «сглаживающую» эти точки, можно. Для этого достаточно решить систему уравнений, приведенную в соответствующей теоретической части. Для удобства расчетов строим рабочую таблицу:
|
№ |
|
|
|
|
|
|
|
|
1 |
|
0 |
1 |
0 |
0,81 |
0,81 |
0,6561 |
|
2 |
0 |
2 |
0 |
0 |
1,55 |
|
0,2025 |
|
3 |
1 |
3 |
1 |
3 |
2,29 |
|
0,5041 |
|
4 |
2 |
3,5 |
4 |
7 |
3,03 |
|
0,2209 |
|
5 |
3 |
3 |
9 |
9 |
3,77 |
0,77 |
0,5929 |
|
6 |
4 |
4,5 |
16 |
18 |
4,51 |
0,01 |
0,0001 |
|
|
9 |
16 |
31 |
37 |
|
|
2,1766 |
|
|
|
|
|
|
|
|
|
Первый
столбец обозначает номер по порядку
записи точек (координат). Из сумм столбцов
при ![]() составляются коэффициенты системы
составляются коэффициенты системы
![]()
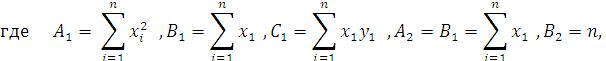
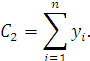
Для
определения параметров ![]() прямой
прямой ![]() Система имеет вид:
Система имеет вид:
![]()
Решим ее методом определений:
![]()
![]()
Искомое
уравнение ![]()