Добавлен: 19.10.2018
Просмотров: 4036
Скачиваний: 59
СОДЕРЖАНИЕ
1.Исследование функции на безусловный экстремум
2. Численные методы безусловной минимизации
Метод конфигураций (Хука-Дживса)
Метод деформируемого многогранника (Нелдера-Мида)
Метод наискорейшего градиентного спуска
Метод сопряженных направлений (Флетчера – Ривса)
Порядок выполнения лабораторной работы
Пример выполнения лабораторной работы
3. Решение задачи минимизации со смешанными ограничениями
Седловые точки функции Лагранжа
Метод седловой точки в задачах квадратичного программирования
Метод проекции градиента для задачи условной оптимизации
Метод условного градиента для задачи условной оптимизации
Метод возможных направлений для задачи условной оптимизации
Порядок выполнения лабораторной работы
Пример выполнения лабораторной работы
4. Основные понятия линейного программирования
Модель задачи линейного программирования
Свойства задачи линейного программирования
Двойственность в линейном программировании
Построение модели транспортной задачи
Методы нахождения начального плана перевозок.
Задание 2. Числовые характеристики симметричной квадратной матрицы.
Задание 3. Формула Тейлора для функции нескольких переменных
Задание 4. Нахождение локальных экстремумов
Задание 5. Одномерная оптимизация
Задание 6. Многомерная оптимизация по направлению
Задание 7. Методы безусловной оптимизации
Задание 8. Методы условной оптимизации
Задание 9. Задача линейного программирования и симплекс-метод
Задание 10. Транспортная задача
Пример выполнения лабораторной работы
Функция:
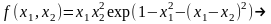 min,
x0=(-2,-2).
min,
x0=(-2,-2).
Методы: градиентного спуска и Ньютона.
Решение.
Примечание: при построении графика используется среда MathCAD 12.1. 1. Построим график функции и линии уровня.
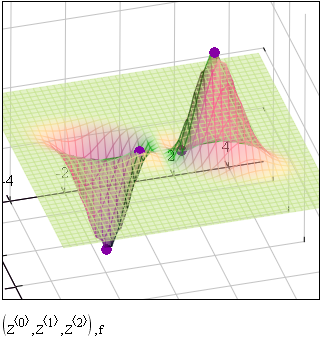
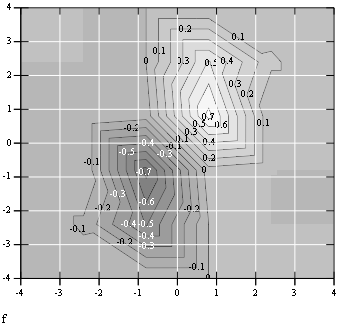
2. Решим задачу минимизации аналитически.
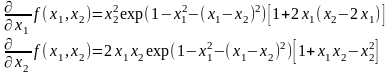
Система для нахождения стационарных точек из условия равенства нулю градиента имеет вид
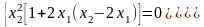
Если x1x2 =0
то из системы следует, что x1 =0 и x2 =0
Первая стационарная точка – A0(0;0).
Если x1x2 ≠0:
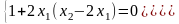
Подставим
х1
в первое уравнение:
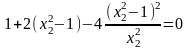
Введем
замену
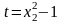 :
:
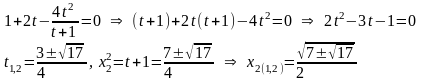
Обозначим
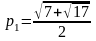 ,
,
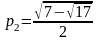 .
.
Получаем остальные стационарные точки:
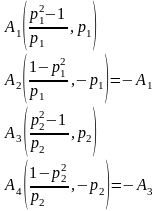
Приближенные числовые координаты найденных точек:
А0(0;0), А1(1.068;1.668), А2(-1.068;-1.668), А3(-0.331;0.848), А4(0.331;-0.848).
Построим и исследуем на знакоопределенность матрицу Гессе в точках А0,…,А4.
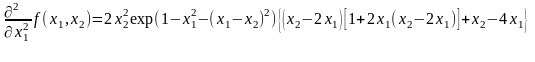
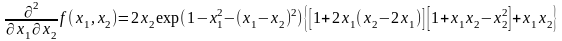
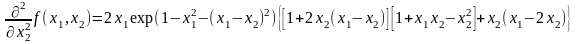
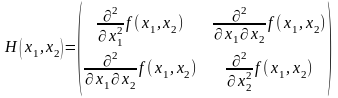
H(A0(0;0))=0
(требуется дополнительное исследование
точки).
Анализ поведения функции в окрестности точки A0(0;0) показывает, что, придавая х1 положительное и отрицательное значение при любом х2, можно получить соответственно положительное и отрицательное значение функции. Таким образом, A0(0;0) не является ни точкой локального минимума, ни точкой локального максимума.
Н(А1(1.068;1.668))≈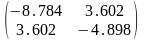 ,
отрицательно определена, в точке
локальный максимум.
,
отрицательно определена, в точке
локальный максимум.
Н(А2(-1.068;-1.668))≈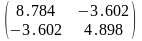 ,
положительно определена, в точке
локальный минимум.
,
положительно определена, в точке
локальный минимум.
Н(А3(-0.331;0.848))≈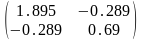 ,
положительно определена, в точке
локальный минимум.
,
положительно определена, в точке
локальный минимум.
Н(А4(0.331;-0.848))
≈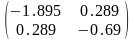 ,
отрицательно определена, в точке
локальный максимум.
,
отрицательно определена, в точке
локальный максимум.
Точками глобального экстремума являются А1(1.068;1.668) – глобальный максимум, f (A1) ≈1.801; А2(-1.068;-1.668)– глобальный минимум, f (A2) ≈-1.801.
3. Остальные задания реализованы на языке СИ, для чего написаны классы для работы с векторами и матрицами (CVector и CMatrix) и использующее их приложение. В методе наискорейшего спуска для одномерной минимизации используется метод золотого сечения. Для отыскания собственных чисел матрицы Гессе применяется метод Якоби, для построения обратной матрицы – метод Жордана-Гаусса.
В начале работы программа выводит информацию о стационарных точках:
Stationary dots:
x1 x2 f(x1,x2) Extreme
1.067890 1.667566 1.801131 LOC MAX
-1.067890 -1.667566 -1.801131 LOC MIN
-0.331077 0.848071 -0.144426 LOC MIN
0.331077 -0.848071 0.144426 LOC MAX
GLOBAL MIN: x(-1.067890, -1.667566)
f(x) = -1.801131
GLOBAL MAX: x(1.067890, 1.667566)
f(x) = 1.801131
Затем устанавливается начальная точка x0(-2,-2), функция исследуется на выпуклость/вогнутость в этой точке, выводится число обусловленности матрицы Гессе:
x0(-2.000000, -2.000000) Hessian: Alternating sign
f(x0) = -0.398297
cond H(x0) = 4.751665
Таким образом, квадратичная форма, соответствующая матрице Н(-2,-2), является знакопеременной. Функция не является “овражной” в окрестности точки, и допустимо применение метода градиентного спуска.
Далее запускается метод наискорейшего градиентного спуска, и выполняются 2 итерации.
Steepest
descent method:
x2(-1.200031,
-1.706888) Hessian: Convex
grad_f(x2)
= (-0.963083, 0.275166)
f(x2)
= -1.741440
В
результате 2 итераций мы получили точку,
достаточно близкую к точке глобального
минимума.
Теперь
из точки
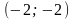 стартует метод Ньютона с
поправкой гессиана.
Результат
двух
итераций:
стартует метод Ньютона с
поправкой гессиана.
Результат
двух
итераций:
Newton method:
x2(-2.735431, -2.306328) Hessian: Alternating sign
grad_f(x2) = (-0.110421, 0.031948)
f(x2) = -0.018516
Видно, что метод расходится. Начальная точка выбрана неудачно; увеличение числа итераций приводит к дальнейшему расхождению метода. Это объясняется тем, что метод Ньютона применим в окрестности точки минимума.
Анализируя
линии уровня функции, выберем начальную
точку ближе к оптимальной. Например,
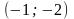 :
:
x0(-1.000000, -2.000000) Hessian: Convex
f(x0) = -1.471518
cond H(x0) = 3.786885
Newton method:
x2(-1.047041, -1.722604) Hessian: Convex
grad_f(x2) = (0.379214, -0.339841)
f(x2) = -1.787758
Как
в начальной, так и в конечной точке
функция является выпуклой. За две
итерации мы приблизились к точке
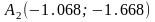 .
.
Теперь
возьмем начальную точку еще ближе к
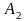 ,
например
,
например
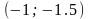 :
:
x0(-1.000000, -1.500000) Hessian: Convex
f(x0) = -1.752302
cond H(x0) = 3.857905
Newton method:
x2(-1.067889, -1.667566) Hessian: Convex
grad_f(x2) = (0.000000, 0.000000)
f(x2) = -1.801131
Метод Ньютона достиг точки глобального минимума, об этом говорит практически нулевой вектор-градиент.
Точное
значение
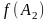 отличается от найденного
отличается от найденного
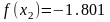 на 4.729∙10-7(по
модулю).
на 4.729∙10-7(по
модулю).
В лабораторной работе проведено исследование заданной функции на глобальный экстремум с использованием аналитических преобразований, графика функции и разработанного приложения на языке C++.
С помощью метода градиентного спуска удалось улучшить целевую функцию без каких-либо дополнительных действий. Метод Ньютона при выборе в качестве начальной точки x0(-2,-2) не сошелся. Проблема была решена заменой начальной точки на более подходящую для данного метода. Это позволило за две итерации прийти в точку глобального минимума. Полученные результаты хорошо согласуются с теорией.
Разработанные классы CVector и CMatrix могут применяться в будущих проектах.
3. Решение задачи минимизации со смешанными ограничениями
Общая задача нахождения экстремума функции при наличии ограничений - равенств и ограничений - неравенств записывается в следующем виде:
f(x)→ extr, (5)
xX= {xEn: gi(x)≤0, i=1,2,...,r; gi(x)=0, i=r+1, ..., m, m-r<n},
где среди функций f(x) и gi(x) могут быть нелинейные.
Активные ограничения – неравенства в точке х* ─ это ограничения, которые выполняются в данной точке в виде равенства.
Пассивные ограничения – неравенства в точке х* ─ это ограничения, которые выполняются в данной точке в виде строгого неравенства.
Если градиенты активных ограничений-неравенств и ограничений-равенств в точке х* линейно независимы, то говорят, что в оптимальной точке выполнено условие регулярности.
Обобщенная функция Лагранжа для задачи со смешанными ограничениями задается как
L(x,λ0,λ)=λ0f(x)+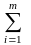 λigi(x)
(6)
λigi(x)
(6)
В
случае регулярности
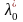 ≠0,
и можно положить этот коэффициент равным
1.
≠0,
и можно положить этот коэффициент равным
1.
Теорема Куна – Таккера (дифференциальная форма необходимого условия минимума)
Пусть
точка х*
- точка локального минимума в задаче
математического программирования (5),
функции
f,gr+1,...,gm
дважды непрерывно дифференцируемы в
точке х,
функции g1,...,gr
дважды непрерывно дифференцируемы в
некоторой окрестности точки x.
Тогда существует число
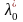 и
вектор
и
вектор
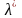 такие, что выполняются следующие условия:
такие, что выполняются следующие условия:
-
условие стационарности обобщенной функции Лагранжа по х:
gradxL(x*,
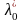 ,
,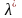 )=0
)=0
-
условие нетривиальности:
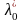 2+
2+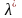 2>0
2>0
то есть, хотя бы один из множителей Лагранжа отличен от нуля;
-
условие неотрицательности:
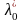 ≥0,
≥0,
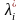 ≥0,
i=1,
...,
r,
≥0,
i=1,
...,
r,
то есть, множители Лагранжа, соответствующие целевой функции и ограничениям – неравенствам, неотрицательны;
-
условия дополняющей нежесткости:
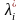 gi(x*)=0,
i=1,
2, ...,
r
gi(x*)=0,
i=1,
2, ...,
r
Если при этом выполнено условие регулярности, то справедливо следующее Утверждение: Если функции f, gr+1,..., gm выпуклые, а функции g1,..., gr – линейные, то условия теоремы Куна – Таккера являются одновременно и достаточными условиями глобального минимума.
Достаточное условие минимума первого порядка:
Пусть
имеется точка (х*,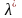 ),
удовлетворяющая условию стационарности
обобщенной функции Лагранжа по х
при
),
удовлетворяющая условию стационарности
обобщенной функции Лагранжа по х
при
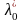 ≠0,
суммарное число активных ограничений-неравенств
в точке х*
и ограничений-равенств совпадает с
числом переменных n.
Если
≠0,
суммарное число активных ограничений-неравенств
в точке х*
и ограничений-равенств совпадает с
числом переменных n.
Если
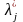 >0
для всех активных ограничений gj(x),
то точка х*
- точка условного локального минимума
в задаче (5).
>0
для всех активных ограничений gj(x),
то точка х*
- точка условного локального минимума
в задаче (5).
Достаточное условие минимума второго порядка:
Пусть
имеется точка (х*,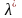 ),
удовлетворяющая условию стационарности
обобщенной функции Лагранжа по х
при
),
удовлетворяющая условию стационарности
обобщенной функции Лагранжа по х
при
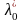 ≠0.
Если в этой точке d2L(х*,
≠0.
Если в этой точке d2L(х*,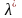 )>0
для всех ненулевых dx
таких, что для активных в точке х*
ограничений-неравенств dgj(x*)=0,
)>0
для всех ненулевых dx
таких, что для активных в точке х*
ограничений-неравенств dgj(x*)=0,
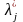 >0
и dgj(x*)≤0,
>0
и dgj(x*)≤0,
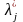 =0,
то точка х*
является точкой локального минимума.
=0,
то точка х*
является точкой локального минимума.
Общая схема решения задачи условной минимизации функции:
-
Составляется обобщенная функция Лагранжа вида (6).
-
Выписываются необходимые условия минимума, сформулированные в теореме Куна – Таккера. К этим условиям добавляются ограничения, задающие допустимое множество Х. Полученная система алгебраических уравнений и неравенств используется для поиска условно-стационарных (подозрительных на экстремум) точек. Целесообразно проанализировать отдельно случаи λ0=0 и λ0=1 (или λ0 – любое положительное число). Однако, если выполнено одно из условий регулярности, то вариант λ0=0 рассматривать не надо.
-
В найденных точках проверяется выполнение достаточных условий минимума и проводится анализ на глобальный экстремум.
Седловые точки функции Лагранжа
Существование экстремума тесно связано с наличием у функции Лагранжа (6) так называемой седловой точки.
Рассматривается задача выпуклого программирования с ограничениями-неравенствами
f(x)→ min, (7)
xX= {xEn: gi(x)≤0, i=1,2,..., m; х≥0},
Предполагается, что выполнено условие регулярности, то есть, можно рассматривать только вариант λ 0=1.
Определение
Точка
(х*,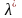 ),
где х*
Х,
),
где х*
Х,
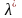 Еm,
Еm,
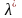 ≥0,
называется седловой точкой функции
Лагранжа L(x,λ),
если
≥0,
называется седловой точкой функции
Лагранжа L(x,λ),
если
L(x*,λ)≤
L(x*,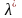 )≤
L(x,
)≤
L(x,
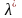 ) (8)
) (8)
Утверждение 1 (критерий для седловых точек функции Лагранжа).
Точка
(х*,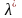 )–
является седловой для функции Лагранжа
L(x,λ)
в том и только том случае, когда выполнены
условия
)–
является седловой для функции Лагранжа
L(x,λ)
в том и только том случае, когда выполнены
условия
L(х*,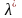 )=min
{L(x,
)=min
{L(x,
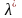 )׀
x
Х}, (9)
)׀
x
Х}, (9)
L(х*,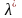 )=max
{L
(x*,λ)׀
λ
≥0}, (10)
)=max
{L
(x*,λ)׀
λ
≥0}, (10)
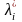 gi(x*)=0,
i=1,
2, ..., m.
(11)
gi(x*)=0,
i=1,
2, ..., m.
(11)
х*≥0
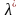 ≥0
≥0
Условие
(9) минимума функции Лагранжа по х
эквивалентно выполнению в точке (х*,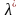 )
неравенства
)
неравенства
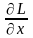 ≥0. (9′)
≥0. (9′)
Условие
(6) максимума функции Лагранжа по λ
эквивалентно выполнению в точке (х*,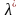 )
неравенства
)
неравенства
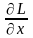 ≤0. (10′)
≤0. (10′)
Утверждение 2.
х*
- оптимальное решение задачи (3) в том и
только том случае, когда существует
такой вектор
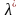 ≥0, что (х*,
≥0, что (х*,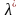 )
– седловая точка функции Лагранжа L
(x,λ).
)
– седловая точка функции Лагранжа L
(x,λ).
Метод седловой точки в задачах квадратичного программирования
Рассмотрим задачу квадратичного программирования, то есть,
f(x)=(Сx,x)
+(d,x)
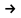 min (12)
min (12)
g(x)=Ax ≤ b,
где С – матрица размера n*n, d,х – векторы-столбцы n*1, А – матрица размера m*n, b – вектор-столбец m*1.
Для задачи квадратичного программирования критерий существования седловой точки приобретает вид задачи решения СЛАУ. Действительно:
Функция Лагранжа в этом случае запишется в виде
L
=
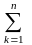 dkxk+
dkxk+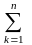
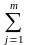 ckjxkxj+
ckjxkxj+
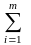 λi(
λi(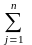 aijxj-bi),
(13)
aijxj-bi),
(13)
где ckj – элементы матрицы С, dk – элементы вектора d, bi – элементы вектора свободных членов b, aij – элементы матрицы А, λi – коэффициенты Лагранжа.
Необходимые и достаточные условия оптимальности решения х* принимают вид
vj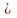 dj+2
dj+2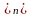 ckjxk+
ckjxk+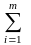 λiaij
, vj
≥0,
(j=1,...,n)
(14)
λiaij
, vj
≥0,
(j=1,...,n)
(14)
-yi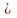
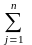 aijxj-bi
,
-yi
≤0,
(i=1,...,m) (15)
aijxj-bi
,
-yi
≤0,
(i=1,...,m) (15)
xjvj=0, xj≥0, (j=1,...,n) (16)
λi(-yi)=0, λi≥0 (17)
Равенства (14). (15) образуют систему n+m линейных уравнений с 2(n+m) неизвестными x1,...,xn,v1,...,vn, λ1,..., λm,y1,...,ym. Решения этой системы, при которых выполняются равенства (16), (17), дают координаты седловой точки (х*,λ*).
Чувствительность решения ЗНП
Пусть х*=х*(b) решение задачи нелинейного программирования
f(x)→ min, (13)
xX= {xEn: gi(x)≤bi, i=1,2,..., m; х≥0},
при некотором векторе b свободных членов в ограничениях – неравенствах, а v(b), соответственно, значение целевой функции при этом решении ЗНП, то есть, v(b)=f(x*). Тогда справедлива следующая оценка изменения целевой функции: ∆v=f(b+∆b)-f(b) при изменении вектора b на некоторый малый вектор-приращение ∆b:
∆f≈(∆b ,λ*), (14)
где λ* - вектор множителей Лагранжа, соответствующий решению х*(b).
Метод проекции градиента для задачи условной оптимизации
Задача v=inf f(x), xU En
Метод xk+1 = PU (xk – αk df(xk))
Метод условного градиента для задачи условной оптимизации
Задача v=inf f(x), xU En
Метод xk+1 = xk + αk (xk′ - xk),
где xk′ - решение вспомогательной задачи
inf (df(xk), xk′ - x), x U.
0< αk <=1, αk = +, lim αk = 0
Метод возможных направлений для задачи условной оптимизации
Задача v=inf f(x), gi(x) ≤ 0, i = 1,…,m
Метод xk+1 = xk + αk e,
где e - решение вспомогательной задачи
min σ,
(df(xk), e) ≤ σ,
(dgi(xk), e) ≤ σ, i I(xk)
|e| ≤ 1
Порядок выполнения лабораторной работы
-
Построить допустимую область задачи и линии уровня.
-
Записать функцию Лагранжа и необходимые условия экстремума, из которых аналитически или используя прикладные пакеты найти условно-стационарные точки.
-
Для каждой точки указать активные и пассивные ограничения. Проверить выполнение достаточных условий экстремума в найденных стационарных точках. Найти глобальный минимум функции. Используя критерий (утверждение 1), проверить, что найденная точка является седловой точкой функции Лагранжа.
-
Решить задачу квадратичного программирования методом седловой точки. Для этого записать систему (14)-(15), найти ее решения, удовлетворяющие условиям (16)-(17).
-
Проверить справедливость оценки (18), решив задачу при положительных и отрицательных малых значениях приращения ∆b.
-
Решить задачу численным методом [8]. Метод условной минимизации выбрать самостоятельно. Сравнить результат с теоретическим решением.
Пример выполнения лабораторной работы
-
Минимизировать нелинейную функцию
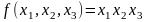 при условиях
при условиях
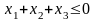 и
и
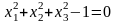 ,
применяя метод функции Лагранжа.
Проверить справедливость оценки
изменения целевой функции (14).
,
применяя метод функции Лагранжа.
Проверить справедливость оценки
изменения целевой функции (14).
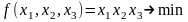
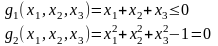
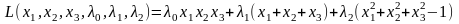
Допустимая
область – часть сферы
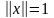 ,
лежащая в подпространстве
,
лежащая в подпространстве
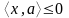 ,
,
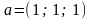 .
.
(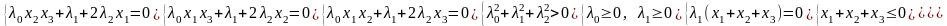 1)
1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
Рассмотрим
случай
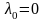 .
.
Если
при этом
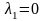 ,
то
,
то
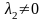 .
.
Из
(1)…(3)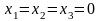 ,
что противоречит (8).
,
что противоречит (8).
Если
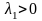 ,
то
,
то
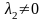 (иначе получаем противоречия в (1)…(3)).
(иначе получаем противоречия в (1)…(3)).
Из
(1)…(3)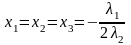 .
Подставим в (6):
.
Подставим в (6):
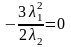 .
Отсюда
.
Отсюда
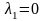 .
Но
.
Но
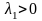 ,
пришли к противоречию.
,
пришли к противоречию.
Рассмотрим
теперь случай
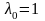 .
.