Добавлен: 19.10.2018
Просмотров: 4024
Скачиваний: 59
СОДЕРЖАНИЕ
1.Исследование функции на безусловный экстремум
2. Численные методы безусловной минимизации
Метод конфигураций (Хука-Дживса)
Метод деформируемого многогранника (Нелдера-Мида)
Метод наискорейшего градиентного спуска
Метод сопряженных направлений (Флетчера – Ривса)
Порядок выполнения лабораторной работы
Пример выполнения лабораторной работы
3. Решение задачи минимизации со смешанными ограничениями
Седловые точки функции Лагранжа
Метод седловой точки в задачах квадратичного программирования
Метод проекции градиента для задачи условной оптимизации
Метод условного градиента для задачи условной оптимизации
Метод возможных направлений для задачи условной оптимизации
Порядок выполнения лабораторной работы
Пример выполнения лабораторной работы
4. Основные понятия линейного программирования
Модель задачи линейного программирования
Свойства задачи линейного программирования
Двойственность в линейном программировании
Построение модели транспортной задачи
Методы нахождения начального плана перевозок.
Задание 2. Числовые характеристики симметричной квадратной матрицы.
Задание 3. Формула Тейлора для функции нескольких переменных
Задание 4. Нахождение локальных экстремумов
Задание 5. Одномерная оптимизация
Задание 6. Многомерная оптимизация по направлению
Задание 7. Методы безусловной оптимизации
Задание 8. Методы условной оптимизации
Задание 9. Задача линейного программирования и симплекс-метод
Задание 10. Транспортная задача
Рис. 3
При классической постановке ТЗ предполагается выполнение условия
Σ Si -Σ Dj =0 (3)
то есть, суммарная мощность всех источников равна суммарной мощности всех стоков (закрытая форма ТЗ). Однако, это условие не является принципиальным, так как при его нарушении можно ввести фиктивный источник, если Σ Si -Σ Dj <0, (или фиктивный сток, если Σ Si -Σ Dj >0), мощность которого равна величине невязки, положив тарифы на перевозку в этот фиктивный узел равными нулю.
Стратегия и методы решения ТЗ
Задача (1),(2) есть задача линейного программирования с ограничениями – равенствами. Число переменных в задаче равно nm. Система ограничений состоит из m+n уравнений, ранг системы равен m+n-1, то есть, любое допустимое базисное решение ТЗ будет содержать m+n-1 базисных переменных.
-
Находится начальный план перевозок.
-
Непосредственно в транспортной таблице производится улучшение начального плана, то есть, последовательный переход от одного плана к другому, связанный с уменьшением суммарной стоимости перевозок.
Методы нахождения начального плана перевозок.
Метод северо-западного угла.
Пользуясь таблицей (1), распределяем груз, начиная с загрузки левой верхней (северо-западной) клетки (1,1), двигаясь из нее по строке вправо или по столбцу вниз. В клетку (1,1) заносим x11=min (S1,D1). При S1<D1 запас первого поставщика будет исчерпан и в дальнейшем первая строка не рассматривается и x1k=0, k=2,...,n. На следующих шагах последовательно распределяются запасы второго, …, n-го поставщиков, пока не будет полностью удовлетворен спрос первого потребителя.
При S1>D1спрос первого потребителя будет полностью удовлетворен и в дальнейшем первый столбец не рассматривается и xk1=0, k=2,...,n.. На следующих шагах последовательно удовлетворяется спрос второго, …, m-го потребителя.
Если S1=D1, то в одну из клеток выбывающих первой строки и первого столбца (лучше в клетку с наименьшим тарифом) заносится так называемый базисный нуль, и xk1=x1k=0, k=2,...,n. В оставшейся таблице распределение ресурсов начинается с северо-западного угла, то есть, с клетки (2,2).
Все нулевые клетки таблицы, кроме (1,1) и клетки с базисным нулем, оставляются пустыми или отмечаются точкой.
Последней будет заполнена клетка (m,n).
Метод северо-западного угла не учитывает величину тарифов, поэтому найденный начальный план перевозок скорей всего будет далек от оптимального.
Метод минимальной стоимости.
Метод аналогичен предыдущему, но на каждом шаге заполнение клеток начинается с клетки, которой соответствует наименьшее значение тарифа cij; при наличии нескольких клеток с одинаковым тарифом заполняется любая из них. В клетку записывается максимально возможное значение поставки. Затем из рассмотрения исключается строка. соответствующая поставщику, запасы которого исчерпаны, либо столбец. соответствующий потребителю, спрос которого удовлетворен полностью. Если в процессе заполнения таблицы одновременно исключаются строка и столбец (это происходит при полном исчерпывании запаса и полном удовлетворении спроса), то в одну из свободных клеток записывается базисный нуль. Клетка с базисным нулем не должна образовывать цикл с ранее занятыми клетками.
Метод потенциалов
Метод обеспечивает переход от одного плана перевозок к другому (от одной матрицы перевозок к другой), соответствующему уменьшению целевой функции.
Введем следующие понятия:
-
Цикл – замкнутая ломаная с вершинами в клетках и звеньями, расположенными вдоль строк и столбцов матрицы перевозок. В каждой вершине встречаются два звена, причем одно из них располагается по строке, а другое – по столбцу. Число вершин цикла четно. Циклом может быть самопересекающаяся ломаная, то точки самопересечения не могут быть вершинами цикла.
-
Означенный цикл – цикл, одной из вершин которого приписан знак »+» и при обходе цикла в каком-либо направлении знаки вершин чередуются.
-
Сдвиг по циклу на величину Q≥0. При этом значения xk1, стоящие в положительных вершинах цикла. увеличиваются на Q, а стоящие в отрицательных вершинах цикла уменьшаются на Q.
Задача, двойственная к ТЗ (1),(2), запишется в виде:
F(u1,...,um,v1,...,vn)= Σ Si ui+Σ Djvj→ max; (4)
ui+ vj≤cij; i=1,...,m, j=1,..., n (5)
где двойственные переменные ui и vj свободные по знаку.
При этом, по теореме о дополняющей нежесткости, для того, чтобы планы пары двойственных задач хij0 и ui0, vj0, удовлетворяющие ограничениям (2),(3) и (4), были оптимальными необходимо и достаточно, чтобы выполнялись условия
хij0(cij- ui0- vj0)=0, i=1,...,m, j=1,..., n (6)
Числа ui и vj, i=1,...,m, j=1,..., n, будем называть потенциалами источников и стоков, соответственно
То есть, для оптимального плана ТЗ необходимо выполнение условий:
-
каждой базисной клетке в транспортной таблице соответствует сумма потенциалов. равная тарифу этой клетки.
-
каждой свободной клетке соответствует сумма потенциалов, не превышающая тарифа этой клетки.
Алгоритм метода потенциалов
-
Найти начальный план перевозок методом северо-западного угла или методом минимальной стоимости.
-
Для каждой из m+n-1 базисных клеток составить уравнение ui+ vj= cij. Решить полученную систему (m+n-1) уравнений с (m+n) неизвестными, для определенности приравняв одну из переменных, например. u1, нулю. Остальные потенциалы при этом определятся однозначно.
-
Для каждой свободной клетки вычислить относительные оценки ∆ij= cij-(ui+ vj).
-
проанализировать относительные оценки:
-
если все относительные оценки неотрицательны, то задача решена и получен оптимальный план перевозки;
-
если среди оценок есть отрицательные, найти наименьшую отрицательную и пометить соответствующую клетку транспортной таблицы знаком «*».
-
Для свободной клетки (i,j) с выбранной оценкой, помеченной «*», построить означенный цикл, взяв эту клетку со знаком “+”. Все остальные вершины цикла должны располагаться в базисных клетках.
-
Выполнить сдвиг по построенному циклу на величину Q, равную наименьшему из тарифов в отрицательных вершинах цикла. Если наименьшее значение достигается в нескольких отрицательных вершинах, то во всех таких вершинах. кроме одной, при сдвиге следует поставить базисный нуль для сохранения числа базисных клеток равным (m+n-1)..Элементы матрицы, не входящие в цикл. остаются без изменений.
-
Перейти на шаг 2.
Замечание 1. В задачах открытого типа (не выполняется условие (3)) предварительно следует ввести фиктивные пункты, а затем решать полученную закрытую ТЗ методом потенциалов.
Замечание 2. В открытых ТЗ может присутствовать дополнительное требование к оптимальному плану: полный вывоз продукции из заданного источника либо полностью удовлетворить потребности заданного стока. В обоих случаях вводятся фиктивные пункты для приведения задачи к закрытому типу и устанавливаются тарифы на перевозку для заданных пунктов, равные М. где М – достаточно большое положительное число.
Замечание 3. Введение дополнительных ограничений может привести к невозможности найти оптимальный план перевозок.
Контрольные задания
Задания 1-6 содержат параметр V, который определяет вариант заданий. Число V является порядковым номером студента в группе.
В заданиях 7-10 вариант определяется также порядковым номером студента в группе по циклу.
Задание 1. Линии уровня
1.1. Приведите определение и свойства линии уровня функции нескольких переменных.
1.2. Укажите связь между линиями уровня и градиентами.
1.3. Постройте линии уровня Uα для функции
y = -V*x1 + 2V*x2
при α=0, α=1, α=2.
1.4. Постройте линию уровня Uα при α=3 для функции
y = x1^2 –V*x1*x2 +2*x2^2 + V*x1.
Вычислите и нарисуйте градиент этой функции в точке (1; 1).
Задание 2. Числовые характеристики симметричной квадратной матрицы.
2.1. Приведите определения и геометрическую интерпретацию числовых характеристик квадратной матрицы:
-
определитель,
-
число обусловленности,
-
собственные числа,
-
собственные векторы,
-
сингулярные числа.
2.2. Найдите гессиан H функции f(x, y) = Vx^2 +4xy+5y^2 в точке (1; 0).
Постройте множество точек, в которое оператор с матрицей H отображает единичную окружность S1 с центром в точке (0; 0). Этот образ является эллипсом. Полуоси являются собственными векторами матрицы H, а длины полуосей – собственными числами i.
2.3. Постройте линию уровня Uα=1 функции f(x, y) в точке (1, 0). Линия уровня также является эллипсом, полуоси которого – собственные векторы, а длин полуосей являются сингулярными числами матрицы и обратно пропорциональны квадратному корню из соответствующего собственного числа, то есть равны 1/i0,5. В некотором смысле, два эллипса из пунктов 5.2 и 5.3 являются ортогональными и взаимно-обратными.
Задание 3. Формула Тейлора для функции нескольких переменных
3.1. Приведите формулу Тейлора для функций одной и нескольких переменных
3.2. Проведите квадратичную аппроксимацию в точке (1; 1) для функции
F(x, y) = (x + y - V) e – (x^2 – xy + y^2)
Задание 4. Нахождение локальных экстремумов
4.1. Используя критерии оптимальности, найдите экстремумы для функции
F(x, y) = (x + y - V) e – (x^2 – xy + y^2)
4.2. Проверьте правильность нахождения точек экстремума двумя свойствами:
-
с помощью графика этой функции,
-
путем случайного перебора точек в малой окрестности точки локального экстремума.
Задание 5. Одномерная оптимизация
Найти точки экстремума функции
F(x) = x6 – Vx5 + Vx3 – 10x2 + x.
Задание 6. Многомерная оптимизация по направлению
Найти точку локального минимума функции
F(x) = x12 +Vx22 + x32 +3x1x2 – Vx1x3 – x2x3 + x1 – Vx2 + x3
Задание 7. Методы безусловной оптимизации
-
Аналитически найти стационарные точки заданной функции, области выпуклости/вогнутости функции. Найти точку глобального минимума. Оценить «овражность» исследуемой функции в окрестности точки минимума.
-
Построить график функции, используя средства EXCEL или MATLAB.
-
Решить задачу минимизации численным методом из нескольких начальных точек. Сделать вывод об эффективности выбранного метода.
-
При выполнении задания на языке СИ написать классы для работы с векторами и матрицами.
Задание выбирать в соответствии с порядковым номером фамилии студента в списке группы.
-
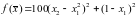 ,
метод Хука-Дживса.
,
метод Хука-Дживса. -
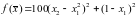 ,
метод наискорейшего спуска.
,
метод наискорейшего спуска. -
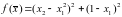 ,
метод Хука-Дживса.
,
метод Хука-Дживса. -
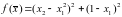 ,
метод сопряженных
направлений.
,
метод сопряженных
направлений. -
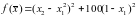 ,
метод Нелдера-Мида.
,
метод Нелдера-Мида. -
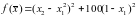 ,
метод Ньютона.
,
метод Ньютона. -
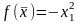 exp[1-
exp[1-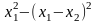 ],
метод
Нелдера-Мида.
],
метод
Нелдера-Мида. -
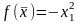 exp[1-
exp[1-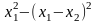 ],
метод наискорейшего спуска.
],
метод наискорейшего спуска. -
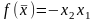 exp[1-
exp[1-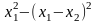 ],
метод
сопряженных
направлений.
],
метод
сопряженных
направлений. -
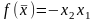 exp[1-
exp[1-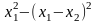 ],
метод Хука-Дживса.
],
метод Хука-Дживса. -
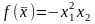 exp[1-
exp[1-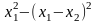 ],
метод
Ньютона.
],
метод
Ньютона. -
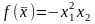 exp[1-
exp[1-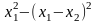 ],
метод дробления
шага.
],
метод дробления
шага. -
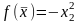 exp[1-
exp[1-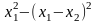 ],
метод
наискорейшего спуска.
],
метод
наискорейшего спуска. -
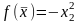 exp[1-
exp[1-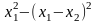 ],
метод Нелдера-Мида.
],
метод Нелдера-Мида. -
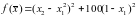 ,
метод дробления
шага.
,
метод дробления
шага. -
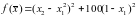 ,
метод Ньютона.
,
метод Ньютона.
-
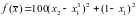 ,
метод Нелдера-Мида.
,
метод Нелдера-Мида. -
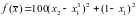 ,
метод сопряженных
направлений.
,
метод сопряженных
направлений. -
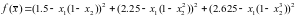 ,
метод наискорейшего спуска.
,
метод наискорейшего спуска. -
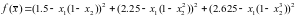 ,
метод Ньютона.
,
метод Ньютона. -
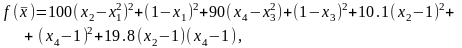 метод
Ньютона.
метод
Ньютона. -
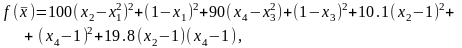
метод дробления шага.
-
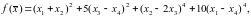 метод
наискорейшего спуска
метод
наискорейшего спуска -
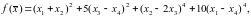 метод
Нелдера-Мида.
метод
Нелдера-Мида. -
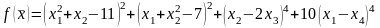 ,
метод Ньютона.
,
метод Ньютона. -
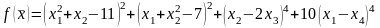 ,
метод наискорейшего спуска
,
метод наискорейшего спуска -
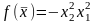 exp[1-
exp[1-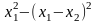 ],
метод
дробления шага.
],
метод
дробления шага. -
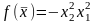 exp[1-
exp[1-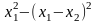 ],
метод Нелдера-Мида.
],
метод Нелдера-Мида. -
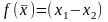 exp[1-
exp[1-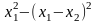 ],
метод
сопряженных
направлений.
],
метод
сопряженных
направлений. -
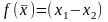 exp[1-
exp[1-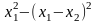 ],
метод
Ньютона.
],
метод
Ньютона.
Контрольные вопросы
Объяснить алгоритмы следующих методов
-
Метод конфигураций (Хука-Дживса).
-
Метод деформируемого многогранника (Нелдера Мида).
-
Метод наискорейшего спуска.
-
Метод сопряженных направлений и его модификации.
-
Метод Ньютона и его модификации.
-
Метод дробления шага.
Задание 8. Методы условной оптимизации
-
Решить задачу минимизации функции методом множителей Лагранжа.
-
Решить ЗНП методом седловой точки. Промежуточную задачу решения СЛАУ решить, используя EXCEL.
-
Решить задачу численным методом [8]. Метод условной минимизации выбрать самостоятельно (см. 1.4.-1.6). Сравнить результат с теоретическим решением.
Задания выбирать в соответствии с порядковым номером студента в журнале.
1.
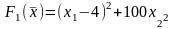 ,
,
2.
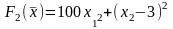 .
.
3.
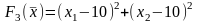
4.
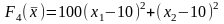
5.
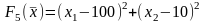
6.
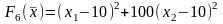
7.
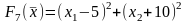
8.
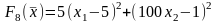
Ограничения (для всех вариантов):
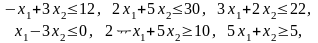
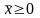 .
.
Контрольные вопросы
-
Активные и пассивные ограничения. Регулярная задача.
-
Теорема Куна-Такера.
-
Достаточные условия минимума в задачах математического программирования.
-
Седловая точка.
-
Метод седловой точки для задачи квадратичного программирования.
Задание 9. Задача линейного программирования и симплекс-метод
Вариант 1. Для изготовления четырёх видов продукции (А, Б, В и Г) используется три вида сырья (I, II и III). Ресурсы сырья, нормы его расхода на единицу продукции и получаемая прибыль от единицы продукции заданы в следующей таблице:
|
Сырьё |
Нормы расхода |
Ресурсы Б |
||||
|
А |
Б |
В |
А |
|||
|
I |
2 |
1 |
I |
2 |
1 |
|
|
II |
1 |
5 |
II |
1 |
5 |
|
|
III |
3 |
0 |
III |
3 |
0 |
|
|
Прибыль |
7,5 |
3 |
Прибыль |
7,5 |
3 |
|
Определить оптимальный план выпуска продукции из условия максимизации прибыли.
Вариант 2. Четыре различных предприятия могут выпускать любой из четырёх видов продукции. Производственные мощности предприятий позволяют обеспечить выпуск продукции каждого вида 50, 70, 100 и 30 тыс. шт., а плановое задание составляет соответственно 30, 80, 20 и 100 тыс. шт. Матрица
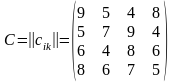
характеризует себестоимость единицы k-го вида продукции при производстве его на i-ом предприятии.
Найти оптимальное распределение планового задания между предприятиями.
Вариант 3. Для контроля за работой космической ракеты используются четыре вида датчиков (А, Б, В и Г), которые помещены на ракете и результаты измерений которых регистрируются тремя типами наземных регистраторов (I, II, и III). Каждый датчик определяет одну из характеристик (температуру, давление и т.д.) и передаёт результаты по отдельному каналу связи на любой регистратор. В следующей таблице указаны численности датчиков и регистраторов, а также время, затрачиваемое на включение соответствующего канала связи
|
|
|
Датчики |
||||
|
А |
Б |
В |
Г |
|||
|
Число |
20 |
40 |
50 |
60 |
||
|
Регистраторы |
Тип I |
70 |
2 |
1 |
5 |
3 |
|
Тип II |
90 |
3 |
2 |
3 |
4 |
|
|
Тип II |
60 |
3 |
4 |
1 |
2 |
|
Определить оптимальное закрепление датчиков к регистраторам, при котором достигается минимум суммарных затрат на переключение каналов.
Вариант 4. Поверхность ювелирного изделия составляет 400 см2. Основной узор занимает 100 см2, а площадь не украшенных полей – тоже 100 см2. На оставшуюся часть поверхности необходимо нанести инкрустацию топазами, сапфирами, золотой протяжкой и серебряной чеканкой. При этом топазы должны занимать площадь не менее 80 см2 и не более 100 см2. Сапфиры должны по эстетическим соображениям занимать площадь не более 25% от площади, занимаемой топазами, но и не менее 10 см2. Площадь золотой инкрустации не должна быть более 10 см2, а площадь серебряной чеканки не менее площади, занимаемой сапфирами и не менее удвоенной площади золотой чеканки, но в то же время и не более 50 см2.
Необходимо определить минимальное время, необходимое для инкрустации изделия, если известны затраты времени на каждую операцию: на установку топазов – 20 мин/см2, установку сапфиров – 25 мин/см2, на покрытие золотом – 120 мин/см2, на покрытие серебром – 100 мин/ см2.