Файл: 1. Лекции Паскаль (Часть 1).doc

Содержание отчета:

1. Постановка задачи.

2. Текст программы.

3. Таблица результатов.

Образец выполнения задания.

Лабораторная работа № 3, вариант № 8.

Построение таблиц функций.

Постановка задачи.

Составить программу вычисления значений функции arctg(x) на отрезке [A, B] в точках Xi = A + iH, где H = (B - A)/M, M — заданное целое число. Значение шага Н должно вычисляться один раз.

При A=2, B=7, M=15.

Текст программы.

program lab3{ вариант № 8};

var h,r:real;

n:integer;

begin

h:=(7-2)/15;

r:=2;

for n:=1 to 16 do

begin

writeln('arctg(',r:5:4,')=',(arctan(r)):5:4);

r:=r+h;

end;

end.

Таблица результатов

Варианты заданий

Лабораторная работа № 4.

Организация циклов в программе.

Рекуррентной называется формула, связывающая значения р+1 соседних членов uk, uk-1, …, uk-p (k>=p+1) некоторой последовательности {un}(n=1, 2, …): uk=F(k, uk-1, …, uk-p). Рекуррентная формула позволяет шаг за шагом определить любой член последовательности, если известны р первых её членов u1, u2, …, up, где р называют порядком формулы. Рассмотрим пример.

Рассмотрим задачу нахождения n-го члена рекуррентной последовательности на примере чисел Фибоначчи. Каждое число Фибоначчи равно сумме двух предыдущих. В частности:

U3 = u2+u1 = 1+1 = 2;

U4 = u3+u2 = 1+2 = 3 и т.д.

Отсюда следует, что для получения очередного числа достаточно хранить два предыдущих. Таким образом, в программе постоянно используются три соседних числа Фибоначчи. Для их хранения достаточно ввести три переменных: А хранит uk, B хранит uk-1, С хранит uk-2. Для вычисления следующего числа Фибоначчи необходимо провести сдвиг, т.е. переписать содержимое В в С, а содержимое А в В. Исходя из этого, получим фрагмент

{фрагмент}

c:=1;{значение первого числа известно}

b;=1;{значение второго числа тоже известно}

k:=3;{начинаем вычисление с третьего числа}

while k<=n do {цикл, пока не найдено n-е число}

begin

a:=b+c;{вычисляем следующее число как сумму двух предыдущих}

c:=b;{сдвигаем b в c для нахождения следующего числа}

b:=a;{сдвигаем a в b для нахождения следующего числа}

k:=k+1;{увеличиваем счетчик найденных чисел}

end;

write(a);{выводим найденное число}

Цель задания:

1. Получение навыков в выборе и использовании

операторов цикла.

2. Знакомство с итерационными процессами.

Постановка задачи:

Используя оператор цикла, найти сумму элементов, указанных в конкретном варианте. Результат напечатать, снабдив соответствующим заголовком.

Содержание отчета:

1. Постановка задачи.

2. Текст программы.

3. Результат решения конкретного варианта.

Методические указания:

При определении суммы членов ряда следует использовать рекуррентную формулу для получения следующего члена ряда.

Факториалом целого числа называют произведение

1*2*3*…*n = n!

n! = n*(n-1)

Например, требуется найти сумму ряда с точностью =10^-4, общий член которого .

Для получения рекуррентной формулы вычислим отношение:

,

откуда:

.

При составлении программы считать, что точность достигнута, если а_n <

Образец выполнения задания.

Лабораторная работа № 4, вариант № 8.

Организация циклов в программе.

Постановка задачи:

Используя оператор цикла, найти сумму ряда с точностью =10^-4, общий член

которого . Результат напечатать.

При определении суммы членов ряда следует использовать рекуррентную формулу, в нашем случае рекуррентная формула имеет вид: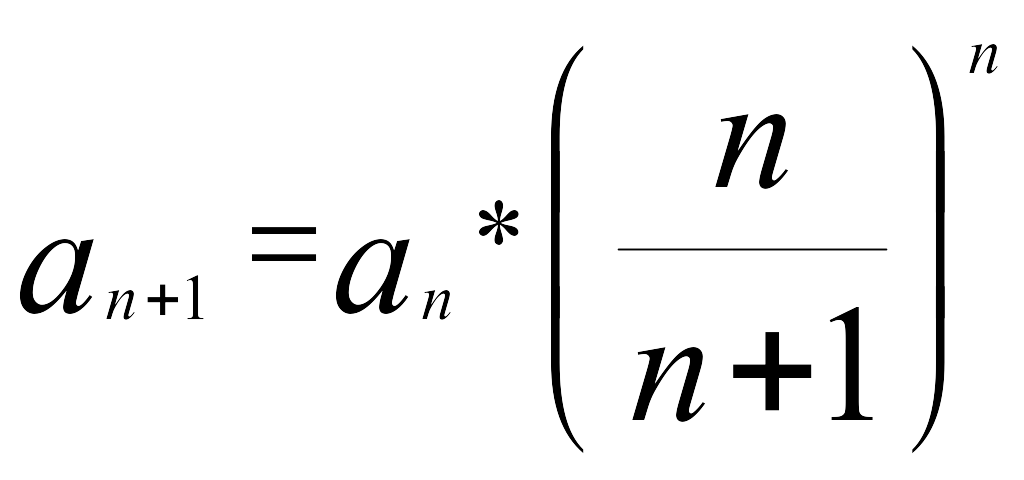

При составлении программы считать, что точность достигнута, если а_n <10^-4

Текст программы:

program lab4{вариант № 11};

var sum,an:real;

n:integer;

begin

clrscr;

sum:=0;

an:=1;

n:=1;

while an>0.0001 do

begin

sum:=sum+an;

n:=n+1;

an:=an*(exp(n*(ln(n/(n+1)))));

end;

writeln('Сумма ',n,' элементов равна =',sum:7:6);

end.

Результат решения конкретного варианта:

Варианты заданий

1) Найти сумму целых положительных чисел, кратных 3 и

меньших 200.

2) Найти сумму целых положительных четных чисел,

меньших 100.

3) Найти сумму целых положительных нечетных чисел,

меньших 200.

4) Найти сумму целых положительных чисел, больших 20,

меньших 100 и кратных 3.

5) Найти сумму ряда с точностью =10^-4, общий член

которого

6) Найти сумму ряда с точностью =10^-4, общий член

которого

7) Найти сумму ряда с точностью =10^-4, общий член

которого

8) Найти сумму ряда с точностью =10^-4, общий член

которого

9) Найти сумму ряда с точностью =10^-4, общий член

которого

10) Найти сумму ряда с точностью =10^-4, общий член

которого

11) Найти сумму ряда с точностью =10^-4, общий член

которого

12) Найти сумму ряда с точностью =10^-4, общий член

которого

13) Найти сумму ряда с точностью =10^-4, общий член

которого

14) Найти сумму ряда с точностью =10^-4, общий член

которого

15) Найти сумму ряда с точностью =10^-4, общий член

которого

16) Найти сумму ряда с точностью =10^-4, общий член

которого

17) Найти сумму ряда с точностью =10^-4, общий член

которого

18) Найти сумму ряда с точностью =10^-4, общий член

которого

19) Найти сумму ряда с точностью =10^-4, общий член

которого

20) Найти сумму 13 членов ряда, в котором

21) Найти сумму 15 членов ряда, в котором

22) Найти сумму 10 членов ряда, в котором

23) Найти сумму 9 членов ряда, в котором

24) Найти сумму 7 членов ряда, в котором

3.Численные методы.

Довольно часто на практике приходится решать уравнения вида:

F(x) = 0, (1)

где функция F(x) определена и непрерывна на некотором конечном или бесконечном интервале  < x < .

Всякое значение такое, что F(x)  0, называется корнем уравнения, а нахождение этого значения и есть решение уравнения.

На практике в большинстве случаев найти точное решение возникшей математической задачи не удается. Поэтому важное значение приобрели численные методы, позволяющие найти приближенное значение корня. Под численными методами подразумеваются методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами, т.е. к тем действиям, которые выполняет ЭВМ. [5]

Существует множество численных методов. Рассмотрим только три из них:

1. метод итераций;

2. метод Ньютона;

3. метод половинного деления.

3.1.Метод итераций

Этот метод заключается в замене уравнения (1) эквивалентным ему уравнением вида (2)

После этого строится итерационный процесс

(3)

При некотором заданном значении . Для приведения выражения (1) к требуемому виду (2) можно воспользоваться простейшим приёмом

,

.

Если в выражении (2) положить , можно получить стандартный вид итерационного процесса для поиска корней нелинейного уравнения:

Иначе можно получить уравнение (2) следующим способом: левую и правую часть уравнения (1) умножить на произвольную константу  и прибавить к левой и правой части х, т.е. получаем уравнение вида:

х = х + F(x), (4)

где f(x) = х + F(x).

На заданном отрезке [a; b] выберем точку х₀ – нулевое приближение – и найдем:

х₁ = f(x₀),

потом найдем:

х₂ = f(x₁),

и т.д.

Таким образом, процесс нахождения корня уравнения сводится к последовательному вычислению чисел:

х_n = f(x_n-1) n = 1,2,3..... .

Этот процесс называется методом итераций.

Если на отрезке [a; b] выполнено условие:

,

то процесс итераций сходится, т.е.

lim x_n = x.

n  

Процесс итераций продолжается до тех пор, пока

x_n - x_n-1 ,

где  – заданная абсолютная погрешность корня х. При этом будет выполняться:

x - x_n .

Блок-схема метода итераций.

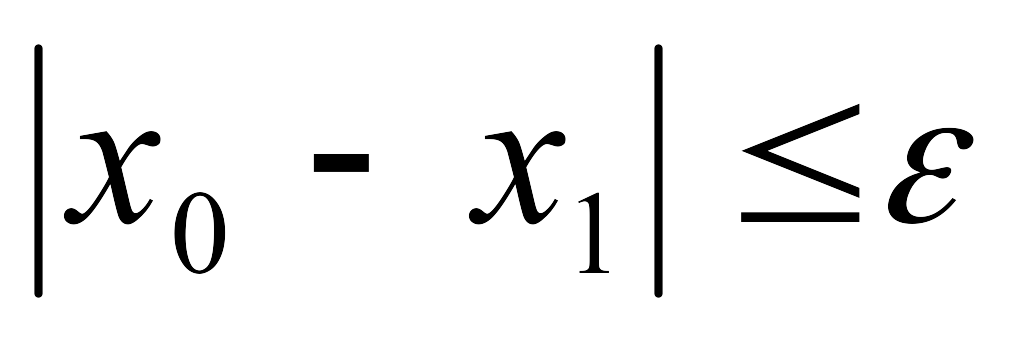true false

3.2.Метод Ньютона

Для поиска корней уравнения (1) в окрестности решения выберем точку и разложим функцию в ряд Тейлора возле этой точки:

Отсюда следует приближённое равенство

Которое с учётом

Позволяет получить выражение

Приводящее к итерационному процессу следующего вида:

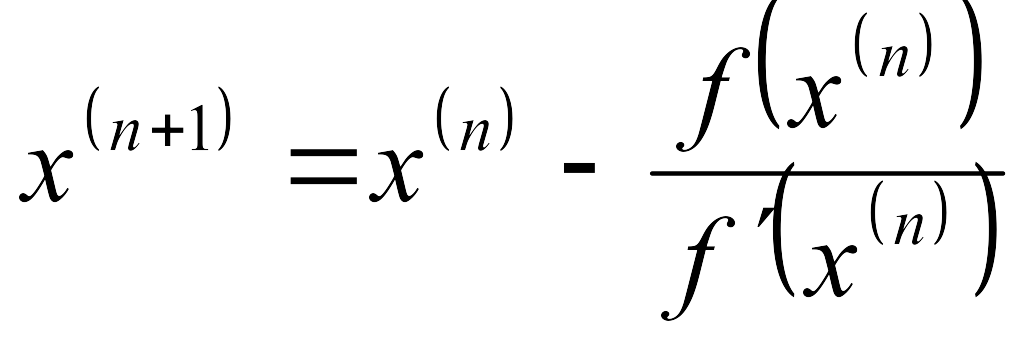
Выберем на отрезке[a; b] произвольную точку х₀ – нулевое приближение. Затем найдем:

x₁ = x₀ - ,

потом x₂ = x₁ - .

Таким образом, процесс нахождения корня уравнения сводится к вычислению чисел x_n по формуле:

x_n = x_n-1 - n = 1,2,3...... .

Процесс вычисления продолжается до тех пор, пока не будет выполнено условие:

x_n - x_n-1 < .

Очевидно, что метод Ньютона можно рассматривать как вариант метода простых итераций, при условии .

Геометрическая иллюстрация итерационного процесса метода Ньютона приведена на рисунке, из которого понятно, что каждое следующее приближение может быть определено из геометрических построений:

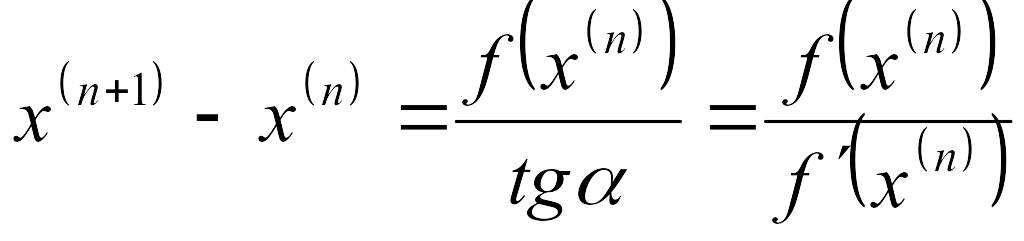
Этот процесс называется методом Ньютона.

Блок-схема метода Ньютона.

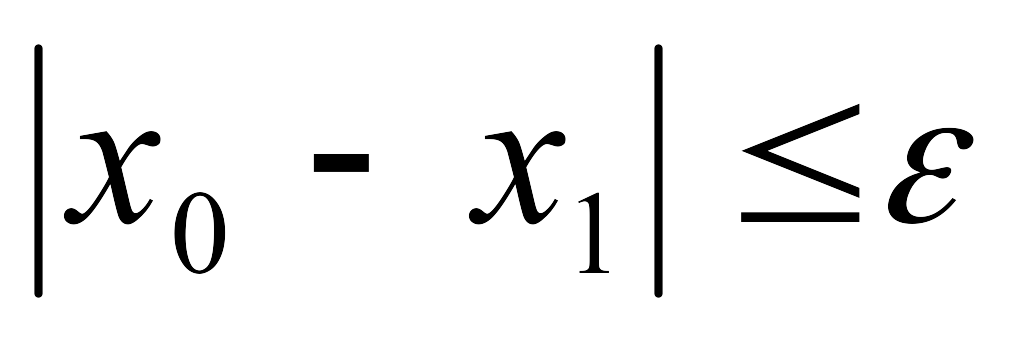true false

Геометрический смысл процедуры Ньютона

Пример. Требуется определить корни уравнения .

Согласно рассмотренному методу Ньютона строится итерационная процедура

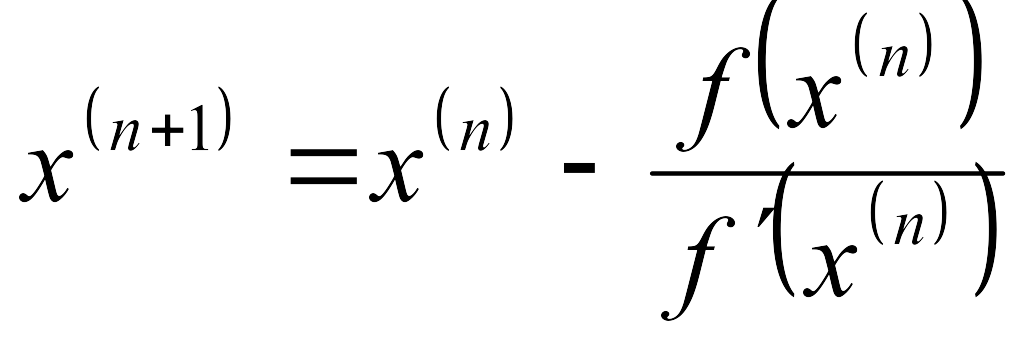
Поскольку

Таким образом, применение процедуры метода Ньютона к заданному уравнению приводит к вычислительному процессу

Для а=2 ‘точное’ решение .Результаты расчётов приведены в таблице 3.2.

Последовательность получения приближённого решения уравнения методом Ньютона.

3.3. Метод половинного деления.

Пусть уравнение F(x) = 0 имеет один корень на отрезке [a;b]. Функция F(x) непрерывна на отрезке [a; b].

Метод половинного деления заключается в следующем:

Сначала выбираем начальное приближение, деля отрезок пополам, т.е. х₀ = (a+b)/2.

Если F(x)=0, то x₀ является корнем уравнения. Если F(x) 0, то выбираем тот из отрезков, на концах которого функция имеет противоположные знаки. Полученный отрезок снова делим пополам и выполняем действия сначала и т.д.

Процесс деления отрезка продолжаем до тех пор, пока длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше заданного числа .

Блок-схема метода половинного деления.

true false

false true

Теорема математического анализа метода половинного деления.

Согласно тому что функция, непрерывна в замкнутом интервале и принимающая на концах этого интервала значения разных знаков, хотя бы один раз обращается в нудь внутри интервала.

Пусть функция непрерывна на отрезке [,]. Процедура метода заключается в последовательном сокращении длинны отрезка для локализации корня уравнения. Первоначально проверяются значения заданной функции на концах отрезка.

В случае, если

,

Один из концов отрезка является корнем уравнения.

Пусть на концах отрезка значения функции имеют разные знаки, то есть имеет место соотношение ,

Вычисляется значение аргумента в середине отрезка,, и вычисляется значение

функции в этой точке.

Далее сравниваются знаки функций в точке например, в левой точке отрезка.

Если имеет место соотношение (рис.3.1), то корень следует искать на отрезке. В противном случае-корень разыскивается на отрезке, в результате выполненной операции исходный отрезок сократился вдвое.

Схема метода половинного деления.

Далее, в зависимости от ситуации, отрезок вновь делится пополам,

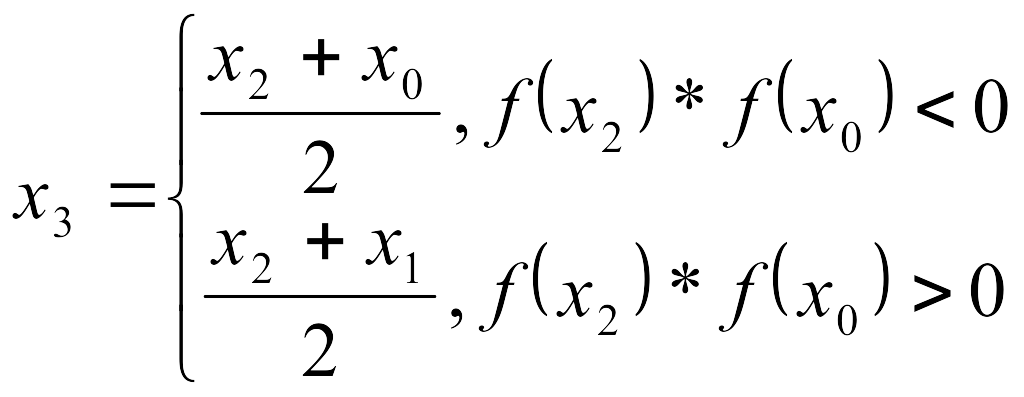
И так далее.

Для прекращения вычислительной процедуры применяют различные критерии:

-если функция достаточно ‘пологая’, имеет смысл использовать условие (рис. а).

-если функция ‘круто’ меняет своё значение, целесообразно применять условие(рис. b).

b

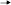
Частные случаи поиска корня нелинейного уравнения

В случае, если заранее неизвестен характер ‘поведения’ функции, имеет смысл использовать одновременно оба условия для прекращения итерационного процесса.

Лабораторная работа № 5

Решение нелинейных уравнений.

Цель работы:

1. Получение практических навыков в организации итерационных циклов.

2. Знакомство с методами решения алгебраических и трансцендентных уравнений.

3. Получение навыков составления блок-схемы алгоритма и определения данных.