Добавлен: 15.11.2018
Просмотров: 2701
Скачиваний: 7
11
№
задан.
Источник
сообщений
Передающее устройство
Канал
связи
Приемное
устройство
ЦАП
Функция
P
g
,
В
2
β, mс
-1
α
Способ
передачи
Частота, МГц
N
0
,
мВт⋅с
h
2
Способ
приёма
δ
2доп
корреляции сообщения
f
0
(f
2
)
f
1
B
c
(
τ)
21
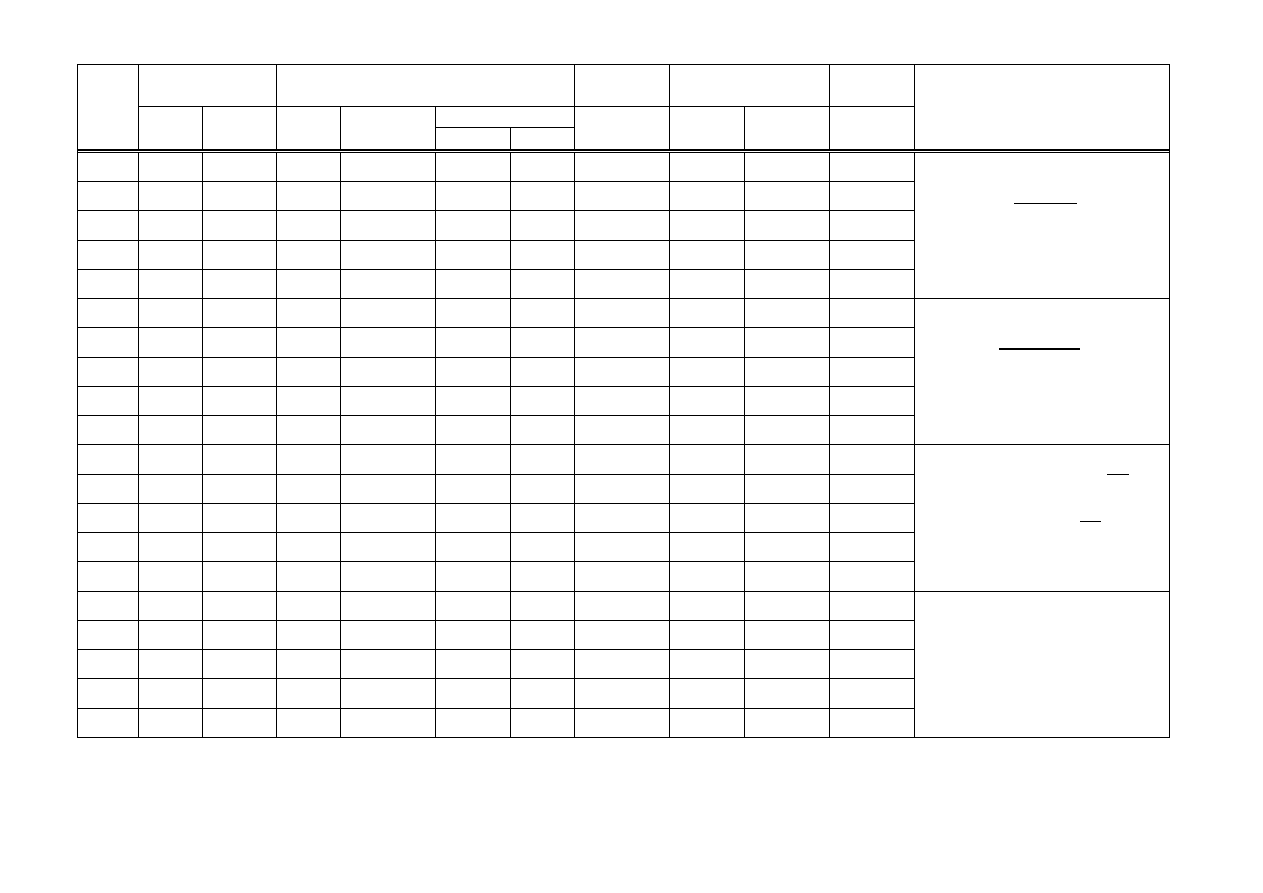
4,4
7
1,5
ОФМ
40
0,0022
6,1
СФ
0,13
P
g
sin(2πβτ)
(2πβτ)
2
2
,
|τ|
≤ 1/2β;
f
g
=
β
22
4,6
8
2,0
АМ
41
0,0008
18,0
НО
0,15
23
4,8
9
2,5
ЧМ
42
43,5
0,0017
12,0
КО
0,17
24
5,0
10
3,0
ОФМ
43
0,0023
6,4
СП
0,19
25
3,8
13
3,5
АМ
44
0,0009
18,5
КО
0,1
26
3,3
14
3,5
ЧМ
45
46,5
0,0018
12,5
НО
0,12
P
g
cos(2πβτ)
1−(4βτ)
2
,
−∞ < τ < ∞;
f
g
= 4β.
27
2,8
15
3,0
ОФМ
46
0,0024
6,7
СФ
0,14
28
2,3
16
2,5
АМ
47
0,0004
19,0
НО
0,16
29
1,8
17
2,0
ЧМ
48
49,5
0,0019
13,0
КО
0,18
30
1,3
18
1,5
ОФМ
49
0,0025
7,0
СП
0,2
31
3,6
7
1,5
АМ
50
0,0005
19,5
КО
0,09
⎩
⎨
⎧P
g
????????????????????????(2????????????????????????), |????????| ≤
1
4???????? ;
0, |????????| >
1
4???????? ;
f
g
= 3β.
32
3,1
8
2,0
ЧМ
51
52,5
0,002
13,5
НО
0,11
33
2,6
9
2,5
ОФМ
52
0,0026
7,3
СФ
0,13
34
2,1
10
3,0
АМ
53
0,0006
20,0
НО
0,15
35
1,6
11
3,5
ЧМ
54
55,5
0,0021
14,0
КО
0,17
36
1,1
12
3,5
ОФМ
55
0,0027
7,6
СП
0,19
P
g
(1 − β|τ|)exp(−βτ);
f
g
= 2β.
37
1,2
6
3,0
АМ
56
0,0009
8,0
НО
0,12
38
1,5
9
2,5
ЧМ
57
58,5
0,0011
10,0
КО
0,13
39
1,7
12
2,0
ОФМ
58
0,0015
12,0
СФ
0,14
40
1,9
15
1,5
АМ
59
0,0018
15,0
КО
0,15

12
–
распределение вероятностей р
j
, j = {
1, L + 1
����������}, и интегральное распреде-
ление вероятностей F
j
, j = {
1, L + 1
����������} квантованной последовательности {v
k
j
};
–
энтропию Н
y
, производительность R
y
и избыточность ζ квантованной по-
следовательности. В системе используется квантование с равномерным шагом.
2.2.3
Закодировать L-ичную последовательность {v
k
j
}
на выходе АЦП
двоичным безизбыточным блочным кодом {b
k
µ
},
выписать все кодовые комби-
нации и построить таблицу кодовых расстояний {d
lm
}, l,m
∈ {1, L + 1
����������} кода.
Рассчитать априорные вероятности р(0) и p(1) передачи нулевого и еди-
ничного символов соответственно по двоичному ДКС, а также ширину спектра
цифрового сигнала Δf
ц
.
2.2.4
Изобразить спектр сигнала с дискретной модуляцией и рассчитать
его ширину Δf
s
.
2.2.5
Рассчитать:
►
мощность Р
s
,
приходящуюся в среднем на один двоичный символ (бит);
►
амплитуду U
m
сигнала дискретной модуляции, необходимую для обес-
печения требуемого соотношения сигнал/шум h
2
на входе приемника;
►
пропускную способность С гауссовского НКС.
2.2.6
Изобразить схему приемника сигнала дискретной модуляции (вы-
полняется при построении структурной схемы всей системы).
2.2.7
Рассчитать:
–
среднюю вероятность ошибки р
ош
и скорость передачи информации R
2
по двоичному симметричному ДКС;
–
показатель эффективности передачи сигнала дискретной модуляции Э
по НКС;
–
скорость передачи информации R
L
по L-ичному ДКС и относительную
потерю в скорости передачи информации;
2.2.8
Рассчитать среднее квадратическое значение шума передачи ξ
2п
и
относительную суммарную СКО ξ
2Σ
восстановления непрерывного сообщения.
Указать пути уменьшения величины ξ
2Σ
,
если окажется, что ξ
2Σ
>
δ
2доп
.
2.3.
Структурная схема системы передачи информации
В цифровых и дискретных системах связи возникает необходимость пе-
редачи непрерывного сообщения по дискретному (цифровому) каналу связи.
Эта проблема решается при использовании смешанной системы связи. Одной
из возможных является система передачи непрерывного сообщения с использо-
ванием импульсно-кодовой модуляции (ИКМ)
. Структурная схема такой си-
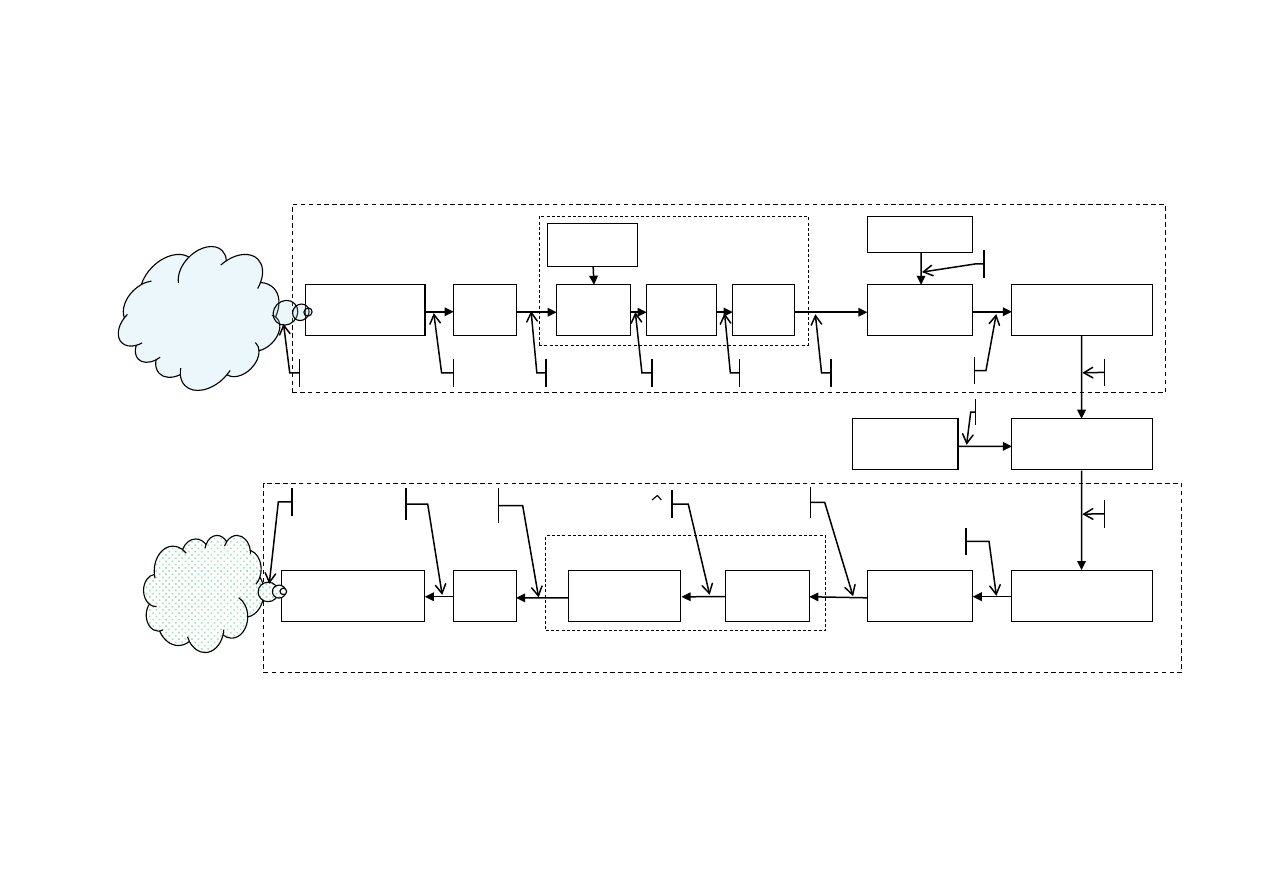
стемы приведена на рис. 1.
1
Выполняется по отдельному заданию преподавателя.
2
Общепринятый термин процедуры преобразования непрерывного (аналогового) сигнала в цифровую форму.
Фактически не содержит несущего колебания и модуляции, как процесса изменения его параметра в соответ-
ствии с модулирующим сигналом.
13
Рис. 1. Структурная схема системы передачи информации
ПРУ
ПДУ
Входное уст-во
ПРУ
Ц А П
Выходной
преобразователь
ФНЧ
Детектор
(РУ)
Интерполятор
Декодер
Получатель
c(t)
g(t)
x(t)
x(
k·Δt)
v
k
j
b
k
µ
s(t, b
k
µ
)
S(t)
n(t)
z(t)
ŝ(t, b
k
µ
)
b�
k
µ
v
k
j
x�(t)
g�(t)
ĉ(t)
Генератор
u
н
(t)
Источник
помех
Линия
связи
А Ц П
Первичн. преоб-
разователь
ФНЧ
Дискрети-
затор
Квантова-
тель
Кодер
Источник
сообщений
Модулятор
Выходное уст-во
ПДУ
Генератор
δ(t)

14
Она состоит из источника сообщений (ИС), аналого-цифрового преобра-
зователя (АЦП), двоичного дискретного канала связи (ДКС), составной частью
которого является непрерывный канал линии связи (НКС), цифро-аналогового
преобразователя (ЦАП) и выходного преобразователя сигнала в сообщение.
Источник сообщений – это некоторый объект или система, информацию о
состоянии или поведении которых необходимо передать получателю, находяще-
муся на удалении. Причем объектом или системой может быть человек, ЭВМ, по-
езд, состояние стрелок и светофоров на станции и т. п. Передаваемые сообщения,
до их поступления, получателю неизвестны. Поэтому количественную меру ин-
формации, передаваемой по системе связи, в теории электросвязи выражают через
статистические (вероятностные) характеристики сообщений (сигналов).
Сообщение – это физическая форма представления информации. Пер-
вичный преобразователь представляет сообщение в виде первичного электри-
ческого сигнала g(t) – изменяющегося во времени напряжения или тока, отоб-
ражающего передаваемую информацию. Например: в телефонии – это измене-
ние выходного напряжения или тока микрофона под воздействием звукового
давления от речи человека; в телевидении – это изменение напряжения или то-
ка на выходе видеокамеры в соответствии с изменением яркости и цветности
отображаемого объекта; в телеграфии – токовые или бестоковые посылки кодо-
вых комбинаций на выходе телеграфного аппарата и т. п.
В ПДУ первичный сигнал пропускается через ФНЧ с целью ограничения
его спектра некоторой верхней частотой f
ср
. Это необходимо для уменьшения
погрешности последующего преобразования дискретизатором АЦП выходного
сигнала ФНЧ х(t) в последовательность отсчетов x
k
≡ x(k·Δt). Отметим, что
фильтрация связана с внесением своей, но меньшей, погрешности ξ
ф
(t),
соот-
ветствующей той части сообщения, которая подавляется в ФНЧ. Отсчеты {х
k
}
квантуются по уровню в квантователе АЦП. Процесс квантования связан с не-
линейным преобразованием непрерывнозначных отсчетов {х
k
}
в дискретно-
значные {v
k
j
}, j
∈ {1, L + 1
����������}, что также вносит погрешность, называемую по-
грешностью (шумом) квантования ξ
q
(t).
Значения уровней квантования {v
k
j
}
да-
лее кодируются двоичным безизбыточным кодом – комбинациями {b
k
μ
}.
Последовательность кодовых комбинаций {b
k
µ
} образует сигнал, назы-
ваемый сигналом ИКМ, который подается на модулятор – устройство, предна-
значенное для согласования спектра сигнала, несущего сообщение, с частотной
характеристикой используемой линии связи.
Модулятор формирует линейный сигнал s(t, b
k
µ
), который представляет
собой электрическое или электромагнитное колебание, способное распростра-
няться по линии связи и однозначно связанное с передаваемым сообщением (в
данном случае с цифровым сигналом). При использовании гармонической не-
сущей u
н
(t) = U
0
соs(2πf
н
+
φ
0
) различают сигналы с амплитудной (АМ), частот-
ной (ЧМ) и фазовой (ФМ) модуляцией или манипуляцией.
Для подавления внеполосных излучений в одноканальной системе связи
или при организации многоканальной связи, а также для установления требуе-

15
мого отношения С/Ш на входе приемника, сигнал s(t, b
k
µ
)
фильтруется и усили-
вается в выходном каскаде ПДУ, формируя сигнал S(t).
С выхода ПДУ S(t) поступает в линию связи, где на него воздействует
помеха n(t). На вход ПРУ поступает сумма z(t) = χS(t) + n(t) переданного сигна-
ла и помехи. Коэффициент χ < 1 учитывает процесс ослабления сигнала S(t) при
распространении по линии связи.
Во входном каскаде ПРУ z(t) усиливается, фильтруется и подается на
детектор. При демодуляции из принятого сигнала s�(t, b
k
µ
) выделяется функция
изменения информационного параметра, который в данной системе пропорци-
онален цифровому сигналу. При этом для выделения переданных двоичных
символов к выходу демодулятора подключено решающее устройство (РУ). При
передаче двоичных сигналов с алфавитом B∈{1, 0} по ДКС, наличие помех в
НКС приводит к неправильным решениям (ошибкам) РУ, что вызывает некото-
рое отличие принятых b�
k
µ
кодовых комбинаций от переданных b
k
µ
.
Для восстановления переданного непрерывного сигнала сообщения – полу-
чения его оценки ĝ(t), принятые кодовые комбинации подвергаются декодированию,
интерполяции и низкочастотной фильтрации. При этом в декодере по двоичным ко-
довым комбинациям восстанавливаются L-ичные уровни {v�
k
j
},
j ∈ {1, L + 1
����������}.
Наличие ошибок в двоичном ДКС приводит к ошибкам передачи в L-
ичном ДКС и к возникновению шума передачи ξ
n
(t
). Совокупное действие по-
грешности фильтрации, шумов квантования и передачи приводит к неодно-
значности между переданными и принятыми сигналами сообщений ĝ(t) ≠ g(t).
Работа системы передачи информации считается удовлетворительной,
если суммарная относительная СКО восстановления первичного сигнала не
превосходит допустимую, т.е. δ
2Σ
= ∫ [g(t) − g�(t)]
2
dt
Т
с
0
≤ δ
2доп
,
где Т
с
–
длитель-
ность первичного сигнала g(t).
2.4.
Анализ статистических характеристик и параметров передан-
ного сообщения
По условию задания исходный первичный сигнал непрерывного сооб-
щения g(t) представляет собой стационарный гауссовский случайный процесс с
нулевым математическим ожиданием g
ср
= М{g(t)} = 0, где М{·} – операция
статистического усреднения по множеству реализаций. Мощность (дисперсия)
процесса P
g
=
σ
g
2
= M{[g(t) – g
ср
]
2
}
и функция корреляции В
c
(
τ) = М{[g(t) –
g
ср
]·[g(t+
τ) – g
ср
]}
первичного сигнала заданы в табл. 1.
Стационарный гауссовский (нормальный) случайный процесс с нулевым
средним значением в любой момент времени характеризуется одномерной ФПВ
следующего вида:
w
g
(u) =
1
σ
g
√2π
exp �−
u
2
2σ
g
2
�, u∈[-∞; ∞].
Стационарный случайный процесс во временной области характеризует-
ся функцией корреляции В
c
(
τ) и в частотной области – спектром плотности
(1)