Добавлен: 15.11.2018
Просмотров: 2707
Скачиваний: 7

16
мощности или энергетическим спектром G
g
(
ω), где ω = 2πf. Эти характеристики
связаны между собой парой преобразований Винера-Хинчина:
G
g
(
ω) = ∫ B
c
(τ)e
−jωτ
dτ
∞
−∞
,
В
c
(
τ) =
1
2π
∫ G
g
(ω)e
jωτ
dω
∞
−∞
.
Учитывая, что для стационарного случайного процесса обе эти функции
действительны и четны, соотношения (2) можно представить в виде:
G
g
(f) =
2 ∫ B
с
(τ)cos (2πfτ)dτ
∞
0
,
В
с
(
τ) = 2 ∫ G
g
(f)cos (2πfτ)df
∞
0
.
Исходное сообщение перед его аналого-цифровым преобразованием
пропускается через идеальный ФНЧ (см. рис. 1). Фильтрация – это линейное
преобразование. Поэтому отклик х(t) ФНЧ на гауссовское воздействие будет
также гауссовским случайным процессом с нулевым математическим ожидани-
ем (x
ср
= М{х(t)} = 0) и мощностью, определяемой из соотношения:
P
x
= 2 ∫ G
g
(f) ∙ H
2
(f)df = 2 ∫ G
g
(f)df
f
ср
0
f
ср
0
,
где H(f) – амплитудно-частотная характеристика ФНЧ;
f
ср
–
частота среза фильтра.
Здесь учтено, что амплитудно-частотная характеристика идеального
ФНЧ равна единице в полосе частот [0, f
ср
] и нулю вне этой полосы. Кроме то-
го, его полоса пропускания принята равной ширине энергетического спектра
сообщения, поэтому частота среза ФНЧ равна f
ср
= f
g
. Это говорит о том, что
отклик ФНЧ представляет собой ограниченный по спектру сигнал сообщения.
В нем не содержится составляющих исходного сообщения с частотами f > f
g
.
Количественно потери при фильтрации сообщения характеризуются средне-
квадратичной ошибкой (СКО):
ξ
ф
2
= 2 ∫ G
g
(f)df = P
g
− P
x
∞
f
ср
,
где f
ср
= f
g
.
2.5.
Анализ характеристик и расчет параметров аналого-цифрового
преобразования сообщения
Аналого-цифровое преобразование исходного сообщения осуществляет-
ся в три этапа (см. рис. 1). Вначале первичный сигнал x(t) дискретизируется по
времени, далее отсчеты x(kΔt) квантуются по уровню, а затем квантованные
уровни v
k
j
кодируются, в результате чего формируется цифровой сигнал.
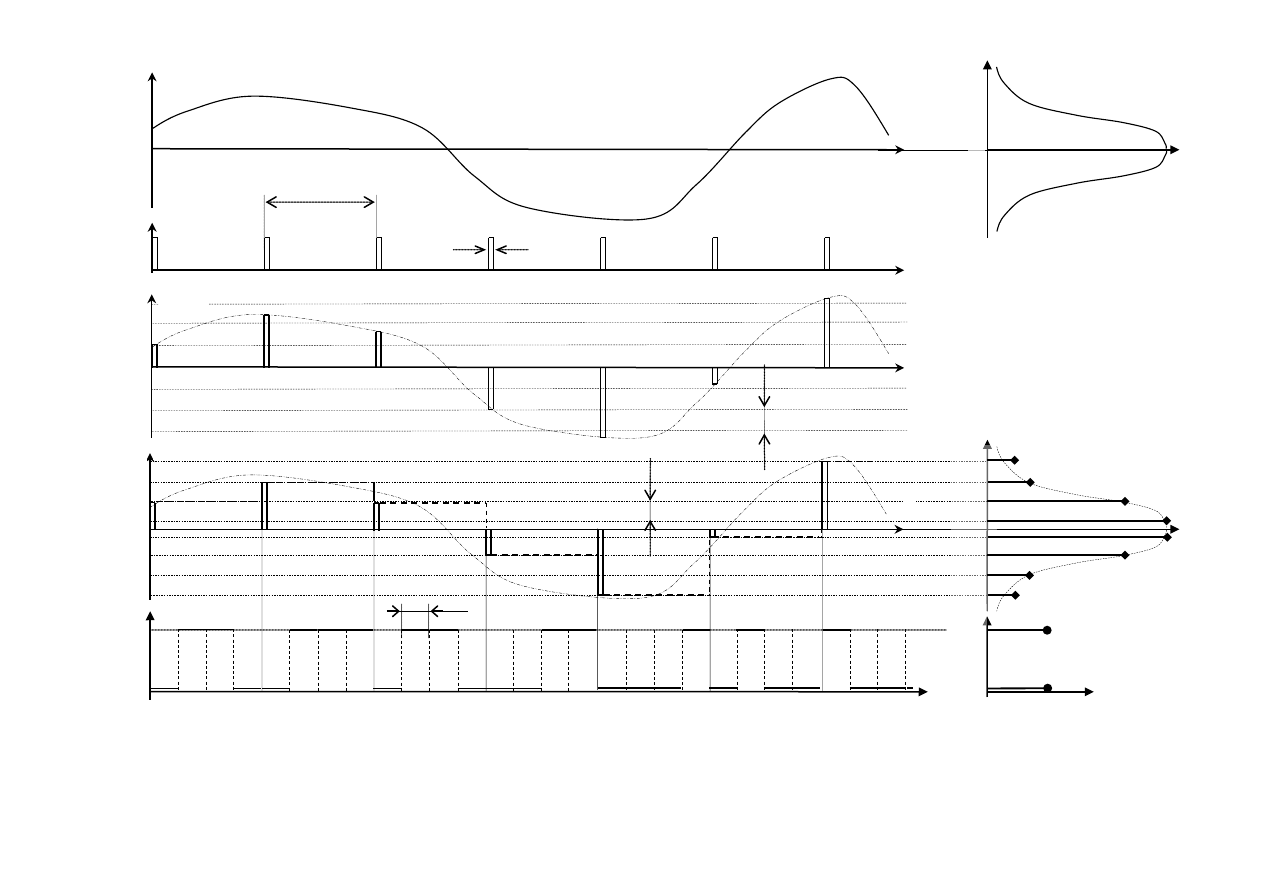
Все эти преобразования показаны на рис. 2, где показаны, также, функ-
ция распределения плотности вероятности первичного сигнала W
g
(x)
, распре-
деления вероятностей квантованного P(v
j
)
и кодированного P(b
m
)
сигналов.
В основе дискретизации лежит теорема В. А. Котельникова, которую
можно сформулировать в следующем виде [1, 4].
(2)

17
Любая непрерывная функция x(t), спектр которой не содержит состав-
ляющих с частотами выше f
В
, полностью определяется бесконечной последо-
вательностью своих отсчетов x(t
k
), взятых в моменты времени t
k
=
kΔt, крат-
ные интервалу дискретизации
Δt ≤
1
2????????
В
.
По исходным данным проекта сигнал х(t) на выходе идеального ФНЧ
соответствует требованиям данной теоремы. Поэтому его можно продискрети-
зировать, т.е. преобразовать из аналоговой формы х(t) в дискретно-аналоговую
x(
kΔt) с частотой дискретизации:
f
Д
=
1
Δ????????
= 2αf
В
= 2αf
g
,.
где α ≥ 1.
Дискретизатор может быть реализован в виде перемножителя двух
функций: непрерывного сообщения х(t) и периодической последовательности
дискретизирующих импульсов в виде δ-функций – δ
Т
(t) = ∑
δ(t − kΔt)
∞
k=−∞
(
см. рис 2,б).
Выходной сигнал дискретизатора х(kΔt) = х(t)· ∑
δ(t − kΔt)
∞
k=−∞
изоб-
ражен на рис. 2,в. Длительность реальных дискретизирующих импульсов τ
0
много меньше интервала (периода) дискретизации τ
0
<<
Δt и, поэтому, измене-
ниями амплитуды импульсов в интервале τ
0
часто пренебрегают.
В моменты t
k
=
kΔt импульсы на выходе дискретизатора могут принимать
любое значение из диапазона D
U
= U
max
– U
min
, называемого динамическим диапа-
зоном сообщения. В равномерном квантователе с шагом Δu этот диапазон разби-
вается на конечное число уровней квантования, состоящих из вектора уровней
сравнения U ∈ {u
i
,
i ∈ {1, L
�����}} и вектора уровней состояния V ∈ {v
j
,
j ∈ {1, L + 1
����������}}.
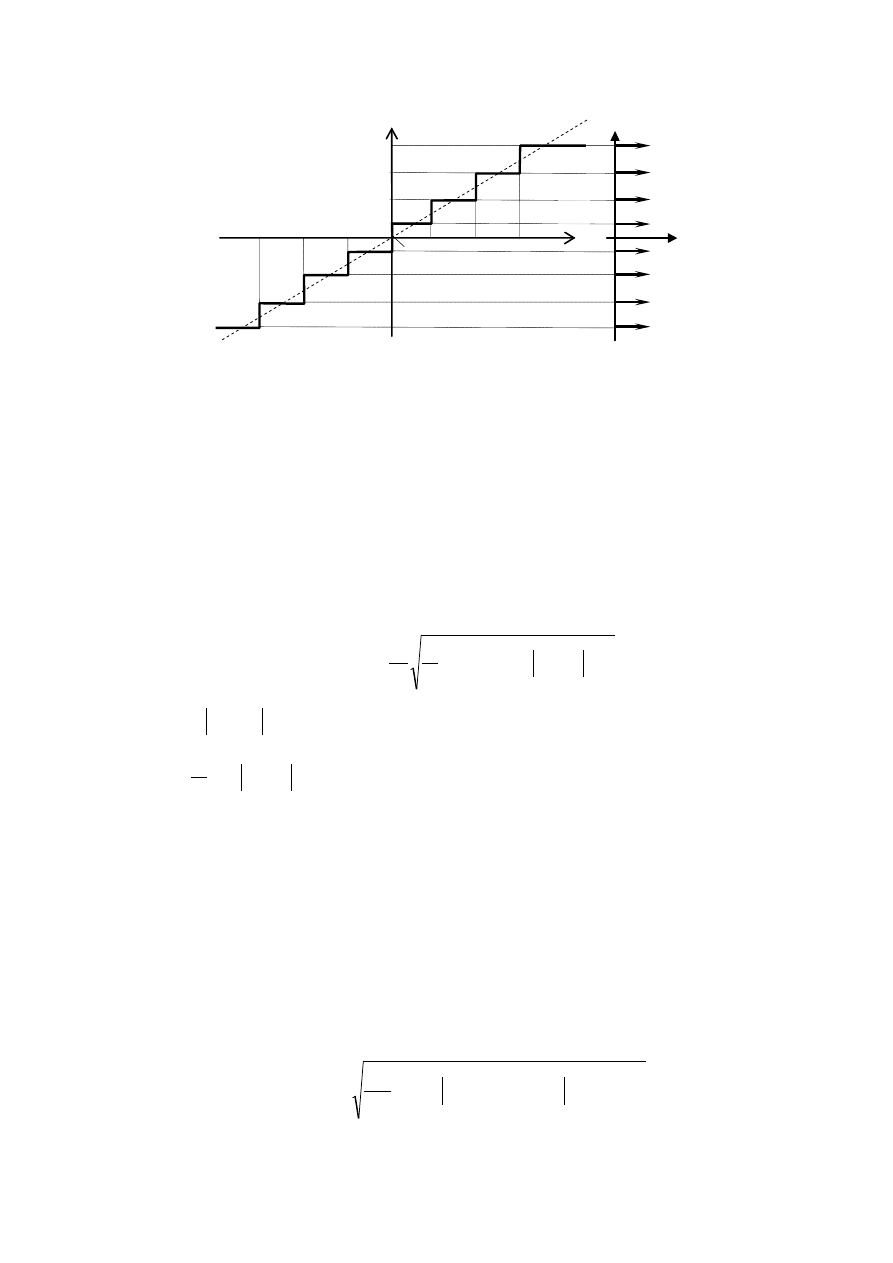
На рис. 2,в и 2,г показана процедура квантования в АЦП с μ = 3 (L = 7), а на рис. 3
–
вид амплитудной характеристики этого преобразователя.
Выбор параметров АЦП для случайных сигналов необходимо начинать с
определения шага (интервала) амплитудного квантования Δu, обеспечивающего
восстановление одномерной функции распределения плотности вероятности W
g
(x).
Функции распределения плотности вероятности W
g
(x
) квантуемого сиг-
нала соответствует характеристическая функция
( )
( )
∫
∞
∞
−
υ
=
υ
θ
dx
e
x
W
j
x
j
g
g
.
Если характеристическая функция (3) не содержит составляющих со
значениями переменной υ выше Λ
m
,
то она имеет вид:
( )
( )
Λ
>
Λ
≤
=
.
,
0
,
,
0
m
m
g
g
j
j
υ
υ
υ
θ
υ
θ
Для такого случайного сигнала может быть сформулирована теорема ампли-
тудного квантования для одномерной функции распределения плотности веро-
ятности [4] в следующем виде.
(3)
18
Рисунок 2 Аналого-цифровое преобразование сигнала
t
t
t
t
t /Δt
x(t)
δ
Т
(t)
v
k
j
x
W
g
(x)
P(v
j
)
v
j
u
L
u
L-1
…
u
2
u
1
v
L+1
v
L
…
v
2
v
1
v
L+1
v
L
…
v
2
v
1
0 t
1
t
2
t
3
… t
k
…
x(kΔt)
0 1 2 3 … k k+1
1
0
b
k
m
Δt
0 1 1 0 0 1 1 1 0 1 1 0 0 0 1 1 0 0 0 1 0 1 0 0 1 0 0 0
а)
б)
в)
г)
д)
Δ
U
Δ
U
τ
0
0
P(b
m
)
p(1)
p(0)
b
m
1
0
τ
сим
19
u
(L+1)/2
u
L-1
u
L
u
вых
y = q(x)
u
1
u
2
…
v
L+1
v
L
v
2
v
1
y
q
0
/
(x) =
dx/dy
u
вх
x
Рис. 3. Амплитудная характеристика аналого-цифрового преобразователя
Если характеристическая функция θ
g
(j
υ) случайного сигнала не имеет со-
ставляющих выше Λ
m
, то её функция распределения плотности вероятности
полностью определяется своими значениями W(ℓΔ
U
),
|
ℓ
|∈{0;
1;
2;
…}
, полученны-
ми с интервалом Δ
U1
≤ π/Λ
m
. Для восстановления исходного распределения необхо-
димо просуммировать квантованную случайную величину и независимую случай-
ную величину с равномерной характеристической функцией в полосе |υ| ≤ 2π/Δ
U1
.
Если квантуемый случайный процесс имеет неограниченную характери-
стическую функцию, то, в первом приближении, можно использовать её эффек-
тивную ширину.
Для характеристической функции θ
g
(j
υ) эффективная ширина определяется как
(
)
( )
∫
∞
∞
2
g
2
ср
2
1
ЭФФ
d
j
-
А
1
υ
υ
θ
υ
υ
=
θ
∆
π
,
где
( )
∫
∞
∞
2
g
d
j
A
ν
υ
θ
=
–
нормирующий множитель,
( )
∫
∞
∞
2
g
ср
d
j
А
1
υ
υ
θ
υ
=
υ
–
среднее значение характеристической частоты.
При выполнении условия:
Δ
U1
≤ π/Δθ
ЭФФ
,
где Δθ
ЭФФ
определяется соотношением (4), погрешность амплитудного кванто-
вания будет тем меньше, чем сильнее выполняется неравенство.
Для восстановления двумерной или условной функций распределения
плотности вероятности передаваемого первичного сигнала необходимо допол-
нительно выполнить условие [4]:
Δu
усл
≤ π/θ
m
усл
,
где θ
m
усл
определяется соотношением:
(
)
[
]
,
-
d
t
Δ
,
u
/
j
A
1
2
ср
у
∞
∞
2
1
усл
2
у
усл
m
∫
υ
υ
υ
θ
υ
=
θ
(4)

20
А
у
=
(
)
[
]
∫
∞
∞
2
1
усл
d
t
Δ
,
u
/
j
υ
υ
θ
–
нормирующий коэффициент;
(
)
[
]
∫
∞
∞
2
1
усл
c
р
y
d
t
Δ
,
u
/
j
υ
υ
θ
υ
=
υ
–
среднее значение условной характеристической функции.
При уменьшении интервала временной дискретизации Δt коррелирован-
ность отсчетов усиливается, дисперсия условной функции распределения
W
усл
(u
2
/u
1
,
∆t)
становится меньше, а условная характеристическая функция
θ
усл
[j(
ν
2
/u
1
,
∆t)] –
расширяется. Это определяет зависимость шага амплитудного
квантования от интервала временной дискретизации и с уменьшением Δt необ-
ходимый шаг квантования Δu
усл
уменьшается.
Выбор разрядности μ аналого-цифрового преобразователя (числа уров-
ней L) определяется наименьшим из значений ∆
U1
и Δu
усл
, а также допустимой
величиной погрешности усечения исходного распределения W(x) за счет огра-
ниченного динамического диапазона АЦП.
Выбором положения уровней характеристики АЦП при фиксированном
значении μ можно дополнительно минимизировать погрешность усечения, но
при этом усложняются АЦП и ЦАП (неравномерное квантование).
По заданию квантуется нормальный стационарный случайный процесс с
нулевым средним значением, дисперсией σ
2
и нормированной корреляционной
функцией r(kΔt), имеющий характеристическую функцию θ(υ) = exp(-0,5σ
2
υ
2
) и
условную характеристическую функцию
(
)
[
]
t
Δ
,
u
/
j
1
2
усл
υ
θ
=
( )
[
]
( )
{
}
2
1
2
2
2
2
t
r
u
j
t
r
-
1
5
,
0
-
exp
υ
∆
+
υ
σ
∆
.
Используя соответствующие соотношения, определим значения Δθ
эфф
и θ
m
усл
:
g
эфф
σ
2
2
π
θ =
∆
,
( )
(
)
1
-
2
g
уcл
m
Δ
-
1
σ
2
2
t
r
π
θ
=
.
Исходя из одномерного распределения, для обеспечения малого уровня
ошибок шаг квантования необходимо выбирать из условия
Δu
1
< π/Δθ
эфф
=
σ
g
/
2
.
У нормального случайного процесса эффективная ширина условной харак-
теристической функции θ
m
усл
не зависит от u
1
и интервал амплитудного квантова-
ния, для сохранения двумерного распределения, должен выбираться из условия
( )
.
2
-
1
Δ
2
усл
t
r
u
∆
<
σ
Шаг квантования Δu
усл
будет в η = Δ
U1
/Δu
усл
раз меньше шага, опреде-
ленного для одномерного распределения. В таблице 2 приведены выражения η
для нормального распределения и восьми видов корреляционных функций
(
восьми видов энергетических спектров) квантуемого процесса.
На рис. 4 приведены графики зависимостей значений η от интервала
временнόй дискретизации, из которых видно влияние формы энергетического
спектра на степень взаимосвязи интервалов Δu и Δt.