Добавлен: 15.11.2018
Просмотров: 2708
Скачиваний: 7

21
Таблица 2
Энергетический спектр
G(f)
Нормированная
корреляционная
функция
η
График
на ри-
сунке
G
0
�� β
2π�
2
+ f
2
�
2
�1 −
1
4????????� ???????????????????????? �−
1
4????????�
α = 1/2f
g
Δt ≥ 1
1
�1 − �1 − 0,25
???????? �
2
???????????????????????? �− 1
2????????�
�
1
>
,
f
f
0,
,
f
≤
f
,
f
f
-
1
G
g
g
g
0
(
)
(
)
2
/
/
sin
α
π
α
π
,
α = 1/2f
g
Δt ≥ 1
(
)
(
)
4
/
/
sin
-
1
1
α
π
α
π
2
G
0
� β
2π�
2
+ f
2
exp(-1/4
α)
α = 1/2f
g
Δt ≥ 1
1
�1 − ???????????????????????? �− 1
2????????�
�
3
> ,
f
f
0,
,
f
≤
f
,
G
g
g
0
(
)
(
)
α
π
α
π
/
/
sin
,
α = 1/2f
g
Δt ≥ 1
(
)
(
)
2
/
/
sin
-
1
1
α
π
α
π
4
G
0
sin �πf β
� �
f �1 − � fβ�
2
�
cos
2
(
π/3α)
α = 1/2f
g
Δt ≥ 1
1
�1 − ????????????????????????
4
� ????????
3????????�
�
5
G
0
4β
2
cos �πf 2β
� �
π
2
(β
2
− f
2
)
cos(
π/3α)
α = 1/2f
g
Δt ≥ 1
1
�1 − ????????????????????????
2
� ????????
3????????�
�
6
>
π
,
f
f
0,
,
f
≤
f
,
f
2
f
cos
G
g
g
g
0
(
)
(
)
2
/
2
-
1
/
cos
α
α
π
,
α = 1/2f
g
Δt ≥ 1
(
)
(
)
2
2
/
2
1
/
cos
-
1
1
α
α
π
7
G
0
exp �−
2π
2
f
2
β
2
�
exp �−
1
4α
2
�
α = 1/2f
g
Δt ≥ 1
1
�1 − exp �− 1
2α
2
�
�
8
Примечание. Значение G
0
определяется из условия:
P
g
=
2 ∫ G(f)
∞
0
df
Для определения шага квантования Δ
U
и уровней квантования u
i
, i
∈ 1, L
�����
учтем, что с вероятностью 0,997 гауссовский случайный процесс находится в
диапазоне D
g
= u
L
– u
1
= 6
σ
g
, где u
1
= – u
L
. (ввиду симметрии ФПВ). Если в этом
диапазоне разместить L–1 выходных уровня, а два уровня отвести на области
вне этого диапазона, т.е. v
1
< u
1
и v
L+1
> u
L
,
то разрядность АЦП можно рассчи-
тать следующим образом:
22
µ = �log
2
�
6σ
g
Δu
усл
+ 2��
,
где ]х[ означает ближайшее целое число, которое не меньше х.
Число входных уровней L можно определить из соотношения L = 2
μ
– 1,
а фактический шаг амплитудного квантования
Δ
U
=
6????????
????????
????????−1
.
Входные уровни квантования можно найти из выражения:
u
i
= −3σ
g
+ (i − 1)Δ
U
, i ∈ [1, L
�����].
Выходные уровни квантования определяются соотношениями:
v
j
= – 3
σ
g
+ (j – 1,5)
Δ
U
, j
∈[1, L + 1
����������].
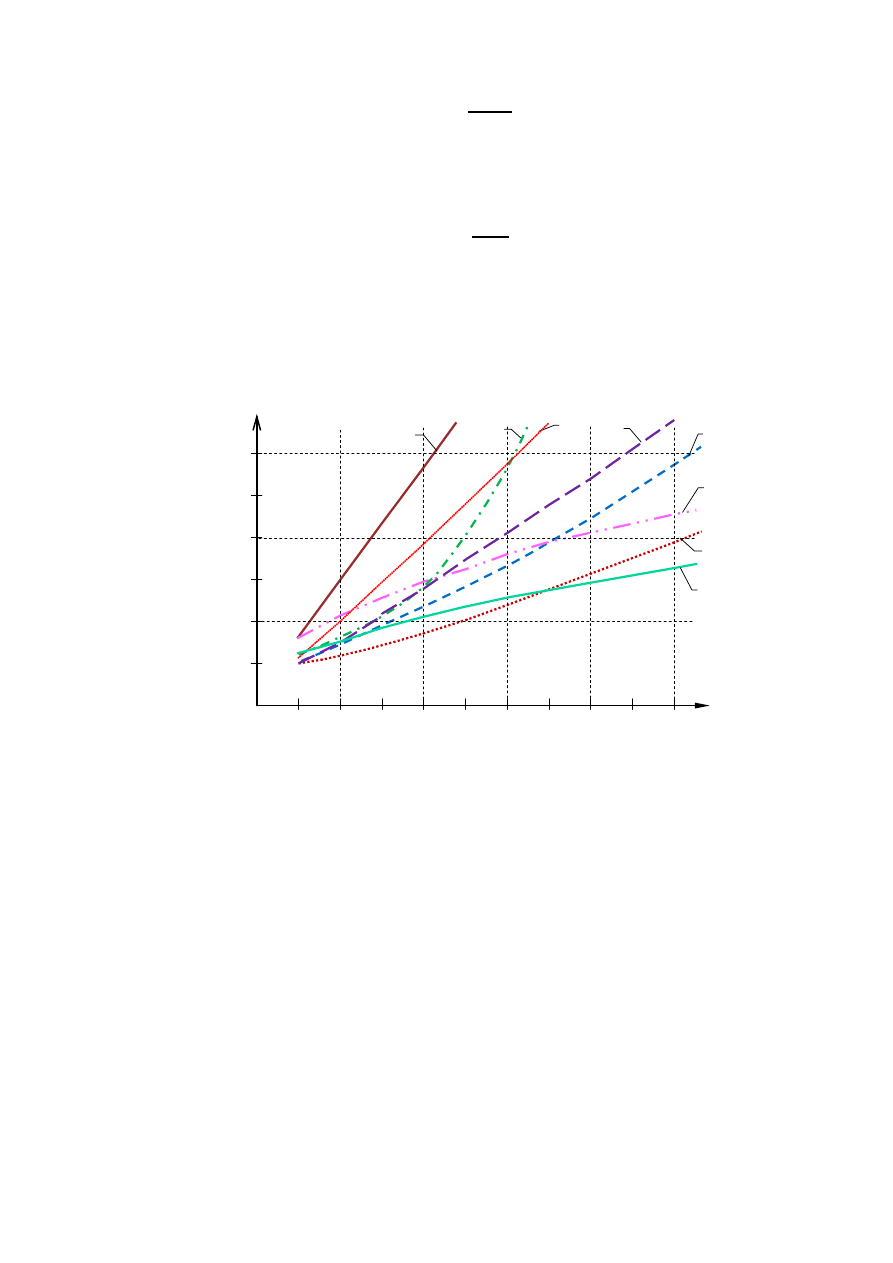
6
4
η
α
6
5
4
3
2
1
0
1 2 3 4 5 6 7 8 9 10
7
2
5
3
8
1
Рисунок 4. Зависимость шага амплитудного квантования от интервала времен-
нόй дискретизации
Таким образом, правило квантования отсчетов х(kΔt) состоит в следую-
щем. Если входной отсчет попадает в интервал u
i-1
<
х
k
< u
i
,
то на выходе кван-
тователя будет значение v
k
i
(см. рис 2,в и 2,г).
В процессе квантования возникает погрешность ξ
ki
= (v
k
i
– x
k
)
, называе-
мая шумом квантования. Вычислим среднеквадратическое значение шума
квантования (мощность шума квантования), осуществляя усреднение по мно-
жеству реализаций в моменты времени t
k
=
kΔt и полагая, что Δt >> τ
0
:
ξ̅
кв
2
= M�� (v
k
i
– x
k
)
2
�� = P
x
− 2B
xv
+ P
v
.
Здесь P
x
и Р
v
-
мощности переменной составляющей (дисперсии) входно-
го и выходного сигналов квантователя, соответственно; В
xv
–
коэффициент вза-
имной корреляции между этими сигналами. Усреднение M{۰} осуществляется
по ансамблю реализаций стационарного случайного процесса x(kΔt), поэтому ре-
зультат от номера отсчета k не зависит. Величину B
xv
для гауссовского процесса
находят из выражения:
(7)
(5)
(6)

23
B
xv
= &
σ
x
2
= &P
x
,
где постоянная & определяется следующим образом:
& = ∫ q
0
/
(x)W
g
(x)dx = Δu ∑ W
g
L
i=1
∞
−∞
(u
i
).
В этом соотношении q
0
/
(х) – производная от обратной характеристики
квантования x = q
0
(y
) (см. рис. 3) и W
g
(x) –
ФПВ гауссовской величины х, опре-
деляемая соотношением (1), в котором σ
g
2
=
Р
х
.
Подставляя (9) в (8), а результат
–
в (7), окончательно для СКО квантования получим:
ε�
кв
2
= P
x
(1 − 2&) + P
y
.
Мощность P
y
квантованного процесса y(kΔt) = v
ik
при нулевом среднем
значении процесса x(kΔt), равна:
P
y
= M(y
2
) = ∑ (v
i
)
2
p
i
L+1
i=1
= 2 ∑
(v
i
)
2
p
i
0,5(L+1)
i=1
= P
v
.
В данном соотношении распределение вероятностей p
i
,
i ∈{1, L + 1
����������},
случайной величины у
k
= v
ik
с учетом (5), рассчитывают по формуле:
p
i
= ∫
W
g
(z)dz = �Ф �
v
i+1
σ
g
� − Ф �
v
i
σ
g
��
v
i+1
v
i
,
где Ф(z) – табулированная функция Лапласа [5]:
Ф(z) =
1
√2π
∫ exp �−
t
2
2
�
z
−∞
dt.
Значения функции Ф(z) приведены в Приложении 4.
Интегральное распределение вероятности находят по выражению:
F
j
=
⎩
⎨
⎧
0, j < 1,
� p
i
j
i=1
,
1 ≤ j ≤ L + 1,
1, j > ???????? + 1.
Полагая, что отсчеты х(kΔt) на выходе дискретизатора некоррелированы
между собой, а для гауссовского процесса они независимы, определим инфор-
мационные характеристики выходного сигнала квантователя {y
k
}
, являющегося
входным сигналом L-ичного ДКС. Квантованная последовательность y
k
= v
k
j
,
???????? ∈ {1, ???????? + 1
����������}, с учетом независимости ее значений определяется одномерным
распределением вероятностей из выражения (10).
Энтропия H
y
количественно характеризует меру неопределенности о со-
общении {y
k
}
до его приема и определяется по формуле:
H
y
= − ∑
p
i
log
2
p
i
L+1
i=1
.
Значения – log
2
(p
i
)
и – р
i
log
2
(p
i
)
для некоторых значений p
i
приведены в Прило-
жении 5.
Производительность источника сообщений или скорость ввода инфор-
мации в ДКС определяется соотношением:
R
y
= H
y
/
Δt.
Избыточность выходных сообщений y
k
= v
k
j
,
???????? ∈ {1, ???????? + 1
����������}, равна:
ζ = (H
max
– H
y
)/H
max
,
где Н
max
-
максимальная энтропия. Для источника дискретных сообщений она равна
H
max
= log
2
(L+1).
В кодирующем устройстве (кодере) АЦП последовательность v
k
j
,
???????? ∈
{1, ???????? + 1
����������}, |k| = 0,1,2,... преобразуется в последовательность кодовых комбина-
(8)
(9)
(10)
(11)

24
ций b
k
µ
.
В системах цифровой связи широкое распространение получило дво-
ичное кодирование, когда кодовые символы принимают два значения b ∈ {0; 1}.
Собственно процедура двоичного безизбыточного блочного кодирова-
ния отсчетов {v
k
j
} состоит в следующем. Физические уровни {v
k
j
},
???????? ∈ {1, ???????? + 1
����������},
вначале нумеруются, т. е. заменяются десятичным числом от 1 до L + 1.
Например, для L = 7 номера уровней ???????? ∈ {1,8
����} принимают значения 1, 2, 3, 4, 5,
6, 7, 8
(см. рис. 2,в). Затем эти десятичные числа представляют в двоичной си-
стеме счисления с разрядностью µ. Это представление для значений μ = 3 и μ =
4
показано в таблице 3.
Таблица 3
v
i
v
1
v
2
v
3
v
4
v
5
v
6
v
7
v
8
Десятичное
число
1
2
3
4
5
6
7
8
b
i
3
001
010
011
100
101
110
111
000
b
i
4
0001
0010
0011
0100
0101
0110
0111
1000
Таким образом, в моменты времени t
k
=
kΔt уровни v
k
j
переводятся в ко-
довые комбинации b
k
µ
.
В результате формируется цифровой сигнал. Пример та-
кого преобразования приведен на рис. 2,г и рис.2,д для общего числа уровней
квантования L = 7.
Кодовым расстоянием d
lm
между двумя двоичными кодовыми комбина-
циями b
l
µ
и b
m
µ
называют результат поразрядного суммирования по модулю два
кодовых символов на j позициях (j∈ {1, ????????
�����}) сравниваемых кодовых комбинаций:
????????
????????????????
= ∑
????????
????????
????????
⊕
2
????????
????????
????????
????????
????????=1
,
????????, ???????? ∈ {1, ???????? + 1
����������}
Значения сумм по модулю два равны:
0
⊕
2
0 = 0; 0
⊕
2
1 = 1; 1
⊕
2
0 = 1; 1
⊕
2
1 = 0.
Таблица кодовых расстояний строится на основе (12), причем l – номер
строки, а m – номер столбца этой таблицы. Так как таблица симметрична отно-
сительно главной диагонали, на которой l = m, то в ней достаточно определить
только элементы выше главной диагонали.
Для вычисления вероятностей р(0) – появления нуля и р(1) –появления
единицы в сигнале ИКМ (см. рис. 2,д) обратимся к рис. 2,г. Справа показаны ве-
роятности р
i
,
???????? ∈ {1, ???????? + 1
����������} появления кодовых комбинаций, а на рис. 2,д сами ко-
довые комбинации b
k
µ
и справа – вероятности появления 0 и 1 [р(0) и р(1)]. Рас-
пределение вероятностей комбинации b
k
µ
относительно среднего уровня симмет-
рично. Среднее число единиц и нулей в кодовых комбинациях b
k
µ
,
соответствую-
щих этим уровням, также симметрично, т. е. n(0)
������ = n(1)
������, n(1)
������ = ∑ n
i
1
p
i
L+1
i=1
,
n(0)
������ = ∑ n
i
0
p
i
L+1
i=1
Так как среднее число нулей и среднее число единиц в цифровом сигнале
одинаково (это справедливо при гауссовской ФПВ сообщения и данного способа
кодирования), то и вероятности их появления одинаковы р(0) = р(1) = 0,5.
(12)
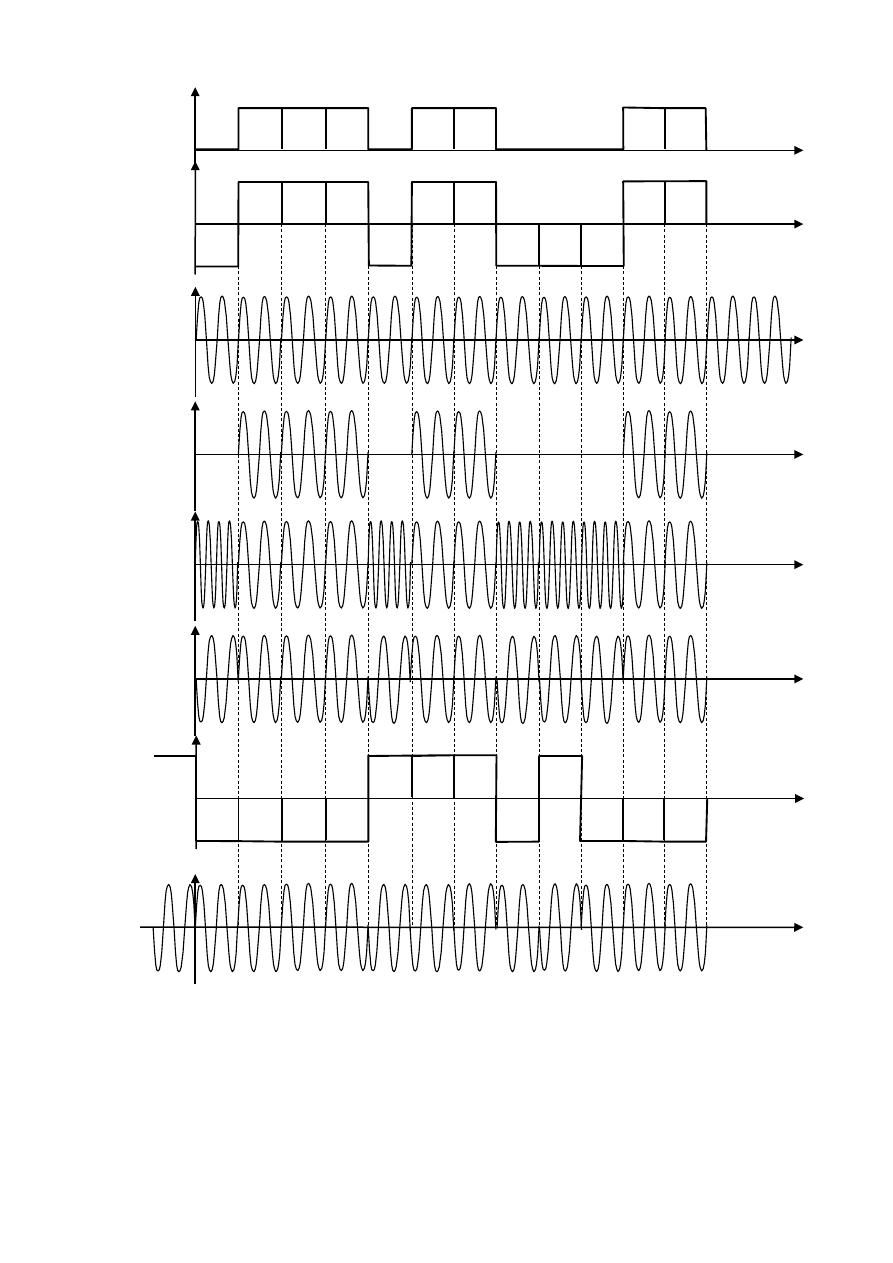
25
а)
+ + + + + + +
б)
– – – – –
в)
г)
д)
е)
+ + + +
ж)
– – – – – – – –
и)
Рис. 5. Сигналы при дискретной модуляции
Ширина спектра цифрового сигнала находится из следующих соображе-
ний. На интервале дискретизации Δt при блочном безизбыточном кодировании
должно разместиться µ элементарных кодовых символов. Следовательно, дли-
тельность одного кодового символа τ
сим
должна быть равна:
t
t
t
t
t
t
t
t
b
k
m
b
m
(t)
u
н
(t)
s
ДАМ
(t)
s
ДЧМ
(t)
s
ДФМ
(t)
b
от
m
(t)
s
ДОФМ
(t)