Добавлен: 08.11.2023
Просмотров: 341
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1.1 Матрица переноса 2 × 2 для слоисто-периодических структур
1.3 Сверхрешетки и одномерные фотонные кристаллы
2.Дефекты в слоисто-периодических структурах
2.1Классификация одиночных дефектов в одномерных фотонных кристаллах
2.2Влияние материала дефекта на вид спектра прохождения
МИНИСТЕРСТОВО ОБРАЗОВАНИЕ И НАУКИ РОССИСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ УЛЬЯНОВСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА
КУРСОВАЯ РАБОТА
на тему Метод передаточной матрицы 2х2
специальность:
Выполнил(а):
Студент(ка) группы____________________
_____________________/_______________
(Фамилия И.О. / подпись)
«_____» _________________20_____г.
Научный руководитель:
_____________________________________
(Степень, должность)
______________________/_______________
(Фамилия И.О. / подпись)
Оценка ______________________________
«_____» _________________20_____г.
Ульяновск, 2020 г
Оглавление
Аннотация 3
Введение 3
Передаточная матрица 5
1.1 Матрица переноса 2 × 2 для слоисто-периодических структур 5
1.2 Теорема Абелеса 10
1.3 Сверхрешетки и одномерные фотонные кристаллы 12
2.Дефекты в слоисто-периодических структурах 16
2.1Классификация одиночных дефектов в одномерных фотонных кристаллах 16
2.2Влияние материала дефекта на вид спектра прохождения 19
2.3 Одномерный фотонный кристалл с дефектом внедрения 21
Заключение 25
Список используемой литературы 26
Цель курсовой работы: Разобраться с методом матриц переноса применительно к описанию слоисто-периодических структур.
Задачи: 1. Понять, как связываются поля на границах раздела слоев. 2. Научиться применять граничные условия для получения дисперсионного соотношения. Выяснить в чем заключается смысл теоремы Флоке. 3. Получить матрицу переноса одного слоя, составить с помощью матриц – период структуры. Смоделировать – одномерный фотонный кристалл с двойным дефектом: инверсия + внедрение для исследования влияния материала дефекта на вид спектра прохождения.
Аннотация
В работе проведен обзор литературы и рассмотрен метод передаточной матрицы. Показано, как получить матрицу одного слоя и периода структуры, а также как с помощью метода матриц можно посчитать спектр коэффициента прохождения одномерного фотонного кристалла.
Введение
Физические свойства материалов, обладающих искусственно созданной дополнительной трансляционной симметрией, существенно отличаются от соответствующих параметров однородных тел. Замечательная особенность таких структур заключается в том, что имеется непосредственная аналогия между волновыми процессами в классических сверхрешетках и свойствами волновых функций электрона, движущегося в периодическом потенциале квантовой сверхрешетки.
В классических сверхрешетках в спектрах электромагнитных, звуковых, плазменных и т. п. волн образуются зоны пропускания и непропускания, в областях нарушения периодичности возникают специфические поверхностные волны, аналогичные поверхностным таммовским уровням или примесным уровням в полупроводниках. Наблюдение этих эффектов становится возможным, если длина волны меньше периода структуры.
Рассмотрим электродинамические свойства слоистых сред, состоящих из периодически повторяющихся слоев различных материалов, например, полупроводник-диэлектрик, ферромагнетик-полупроводник и т. д. Распространение волн в каждом слое полностью определяется материалом, из которого он состоит, а на границе между различными веществами поля связаны между собой определенным образом с помощью граничных условий. Поэтому весь слоисто-периодический образец участвует в формировании спектра колебаний. Можно сказать, что благодаря дополнительной трансляционной симметрии возникает новый материал, свойства которого зависят и определяются входящими в его состав средами. В наиболее простом случае, когда длины волн исследуемых колебаний существенно превышают толщины слоев, изучаемые материалы приобретают усредненные характеристики входящих в них веществ. Если же длина волны сравнима (или меньше) с толщиной слоя, то проявляются коллективные свойства их собственных колебаний. Они заключаются в том, что в спектрах электромагнитных волн возникают полосы прозрачности и полного внутреннего отражения в зависимости от частоты и угла распространения. Эти области аналогичны разрешенным и запрещенным энергетическим зонам для электронов в кристалле.
Слоистые периодические структуры, сверхрешетки и одномерные фотонные кристаллы нашли широкое применение в различных наукоемких областях. Структура может содержать до нескольких десятков и даже сотен слоев различных материалов. При большом количестве слоев в структуре для ее исследования широко используется матричные методы, позволяющие рассчитывать коэффициенты поглощения, отражения и пропускания при относительно небольших затратах машинного времени. Моделирование процесса взаимодействия слоистой структуры с излучением позволяет существенно сэкономить время и материалы на их изготовление, а также исследование свойств структуры. Исследования одномерных фотонно-кристаллических структур относятся к числу активно развивающихся направлений оптики. Они интересны для различных применений в оптической связи, лазерных технологиях как основа для создания новых устройств и приборов, благодаря наличию запрещенной зоны в заданной области частот и возможностью эффективного управления излучением.
Под одномерным (1D) фотонным кристаллом понимается периодическая плоскослоистая структура, в которой вдоль одного пространственного направления сформировано периодически неоднородное распределение диэлектрической проницаемости (ДП). Такая модуляция ДП приводит к возникновению зонной структуры энергетических уровней фотонов. Существует аналогия между фотонными и обычными кристаллами.
Идея управления излучением, находящимся в периодической структуре с модуляцией ДП, была сформулирована в 1987 году в работах Яблоновича Э. и Джона С., в которых и был предложен термин «фотонный кристалл». В отличие от обычного кристалла, где волна плотности вероятности электрона скалярна, поле электромагнитной волны носит векторый характер. Это потребовало разработки нового математического аппарата для расчета зонной структуры и привело к ряду отличительных свойств. Одним из таких важных свойств является пороговый характер возникновения запрещенной зоны - по глубине модуляции показателя преломления. В 1990 г. была впервые рассчитана зонная структура фотонного кристалла и было теоретически предсказано существование фотонной запрещенной зоны (ФЗЗ). Значительные технологические трудности в изготовлении решеток фотонных кристаллов для оптического диапазона длин волн привели к тому, что только в 2000 г. был впервые синтезирован фотонный кристалл, обладающий запрещенной зоной в ближней инфракрасной области спектра [1-5].
Передаточная матрица
1.1 Матрица переноса 2 × 2 для слоисто-периодических структур
Рассмотрим среды, представляющие собой двухслойную структуру, периодически повторяющуюся в пространстве. Смещение такой среды на целое число периодов не меняет вида структуры, поэтому отличие периодических материалов от однородных веществ состоит в дополнительной трансляционной симметрии.
Распространения волн в каждом из слоев можно описать с помощью волнового уравнения
| | (1.1) |
где
 — компонента поля волны,
— компонента поля волны,  - ее фазовая скорость в среде. Направим ось
- ее фазовая скорость в среде. Направим ось 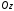
перпендикулярно границам раздела. Будем предполагать, что в плоскости слоев поля зависят только от одной координаты, и положим
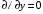 . Решение уравнения представим в виде
. Решение уравнения представим в виде 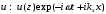 . Подставляя его в (1.1), получим
. Подставляя его в (1.1), получим| | (1.2) |
Так как фазовые скорости в слоях различны, то множитель
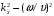 является периодической функцией координаты
является периодической функцией координаты  и принимает на периоде структуры два значения:
и принимает на периоде структуры два значения: 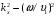 и
и 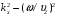 . Индексы 1 и 2 обозначают принадлежность к различным слоям. Таким образом, соотношение (1.2) является уравнением второго порядка с периодическим коэффициентом, это — уравнение Хилла. Для ступенчатой функции его решение может быть получено следующим образом. Представим поле на интервале
. Индексы 1 и 2 обозначают принадлежность к различным слоям. Таким образом, соотношение (1.2) является уравнением второго порядка с периодическим коэффициентом, это — уравнение Хилла. Для ступенчатой функции его решение может быть получено следующим образом. Представим поле на интервале 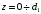 в виде
в виде 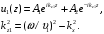 | (1.3) |
В области второго слоя
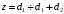
| | (1.4) |
На плоскости раздела должны выполняться граничные условия, состоящие в непрерывности как самого поля, так и его градиента. Так, например, на границе
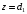 имеем
имеем 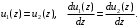 | (1.5) |
Кроме того, решение должно удовлетворять условию периодичности, т. е. поля на границах периода при
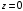 и
и 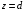 могут отличаться только на фазовый множитель
могут отличаться только на фазовый множитель| | (1.6) |
Соотношение (1.6) носит название
теоремы Флоке, сформулированной в 1883 году. В дальнейшем эта теорема была применена Блохом в 1928 году к решению уравнения в частных производных с периодическими коэффициентами. Решения, волны Блоха, легли в основу электронной теории твердого тела. Волновое число
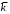 называется блоховским волновым числом. Физический смысл этой величины будет выяснен ниже.
называется блоховским волновым числом. Физический смысл этой величины будет выяснен ниже. Подставим выражения для полей (1.3) и (1.4) в соотношения (1.5) и (1.6):
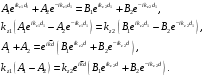 | (1.7) |
Эти формулы являются линейной однородной системой уравнений относительно неизвестных
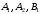 и
и 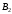 . Ее нетривиальное решение существует лишь в том случае, если детерминант системы равен нулю. Тогда
. Ее нетривиальное решение существует лишь в том случае, если детерминант системы равен нулю. Тогда 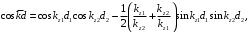 | (1.8) |
где
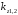 определяются формулами (1.3) и (1.4).
определяются формулами (1.3) и (1.4).Использованный выше метод можно значительно упростить, если ввести матрицы преобразования для каждого слоя. Обозначим
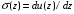 и из (1.3) получим
и из (1.3) получим 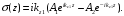 | (1.9) |
Выразим произвольные постоянные
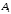 и
и 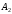 через значения полей при
через значения полей при  и подставим в соотношение (1.3) и (1.9). Результат запишем в матричном виде
и подставим в соотношение (1.3) и (1.9). Результат запишем в матричном виде 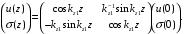 | |
Матрица, связывающая величины
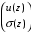 с
с 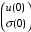 является унимодулярной, т. е. ее определитель равен единице. Представим поля в начале координат через их значения в произвольной точке
является унимодулярной, т. е. ее определитель равен единице. Представим поля в начале координат через их значения в произвольной точке