Файл: Метод передаточной матрицы 2х2.docx

слоя. Для этого необходимо найти обратную матрицу.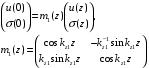

Матрица 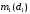связывает поля в начале слоя с полями в конце этого же слоя и называется матрицей преобразования. Для второго слоя аналогичным образом получим 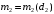. Так как поля при должны удовлетворять граничным условиям (1.5), то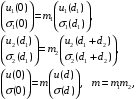

(1.10)

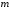- матрица преобразования одного периода структуры. Ее составляющие равны

(1.11)

Определитель этой матрицы также равен единице, так как 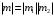. В этом легко убедиться непосредственным вычислением.

Понятие матрицы преобразования оказывается удобным для определения спектров собственных колебаний в безграничных, полуограниченных и ограниченных слоисто-периодических средах. Покажем, как с помощью матрицы преобразования 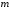может быть найдено дисперсионное соотношение для безграничной структуры. Для этого определим собственные векторы 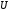и собственные числа матрицы :

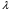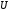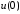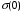Это уравнение совпадает с (1.10), если считать, что компонентами вектора являются и , а 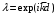. Уравнение для собственных чисел имеет вид:

---

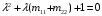и преобразуется в соотношение (1.8) заменой .

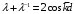Соотношение (1.8) позволяет выяснить смысл блоховского волнового вектора: видно, что в слоисто-периодической среде зависимость от поперечной координаты определяется не волновыми числами слоев 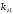и 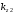, а величиной . Таким образом, блоховский вектор является усредненным по периоду структуры новым поперечным волновым числом. Его значение определяется из соотношения (2.8) с точностью до целого числа обратных волновых векторов 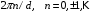. Поэтому полное решение волнового уравнения следует записать в виде суммы пространственных гармоник:

(1.12)

В заключение отметим, что матрица преобразования позволяет для нахождения характеристик структуры использовать систему уравнений второго порядка, а не четвертого, как в предыдущем случае (2.7). Еще больший выигрыш получается, если матрица имеет порядок выше второго.

1.2 Теорема Абелеса

Чтобы найти связь между полями в различных точках среды, отстоящих друг от друга на целое число периодов, необходимо найти произведение матрицей

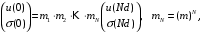где 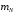- матрица преобразования ограниченной среды.

Формула, позволяющая возводить матрицу в целую степень, была получена Абелесом. Чтобы доказать ее, он использовал выражение для интерполяционного полинома (формула Сильвестра), которое позволяет записать полином 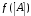от матрицы:

где 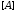- матрица с строками и

---

столбцами, 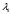- ее собственные значения, - единичная матрица. Для полинома 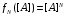получим

Эта формула выражает любую целую степень матрицы как функцию самой матрицы и ее собственных чисел. В частном случае, если 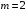, то

(1.13)

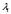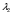где и - собственные значения матрицы , они определяются из уравнения

Предположим, что матрица - унимодулярная, тогда 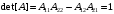, а корни этого уравнения — взаимно обратные величины. Обозначим 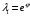, 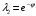. Тогда

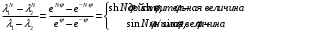(1.14)

выражение 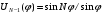называется полиномом Чебышева. Впервые на целесообразность применения функций Чебышева для анализа периодических четырехполюсников и ряда других задач указал, по-видимому, Пароди.

Окончательно формулу Абелеса получим, подставив соотношение (1.14) в (1.13):

(1.15)

где .

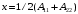Если исходная матрица 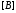- неунимодулярная, а ее определитель 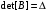, то формула Абелеса выглядит следующим образом:

(1.16)

---

где .

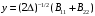1.3 Сверхрешетки и одномерные фотонные кристаллы

Сверхрешетки. Пристальный интерес исследователей, технологов и инженеров к периодическим структурам, состоящим из конечного числа слоев различных материалов например, полупроводниковых, магнитных, диэлектрических удерживается на протяжении многих десятилетий. Подобные мультислойные структуры получили название сверхрешеток. Характерные толщины слоев в сверхрешетках могут составлять от нескольких нанометров до нескольких микрон. Сверхрешеткой называется периодическая структура, состоящая из тонких чередующихся в одном направлении слоев, различающихся по своим физическим свойствам. Типичные широко используемые сверхрешетки изготавливают из полупроводниковых материалов. Такая структура, наряду с внутрикристаллическим потенциалом, обладает дополнительным потенциалом сверхрешетки, который обусловлен чередованием слоев различного полупроводника. Наличие потенциала сверхрешетки сущест-венно меняет зонную энергетическую структуру исходных полупроводников.

Поэтому сверхрешетку можно рассматривать как новый, синтезированный полупроводник, не существующий в природе и обладающий необычными свойствами. Подбором материала и состава чередующихся слоев можно в широких пределах варьировать зонную структуру сверхрешетки. Совокупность методов получения материалов с модифицированной зонной структурой лежит в основе так называемой "зонной инженерии".

К фотонным кристаллам принято относить структуры, у которых диэлектрическая проницаемость периодически меняется в пространстве с периодом, допускающим брэгговскую дифракцию света, что приводит к наличию в фотонных кристаллах «фотонной запрещённой зоны» (ФЗЗ).

Фотонные кристаллы, благодаря периодическому изменению коэффициента преломления, позволяют получить разрешённые и запрещённые зоны для энергий фотонов, аналогично полупроводниковым сверхрешеткам или кристаллам, в которых наблюдаются разрешённые и запрещённые зоны для энергий носителей заряда [1]. Практически это означает, что если на фотонный кристалл падает волна, длина волны которой соответствует запрещённой зоне данного фотонного кристалла, то она не может распространяться в фотонном кристалле и отражается обратно. Другими словами, фотонный кристалл выполняет функцию оптического фильтра.

---

Ниже приведены основные и часто используемые для описания свойств понятия, аналогичные для обычных и фотонных кристаллов:

кристалл - фотонный кристалл

электроны - фотоны

решетка атомов - решетка диэлектрика

периодический потенциал - периодически модулированная ДП

запрещенные зоны - фотонные запрещенные зоны

Фотонные кристаллы можно разделить на три основных класса в зависимости от характера изменения ДП или показателя преломления: одномерные (1D), двухмерные (2D) и трехмерные (3D).

В одномерных фотонных кристаллах ДП периодически изменяется в одном пространственном направлении. Такие фотонные кристаллы состоят из параллельных друг другу слоев различных материалов с разными показателями преломления. Возникновение фотонных запрещенных зон в структуре можно объяснить следующим образом. Периодическое распределение ДП приводит к тому, что электромагнитная волна, распространяющаяся в определенном направлении, испытывает отражение на структуре как на брэгговской решетке (или многослойном диэлектрическом зеркале). Такое «зеркало» отражает свет только в определенном диапазоне длин волн, положение которого зависит от периода решетки. Свет с длиной волны, лежащей в этом диапазоне не может распространяться в соответствующем направлении.

Указанное свойство в оптическом диапазоне широко используется для создания многослойных экранов (брэгговских зеркал) и фильтров из прозрачных слоёв, отличающихся показателем преломления. Такие плоскослоистые структуры могут служить как зеркала или как многополосные фильтры с окнами прозрачности и непропускания [2,5]. Для проявления селективных свойств толщины слоёв должны быть порядка четверти длины волны, что для оптического диапазона соответствует сотням нанометров. Получение сильно селективных свойств на небольшом числе слоёв требует большого различия их ДП. Однако у оптически прозрачных материалов такое различие невелико. Поэтому возникает технологическая задача синтеза слоёв с заданными свойствами, т.е. значениями ДП.

Брэгговские зеркала. Тонкие брэгговские зеркала представляют собой структуру, состоящую из чередующейся последовательности слоев из оптических (прозрачных) материалов с разным показателем преломления. Толщина каждого оптического слоя соответствует четверти центральной длины волны брэгговского зеркала. На границе между слоями с разными показателями преломления падающий пучок отражается (рис. 1).

---