Добавлен: 08.11.2023
Просмотров: 344
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1.1 Матрица переноса 2 × 2 для слоисто-периодических структур
1.3 Сверхрешетки и одномерные фотонные кристаллы
2.Дефекты в слоисто-периодических структурах
2.1Классификация одиночных дефектов в одномерных фотонных кристаллах
2.2Влияние материала дефекта на вид спектра прохождения
| | |
В общем случае компоненты и представляют собой интегральные операторы
| | |
Для плоских волн они сводятся к функциям, зависящим от частоты и волнового вектора ,
| | (2.3) |
Тензоры и описывают временную и пространственную дисперсии, которыми характеризуется исследуемая среда. Эти функции определяются из материальных уравнений. Ряд свойств тензоров и может быть установлен в общем виде, однако это не входит в нашу задачу. Отметим также, что в дальнейшем исследуются немагнитные полупроводники, поэтому
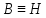 и
и 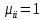 .
.Изучение свойств классических сверхрешеток начнем с уравнений (2.1)- (2.3), не конкретизируя вида функций . Матричный метод описания слоистых сред, позволяет получить дисперсионное уравнение, описывающее свойства периодических систем, образованных различными веществами: диэлектриками, полупроводниками и т. п., для которых предполагается, что их тензор диэлектрической проницаемости не имеет пространственной дисперсии.
Рассмотрим плоскослоистую периодическую структуру, период которой составлен из двух материалов, различающихся толщинами слоев и диэлектрическими проницаемостями и . Вдоль оси слои предполагаются однородными, и поэтому зависимость от координаты можно исключить из уравнений, положив . Если тензор имеет вид
| | |
То уравнения Максвелла могут быть представлены следующим образом (зависимость от времени выбрана в виде ):
ТЕ-волны:
| | (2.4) |
ТМ-волны:
| | (2.4a) |
Отметим, что ТЕ-волна связана только с одной компонентой тензора , а ТМ-волна — с четырьмя. В однородной среде в одноосной оптической среде и в гиротропной . Изучим свойства решеток, составленных из однородных слоев, диэлектрическая проницаемость которых является константой.
Для получения передаточной матрицы необходимо сформулировать граничные условия для полей на плоскостях раздела слоев. Из уравнений Максвелла для тангенциальных составляющих электрического поля имеем условия непрерывности:
ТЕ-волны:
| | (2.5) |
ТМ-волны:
| | |
Далее получим условия непрерывности для компонент магнитного поля:
ТЕ-волны:
| | (2.6) |
ТМ-волны:
| | |
Заметим, что в проводящих средах эти условия могут нарушаться из-за возникновения поверхностных токов или зарядов.
Представим поля в виде блоховских функций, получим матрицы преобразования
| | (2.7) |
где
| | |
| | (2.8) |
где
| | |
- поперечные волновые числа первого и второго слоев. Теперь дисперсионные уравнения имеют вид:
для ТЕ-колебаний:
| | (2.9) |
Для ТМ-колебаний:
| | (2.10) |
Предельные переходы к однородной среде получаются, если толщину одного из слоев устремить к нулю, или когда диэлектрические проницаемости обоих слоев одинаковы . При этом , т. е. блоховское волновое число переходит в поперечное волновое число однородной среды. Это означает, что в сверхрешетке выполняет роль компоненты усредненного волнового вектора вместо и .
Заключение
В работе проведен литературный обзор источников по теме исследования. Показано, что матричные методы позволяют моделировать одномерные фотонные кристаллы с любыми дефектами и определять спектры коэффициентов отражения и прохождения. В работе представлена классификация одиночных дефектов в одномерных фотонных структурах. Продемонстрировано получение матрицы одного слоя и периода структуры.
Список используемой литературы
[1] Басс Ф.Г., Булгаков А.А., Тетервов А.П. Высокочастотные свойства полупроводников со сверхрешетками.– М.: Наука Гл.ред. физ-мат. лит., (Физика полупроводников и полупроводниковых приборов), 1989.– 288 с.
[2] Бреховских Л.М. Волны в слоистых средах. – М.: Наука. 1973. – 343 с.
[3] Бриллюэн Л., Пароди М. Распространение волн в периодических структурах. – М.: И.Л. 1959. – 457 с.
[4] Борн М., Вольф Э. Основы оптики. – М.: Наука. 1973.– 720 с.
[5] Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. — М.: Наука 1979. — 383 с.