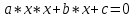Файл: Методические указания по организации практических занятий и самостоятельной работы по мдк. 02. 01 Технология разработки программного обеспечения.docx

Соответствующие диаграммы состояний имеют вид

Для создания диаграмм состояний, которые входят в состав составного состояния, нужно:

1. 
   Щелкнуть правой кнопкой мыши по Составному состоянию и выбрать пункт Схема.
   
2. 
   Либо, в Проводнике по моделям выделить название составного состояния и создать новую страницу с помощью кнопки .
   

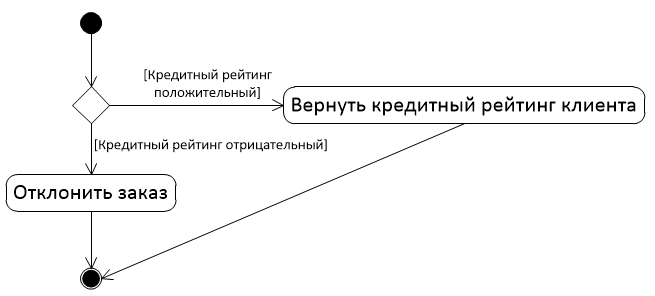
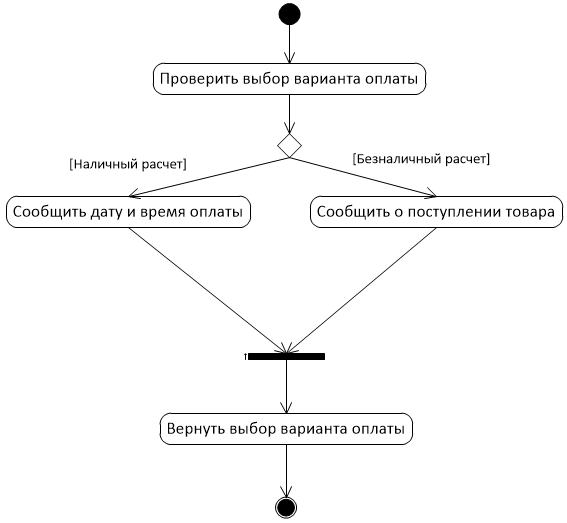
Задание практической работы

По образцу построить диаграмму состояний.
Задание самостоятельной работы

В соответствии с индивидуальным вариантом, построить диаграмму состояний.

Перечень индивидуальных вариантов приведен в приложении А.

Отчет по практическому занятию выполняется в формате MS Word, который содержит экранные формы моделей согласно заданию.
Контрольные вопросы

1. 
   Каково назначение диаграммы состояний?
   
2. 
   Назовите основные элементы диаграммы состояний.
   
3. 
   Как создать диаграмму состояний в VISIO?
   
4. 
   В чем отличие диаграммы классов и состояний?
   

---

Практическая работа №6

Построение диаграммы Деятельности и диаграммы Последовательности
Цель: изучение основ создания диаграмм деятельности на языке UML, получение навыков построения диаграмм деятельности, применение приобретенных навыков для построения объектно-ориентированных моделей определенной предметной области. Изучение основ создания диаграмм последовательностей на языке UML, получение навыков построения диаграмм последовательностей, применение приобретенных навыков для построения объектно-ориентированных моделей определенной предметной области.
Форма отчета:

Диаграмма Деятельности и диаграмма Последовательности с описанием процесса построения диаграмм.
Краткие теоретические сведения

Построение диаграммы Деятельности

При моделировании поведения проектируемой или анализируемой системы возникает необходимость не только представить процесс изменения ее состояний, но и детализировать особенности алгоритмической и логической реализации выполняемых системой операций. Традиционно для этой цели использовались блок-схемы или структурные схемы алгоритмов. Каждая такая схема акцентирует внимание на последовательности выполнения определенных действий или элементарных операций, которые в совокупности приводят к получению желаемого результата.

Алгоритмические и логические операции, требующие выполнения в определенной последовательности, окружают нас постоянно. Например, чтобы позвонить по телефону, нам предварительно нужно снять трубку или включить его. Для приготовления кофе или заваривания чая необходимо вначале вскипятить воду. Чтобы выполнить ремонт двигателя автомобиля, требуется осуществить целый ряд нетривиальных операций, таких как разборка силового агрегата, снятие генератора и некоторых других.

C увеличением сложности системы строгое соблюдение последовательности выполняемых операций приобретает все более важное значение. Если попытаться заварить кофе холодной водой, то мы можем только испортить одну порцию напитка. Нарушение последовательности операций при ремонте двигателя может привести к его поломке или выходу из строя. Еще более катастрофические последствия могут произойти в случае отклонения от установленной последовательности действий при взлете или посадке авиалайнера, запуске ракеты, регламентных работах на АЭС.

---

Для моделирования процесса выполнения операций в языке UML используются так называемые диаграммы деятельности. Применяемая в них графическая нотация во многом похожа на нотацию диаграммы состояний, поскольку на диаграммах деятельности также присутствуют обозначения состояний и переходов. Отличие заключается в семантике состояний, которые используются для представления не деятельностей, а действий, и в отсутствии на переходах сигнатуры событий. Каждое состояние на диаграмме деятельности соответствует выполнению некоторой элементарной операции, а переход в следующее состояние срабатывает только при завершении этой операции в предыдущем состоянии. Графически диаграмма деятельности представляется в форме графа деятельности, вершинами которого являются состояния действия, а дугами – переходы от одного состояния действия к другому.

Таким образом, диаграммы деятельности можно считать частным случаем диаграмм состояний. Основным направлением использования диаграмм деятельности является визуализация особенностей реализации операций классов, когда необходимо представить алгоритмы их выполнения. При этом каждое состояние может являться выполнением операции некоторого класса либо ее части, позволяя использовать диаграммы деятельности для описания реакций на внутренние события системы.

В контексте языка UML деятельность (activity) представляет собой некоторую совокупность отдельных вычислений, выполняемых автоматом. При этом отдельные элементарные вычисления могут приводить к некоторому результату или действию (action). На диаграмме деятельности отображается логика или последовательность перехода от одной деятельности к другой, при этом внимание фиксируется на результате деятельности. Сам же результат может привести к изменению состояния системы или возвращению некоторого значения.
Состояние действия и деятельности

Состояние деятельности (activity state) – состояние в графе деятельности, которое служит для представления процедурной последовательности действий, требующих определенного времени. Переход из состояния деятельности происходит после выполнения специфицированной в нем ду-деятельности, при этом ключевое слово do в имени деятельности не указывается. Состояние деятельности не может иметь внутренних переходов, поскольку оно является элементарным.

---

Состояния деятельности могут быть подвергнуты дальнейшей декомпозиции, вследствие чего выполняемую деятельность можно представить с помощью других диаграмм деятельности. Состояния деятельности не являются атомарными, то есть могут быть прерваны. Предполагается, что для их завершения требуется заметное время.

Состояние деятельности можно представлять себе, как составное состояние, поток управления которого включает только другие состояния деятельности и действий.

Состояние действия (action state) является специальным случаем состояния с некоторым входным действием и, по крайней мере, одним выходящим из состояния переходом. Этот переход неявно предполагает, что входное действие уже завершилось. Состояние действия не может иметь внутренних переходов, поскольку оно является элементарным. Обычное использование состояния действия заключается в моделировании одного шага выполнения алгоритма (процедуры) или потока управления.

Графически состояние действия изображается фигурой, напоминающей прямоугольник, боковые стороны которого заменены выпуклыми дугами. Внутри этой фигуры записывается выражение действия (action-expression), которое должно быть уникальным в пределах одной диаграммы деятельности.



Действие может быть записано на естественном языке, некотором псевдокоде или языке программирования. Никаких дополнительных или неявных ограничений при записи действий не накладывается. Рекомендуется в качестве имени простого действия использовать глагол с пояснительными словами. Если же действие может быть представлено в некотором формальном виде, то целесообразно записать его на том языке программирования, на котором предполагается реализовывать конкретный проект.

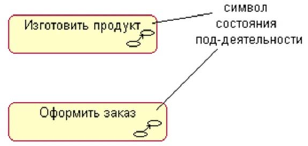
Иногда возникает необходимость представить на диаграмме деятельности некоторое сложное действие, которое, в свою очередь, состоит из нескольких более простых действий. В этом случае можно использовать специальное обозначение так называемого состояния поддеятельности (subactivity state). Такое состояние является графом деятельности и обозначается специальной пиктограммой в правом нижнем углу символа состояния действия (рис. 2). Эта конструкция может применяться к любому элементу языка UML, который поддерживает «вложенность» своей структуры. При этом пиктограмма может быть дополнительно помечена типом вложенной структуры.

---

Каждая диаграмма деятельности должна иметь единственное начальное и единственное конечное состояния. Они имеют такие же обозначения, как и на диаграмме состояний. При этом каждая деятельность начинается в начальном состоянии и заканчивается в конечном состоянии. Саму диаграмму деятельности принято располагать таким образом, чтобы действия следовали сверху вниз. В этом случае начальное состояние будет изображаться в верхней части диаграммы, а конечное – в ее нижней части.

Переходы

При построении диаграммы деятельности используются только такие переходы, которые срабатывают сразу после завершения деятельности или выполнения соответствующего действия. Этот переход переводит деятельность в последующее состояние сразу, как только закончится действие в предыдущем состоянии. На диаграмме такой переход изображается сплошной линией со стрелкой.

Если из состояния действия выходит единственный переход, то он может быть никак не помечен. Если же таких переходов несколько, то сработать может только один из них. Именно в этом случае для каждого из таких переходов должно быть явно записано сторожевое условие в прямых скобках. При этом для всех выходящих из некоторого состояния переходов должно выполняться требование истинности только одного из них. Подобный случай встречается тогда, когда последовательно выполняемая деятельность должна разделиться на альтернативные ветви в зависимости от значения некоторого промежуточного результата. Такая ситуация получила название ветвления, а для ее обозначения применяется специальный символ.

Графически ветвление на диаграмме деятельности обозначается небольшим ромбом, внутри которого нет никакого текста. В этот ромб может входить только одна стрелка от того состояния действия, после выполнения которого поток управления должен быть продолжен по одной из взаимно исключающих ветвей. Принято входящую стрелку присоединять к верхней или левой вершине символа ветвления. Выходящих стрелок может быть две или более, но для каждой из них явно указывается соответствующее сторожевое условие в форме булевского выражения.

В качестве примера рассмотрим фрагмент известного алгоритма нахождения корней квадратного уравнения. В общем случае после приведения уравнения второй степени к каноническому виду:

---