ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.03.2024
Просмотров: 1495
Скачиваний: 0
СОДЕРЖАНИЕ
Тема 6. Смертность, средняя ожидаемая продолжительность жизни, самосохранительное поведение
Тема 7. Естественный рост и воспроизводство населения
Тема 8. Демографическое прогнозирование
Тема 1 Предмет, задачи и методы демографии
1.1. Краткая история становления демографии
1.4. Методы исследования в демографии
1.5. Специализация внутри демографии
Тема 2 Источники информации о населении и демографических процессах
2.1.1. Определение переписи населения
2.1.2. Основные принципы современной переписи населения
2.1.3. Краткая история переписей населения в мире
2.1.4. Переписи населения в России, ссср и снова в России
Учеты населения (ревизии) в России в XVIII
2.1.5. Программа переписи населения
2.1.6. Программа Всероссийской переписи населения 1999 года
Вопрос 6: гражданство. Вопрос представляется мне простым и не требующим пояснений.
2.1.7. Правовая основа переписи населения
2.1.8. Критический момент переписи населения (или момент счета населения)
2.1.9. Категории населения, учитываемые при переписях населения
2.1.10. Программа разработки материалов
2.1.11. Массово-разъяснительная работа среди населения
2.2. Текущий статистический учет событий естественного движения населения
2.3. Текущие регистры (списки, картотеки) населения
2.4. Выборочные и специальные обследования
Тема з Численность и структура населения
3.2. Структура населения по полу
Половая структура населения России3
3.3. Возрастная структура населения
3.3.1. Половозрастные пирамиды
3.3.2. Связь возрастной структуры с режимом воспроизводства населения
Режиму воспроизводства населения
3.3.3. Демографическое старение населения
Индекс демографической старости населения России (в процентах)
3.4. Брачная структура населения
3.4.1. Методы реального и условного поколения
Число лет, прожитых в определенном брачном состоянии
3.5 Семейная структура населения
Распределение семей в России по размерам (по итогам
Тема 4 Общие коэффициенты естественного движения населения
Тема 5 Рождаемость и репродуктивное поведение
Формула расчета специального коэффициента рождаемости выглядит так:
5.2. Возрастные коэффициенты рождаемости
5.3. Рождаемость и плодовитость
5.4. Графическое изображение возрастных коэффициентов рождаемости
Возрастные коэффициенты рождаемости (ссср (1926—1927, 1958—1959 гг.), России (1995 г.)
5.5. Брачная и внебрачная рождаемость
5.6. Суммарный коэффициент рождаемости
Возрастные и суммарный коэффициенты рождаемости в России в 1995 г.
5.8. Демографическая типология семей по числу рожденных детей
5.9. Учет уровня смертности при оценке величины суммарного коэффициента рождаемости
5.10. Динамика уровня рождаемости в мире
Общий и суммарный коэффициенты рождаемости в мире и отдельных странах, 1960—1964 и 1998 гг.
5.11. Динамика уровня рождаемости в России, ссср и снова в России
Компоненты изменений общего коэффициента рождаемости в
Россия, все население, 1995 г.
5.13. Индекс гипотетического минимума естественной рождаемости (гмер)
Минимальные коэффициенты брачной естественной рождаемости, принятые в модели гмер за стандарт
Факторная структура изменений общего коэффициента
5.14. Краткая история исследований факторов рождаемости
Специальные коэффициенты брачной рождаемости в ряде европейских столиц в конце XIX в. (в расчете на
1000 Замужних женщин в возрасте 15—49 лет)2
5.15. Изучение репродуктивного поведения
5.16. Показатели репродуктивного поведения в переписях населения
Желаемое и ожидаемое число детей у женщин России
5.17. Теория демографического перехода и интерпретация дифференциальной рождаемости
5.18. Исторические причины развития массовой малодетности семей
5.20. Социальная и демографическая политики: взаимосвязь и различия целей
Тема 6 Смертность, средняя ожидаемая продолжительность жизни, самосохранительное поведение
6.1. Возрастные коэффициенты смертности
6.2. Коэффициент младенческой смертности
Структура уровня младенческой смертности в России по основным классам причин смерти
6.3. Применение индексного метода в анализе динамики общего коэффициента смертности
6.4. Методы стандартизации коэффициентов
Расчет факторов изменения уровня смертности в России в 1990—1995 гг.
6.4.1. Прямой метод стандартизации
6.4.2. Косвенный метод стандартизации
6.5. Вероятностные таблицы смертности (чаще
6.6. Расчет кратких таблиц смертности
Расчет таблиц смертности мужского населения России в 1995 году
6.7. Уровень средней ожидаемой продолжительности
6.8. Средняя интервальная продолжительность предстоящей жизни
Для достигших начала каждого возрастного интервала
6.9. Показатели смертности по причинам смерти
6.10. Социальный прогресс и изменение структуры уровня смертности по причинам смерти
6.11. Факторы уровня смертности и средней продолжительности жизни
6.12. Самосохранительное поведение
Тема 7 Естественный рост и воспроизводство населения
7.1. Общий коэффициент естественного прироста
7.2. Показатели воспроизводства населения
7.3. Соотношение уровней рождаемости и смертности в динамике воспроизводства населения
Тема 8 Демографическое прогнозирование
8.1. Прогнозирование общей численности населения
8.2. Прогнозирование половозрастной структуры населения
Иллюстративный прогноз численности и половозрастной структуры населения России до
2027 Года методом возрастной передвижки
Иллюстративный прогноз числа рождений в России в 1998—2026 гг.
8.3. Разработка гипотез о вероятных изменениях демографических тенденций в прогнозном периоде
Приложение Программа курса «Демография» Тема 1. Предмет, задачи и методы демографии
Тема 2. Источники информации о населении и демографических процессах
Тема 3. Численность и структура населения
Тема 4. Показатели естественного движения населения
Тема 5. Рождаемость и репродуктивное поведение
Тема 6. Смертность, средняя ожидаемая продолжительность жизни, самосохранительное поведение
Тема 7. Естественный рост и воспроизводство населения
Тема 8. Демографическое прогнозирование
Распределение учебных часов по курсу «Демография»
Тема 6. Смертность, средняя ожидаемая продолжительность жизни, самосохранительное поведение
6.4.2. Косвенный метод стандартизации
Если в распоряжении исследователя имеются данные о возрастной структуре сравниваемых совокупностей населения, но неизвестны возрастные коэффициенты смертности и нет исходных данных для их расчета, то можно произвести стандартизацию коэффициентов косвенным методом. В этом случае за стандарт принимаются возрастные коэффициенты какого-либо населения, которые можно найти в статистических справочниках.
При этом методе стандартизация производится косвенно, т.е. мы задаемся вопросом, каким было бы общее число умерших, если бы возрастные коэффициенты смертности во всех сравниваемых группах были бы одинаковыми и именно такими как в стандарт-населении (т.е. в населении, принятом за стандарт). Это рассуждение можно выразить в виде формулы: M = Мх = Px mx, или, если эту формулу пересказать словами, она означает, что общее число умерших M равно сумме умерших во всех возрастных группах Мx, которая, в свою очередь, может быть представлена в виде суммы произведений численности населения каждой возрастной группы на соответствующий ей возрастной коэффициент смертности. По условию нам известны возрастные структуры сравниваемых групп населения, но неизвестны их возрастные коэффициенты смертности. Поэтому заменяем неизвестные возрастные фактические коэффициенты смертности произвольно подобранными (из справочника, относящимися к любому населению, о котором мы все же априори знаем, что его повозрастная смертность не слишком отличается от смертности в сравниваемых населениях). Используя возрастные коэффициенты смертности населения, принятого за стандарт, получаем так называемые условные числа умерших, т. е. числа умерших, какими они были бы при условии, что повозрастная смертность во всех сравниваемых группах населения одинакова и такая, как в населении, принятом за стандарт. В виде формулы это можно изобразить таким образом: М0 = Px х тх0, где M0 условное число умерших, Рх — фактические возрастные структуры сравниваемых населений, и тх0 возрастные коэффициенты смертности населения, принятые за стандарт. Сравнивая затем фактическое число умерших в каждом населении с соответствующим этому населению условным числом умерших, получаем индекс, показывающий, насколько фактическая повозрастная смертность в сравниваемом населении (или группе населения) отличается от смертности стандарт-населения. Умножая этот индекс на общий коэффициент смертности стандарт-населения (т0), получаем в итоге стандартизованный коэффициент смертности для каждого сравниваемого населения. Окончательно наши рассуждения удобно выразить следующей формулой:
![]() (6.8)
(6.8)
где тCТ — стандартизованный общий коэффициент смертности; Рх — возрастные группы сравниваемого населения; М — общее число умерших в сравниваемом населении; тх0 — возрастные коэффициенты смертности населения, принятого за стандарт, и т0 — общий коэффициент смертности населения, принятого за стандарт.
Но расчет самих стандартизованных коэффициентов смертности для проведения сравнений уровней смертности на самом деле вовсе не обязателен. Это, скорее всего, лишь дань привычке, уступка нашему желанию увидеть коэффициенты смертности в привычном виде. Однако эта привычка не безобидна, так как заставляет некоторых аналитиков трактовать величину стандартизованного коэффициента аналогично фактической. В этом случае нередко рассуждают так: «Фактические коэффициенты измеряют процесс неправильно, потому что их величина зависит от особенностей возрастной структуры. А стандартизованные коэффициенты (их величина) отражают уровень демографического процесса правильно, потому что они свободны от влияния возрастной структуры». Между тем величина стандартизованного коэффициента вовсе не характеризует уровень смертности. Сама по себе она — условна, самостоятельного значения не имеет никакого (ведь она во многом зависит от особенностей возрастной структуры стандарт-населения).
Поэтому вполне можно ограничиться расчетом индексов, выражающих соотношение фактических и условных чисел умерших, с последующим сравнением между собой уже этих индексов. Представим это рассуждение в виде формулы:
JmСТ
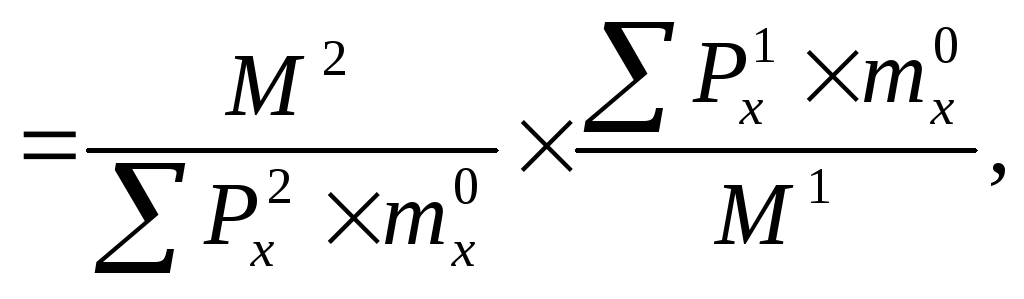 (6.9)
(6.9)
где все условные обозначения известны из предыдущей формулы. От подобного упрощения расчет станет только точнее (за счет сокращения количества округлений).
В качестве примера сравним уровни смертности мужского и женского населения России в 1995 г.1 (таблица 6.4). Общие коэффициенты смертности мужского и женского населения России в 1995 г. составили соответственно 16,9 и 13,3‰. Отсюда определяем, что уровень смертности мужчин выше, чем женщин, на 16,9/13,3 = 1,271, т.е. на 27,1%. Это немало, но с такой разницей можно было бы согласиться. Однако мы догадываемся, что именно в силу более высокой продолжительности жизни женщин по сравнению с мужчинами их возрастная структура в среднем старше аналогичной структуры мужского населения. Стандартизация коэффициентов смертности позволяет устранить (элиминировать) влияние различий возрастной структуры мужского и женского населения на величину общих коэффициентов смертности, так сказать, уравнять их в этом отношении. Окончательный расчет по формуле будет таким:
JmСТ = 1197048 / 779467 х 1428193 / 1055541 = 1,536 х 1,353 = 2,078
Результат расчета показывает, что на самом деле смертность мужчин выше, чем смертность женщин, не на 27%, а в 2,1 раза. Это уже явно ничем не оправданная и нетерпимая разница в продолжительности жизни, имеющая далеко идущие и многообразные демографические и другие социальные последствия.
В заключение этого раздела хочу обратить внимание на два очень важных обстоятельства, связанных с использованием методов стандартизации коэффициентов.
Во-первых, не существует какого-либо формализованного способа выбора (подбора) стандарт-населения. Это делается на основе опыта. Подбирается население — его параметры (возрастная структура при прямом методе стандартизации — или возрастные коэффициенты смертности — при косвенном методе), — о котором априори известно, что оно по этим параметрам схоже с теми населениями, уровни демографических процессов которых (любых, не обязательно только смертности) сравниваются между собой. Если сравниваются населения с резко различающимися возрастными структурами, то параметры стандарт-населения выбираются таким образом, чтобы они были средними между параметрами сравниваемых населений (предполагаемых или известных за другие годы и т.п.).
Таблица 6.4
Стандартизация общих коэффициентов смертности мужского и женского населения России в 1995 г. Косвенным методом
|
Возрастные группы (лет)
|
Численность населения на середину 1995 г. (тыс. человек) Рх
|
Возрастные коэффициенты смертности стандарт-населения в промилле mx0 |
Условное число умерших Рх х тх
|
||
|
Мужчины
|
Женщины
|
Мужчины
|
Женщины
|
||
|
0¾4 |
3892 |
3693 |
4,1 |
15957 |
15141 |
|
5—9 |
5856 |
5606 |
0,6 |
3514 |
3364 |
|
10—14 |
6059 |
5861 |
0,5 |
3030 |
2931 |
|
15—19 |
5525 |
5367 |
1,6 |
8840 |
8587 |
|
20—24 |
5275 |
5042 |
2,7 |
8440 |
8067 |
|
25—29 |
4896 |
4632 |
3,4 |
16646 |
15749 |
|
30—34 |
5728 |
5641 |
4,6 |
26349 |
25949 |
|
35—39 |
6396 |
6477 |
6,3 |
40295 |
40805 |
|
40¾44 |
5838 |
6081 |
8,9 |
51958 |
54121 |
|
45—49 |
4755 |
5134 |
12,3 |
58487 |
63148 |
|
50—54 |
2462 |
2888 |
17,1 |
42100 |
49385 |
|
55—59 |
4308 |
5460 |
21,4 |
92191 |
116844 |
|
60—64 |
2861 |
3965 |
29,7 |
84972 |
117761 |
|
65—69 |
2906 |
4764 |
39,2 |
113915 |
186749 |
|
70—74 |
1279 |
3298 |
51,3 |
65613 |
169187 |
|
75—79 |
600 |
1808 |
78,2 |
46920 |
141386 |
|
80—84 |
436 |
1629 |
123,2 |
53715 |
200693 |
|
85 и старше |
217 |
974 |
214,4 |
46525 |
208826 |
|
Всего |
69289 |
78320 |
15,0 |
779467 |
1428193 |
Во-вторых, считаю необходимым повторно предупредить читателя о том, что сама по себе величина стандартизованных коэффициентов носит условный характер, зависит от выбранного стандарта (стандарт-населения), поэтому она не имеет никакого самостоятельного значения. Имеет значение только разница между стандартизованными коэффициентами, которая в идеале остается неизменной при любом стандарте (небольшая разница в результатах может быть следствием грубости расчета, округлений цифр либо не очень удачного выбора стандарт-населения, если оно по своим характеристикам очень сильно отличается от сравниваемых населений).
6.5. Вероятностные таблицы смертности (чаще
называемые просто таблицами смертности)
Это самый совершенный инструмент для анализа состояния и тенденций уровня смертности. Они представляют собой систему взаимосвязанных показателей, характеризующих изменение вероятности смерти по мере увеличения возраста людей, или, напротив, изменение вероятности дожития до некоторого возраста, а также среднюю продолжительность жизни некоторого поколения родившихся. Иначе говоря, таблицы смертности описывают последовательность и скорость вымирания поколения.
Показатели (колонки) таблиц смертности:
lx — числа доживающих до возраста «х» лет;
dx — числа умирающих в возрасте «х» лет (т.е. в возрастном интервале от «х» до «х + 1»);
qx — вероятность умереть в возрасте «х» (т.е. в возрастном интервале от «х» до «х + 1»);
рх — вероятность для доживших до возраста «х» дожить и до следующего года возраста «х + 1»;
Lx — числа живущих в возрасте «x» (в возрастном интервале от «х» до «х + 1»;
Тх — числа живущих в возрасте «х» лет и старше (число человеко-лет предстоящей жизни для данного поколения);
е0 — средняя ожидаемая продолжительность жизни для новорожденных;
ех — средняя ожидаемая продолжительность жизни для достигших возраста «х».
В таблицах смертности принимают первоначальную численность поколения (число родившихся, основание или корень таблицы смертности) неизменной во времени и равной единице и прослеживают, как с переходом от возраста к возрасту, от 0 до предельного возраста (100 лет или 100 с небольшим) первоначальная совокупность поколения родившихся убывает в результате смерти от 1 до 0.