Файл: Методические указания по изучению дисциплины и выполнению контрольных работ для студентов заочной формы обучения направлений.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 128
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
4.
-
Y
X
2
7
12
17
22
27
nу
6
4
2
-
-
-
-
6
12
-
6
2
-
-
-
8
18
-
-
5
40
5
-
50
24
-
-
2
8
7
-
17
30
-
-
-
4
7
8
19
nx
4
8
9
52
19
8
n=100
5.
-
Y
X
11
16
21
26
31
36
nу
20
1
5
-
-
-
-
6
30
-
5
3
-
-
-
8
40
-
-
9
40
2
-
51
50
-
-
4
11
6
-
21
60
-
-
-
4
7
3
14
nx
1
10
16
55
15
3
n=100
6.
-
Y
X
2
7
12
17
22
27
nу
8
2
4
-
-
-
-
6
12
-
3
7
-
-
-
10
16
-
-
5
30
10
-
45
20
-
-
7
10
8
-
25
24
-
-
-
5
6
3
14
nx
2
7
19
45
24
3
n=100
7.
-
Y
X
11
16
21
26
31
36
nу
10
2
4
-
-
-
-
6
20
-
6
2
-
-
-
8
30
-
-
3
50
2
-
55
40
-
-
1
10
6
-
17
50
-
-
-
4
7
3
14
nx
2
10
6
64
15
3
n=100
8.
-
Y
X
4
9
14
19
24
29
nу
25
2
4
-
-
-
-
6
35
-
9
3
-
-
-
9
45
-
-
6
45
4
-
55
55
-
-
2
8
6
-
16
65
-
-
-
4
7
3
14
nx
2
10
11
57
17
3
n=100
9.
-
Y
X
5
10
15
20
25
30
nу
8
3
3
-
-
-
-
6
18
-
5
4
-
-
-
9
28
-
-
40
2
8
-
50
38
-
-
5
10
6
-
21
48
-
-
-
4
7
3
14
nx
3
8
49
16
21
3
n=100
10.
-
Y
X
2
7
12
17
22
27
nу
11
4
2
-
-
-
-
6
21
-
5
3
-
-
-
8
31
-
-
5
45
55
5
55
41
-
-
2
8
7
-
17
51
-
-
-
4
7
3
14
nx
2
10
11
57
17
3
n=100
7 Вопросы для подготовки к экзамену
7.1 Вопросы для подготовки к экзамену. Семестр 1
-
Определитель третьего порядка. -
Решение систем линейных уравнений по правилу Крамера. -
Определение скалярного произведения векторов. -
Понятие векторного произведения векторов, его приложения. -
Смешанное произведение векторов, его приложения. -
Уравнения прямой на плоскости. -
Плоскость в пространстве. -
Уравнения прямой в пространстве. -
Кривые второго порядка. -
Комплексных чисел и действий над ними. -
Нахождение модуля и аргумента комплексного числа. -
Тригонометрическая и показательная формы комплексного числа. -
Нахождение корней целой степени из комплексных чисел. -
Что называется пределом функции. -
Бесконечно малые и бесконечно большие функции. -
Раскрытие неопределенностей 0/0 и ∞/∞. -
Первый и второй замечательный пределы, их следствия. -
Дать определение непрерывности функции. -
Точки разрыва и их классификация. -
Производная функции, ее геометрический и физический смысл. -
Основные правила дифференцирования. -
Основные приложения производной. -
Промежутки монотонности и экстремумы функции. -
Необходимое и достаточное условия экстремума. -
Выпуклость и вогнутость, точки перегиба графика функции. -
Нахождение асимптот графика функции.
7.2 Вопросы для подготовки к экзамену. Семестр 2
-
Функции нескольких переменных, основные понятия и определения. -
Частные производные 1-го и 2-го порядков функции двух переменных. -
Дифференциалы 1-го и 2-го порядков функции двух переменных. -
Экстремумы функции двух переменных. -
Задачи, приводящие к дифференциальным уравнениям. -
Дифференциальные уравнения с разделяющимися переменными. -
Дифференциальные уравнения вида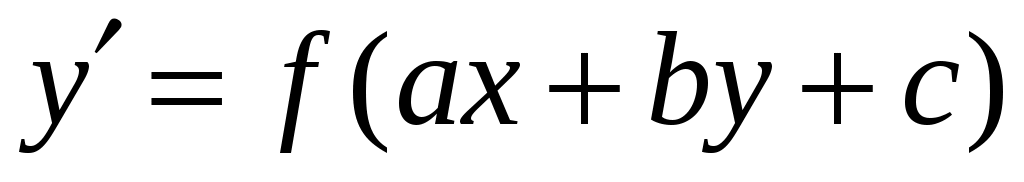 .
. -
Однородные дифференциальные уравнения первого порядка. -
Линейные дифференциальные уравнения 1-го порядка. Уравнение Бернулли. -
Уравнения старших порядков, допускающие понижение порядка. -
Линейно независимые и линейно зависимые системы функций. Определитель Вронского. Фундаментальная система решений (ФСР). -
Линейные однородные дифференциальные уравнения с постоянными коэффициентами. ФСР. -
Линейные дифференциальные уравнения с постоянными коэффициентами и специальной правой частью. -
Системы линейных дифференциальных уравнений 2-го порядка с постоянными коэффициентами. -
Бесконечные числовые ряды. Сходимость. Сумма числового ряда. -
Признаки сходимости знакопостоянных рядов. -
Абсолютно и не абсолютно сходящиеся ряды. Признак Лейбница. -
Функциональные ряды. Поточечная и равномерная сходимость. -
Непрерывность, интегрируемость и дифференцируемость суммы равномерно сходящихся рядов. -
Степенные ряды. Основные определения и теоремы. -
Ряды Тейлора и Маклорена. -
Вычисление значений функций и интегралов с помощью степенных рядов. -
Решений дифференциальных уравнений с помощью степенных рядов. -
Основные понятия теории вероятности. Случайные события. -
Вероятность случайных событий. Основные соотношения между вероятностями событий. -
Классическая вероятностная схема. Комбинаторный метод вычисления вероятностей в классической вероятностной схеме. -
Условные вероятности. Независимость случайных событий. -
Формула полной вероятности и формула Байеса. -
Повторные испытания. Формула Бернулли и формула Пуассона. -
Локальная и интегральная теоремы Лапласа-Муавра. -
Случайные величины. Функция распределения вероятностей. -
Дискретные случайные величины. Среднее значение и дисперсия. -
Непрерывные случайные величины. Среднее значение и дисперсия. -
Свойства среднего значения. Независимые случайные величины. -
Свойства дисперсии. Ковариация. Коэффициент регрессии. -
Распределение Бернулли. Распределение Пуассона. -
Равномерное распределение. Распределение Гаусса. Правило 3-х сигм. -
Выборка и ее представление. Полигон и Гистограмма. -
Числовые характеристики выборки. Выборочное среднее и выборочная дисперсия. Оценка параметров распределения по выборке.