Файл: Методические указания по изучению дисциплины и выполнению контрольных работ для студентов заочной формы обучения направлений.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 124
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
4.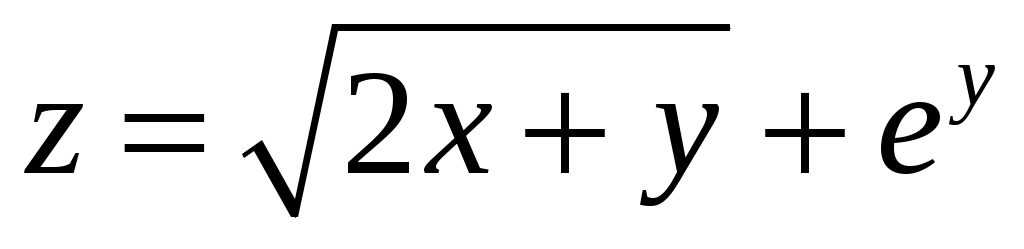 . 9.
. 9.  .
.
5.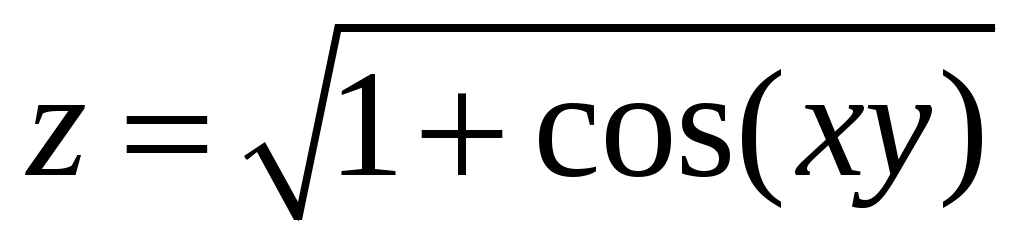 . 10.
. 10. 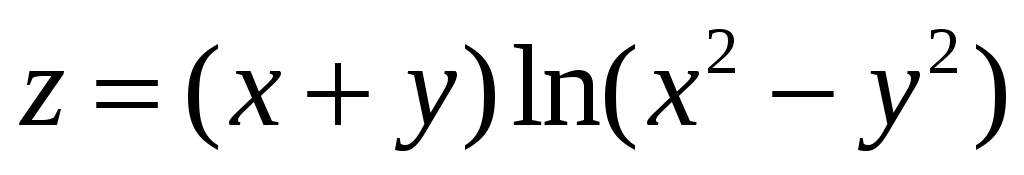 .
.
Задание № 7.
4. На пяти карточках написано по одной цифре из набора 1, 2, 3, 4, 5. Наугад выбирают одну за другой две карточки. Какова вероятность того, что число на второй карточке будет больше, чем на первой?
5. Из партии, в которой 20 деталей без дефектов и 5 с дефектами, берут наудачу 3 детали. Чему равна вероятность того,, что: 1) все три детали без дефектов; 2) по крайней мере одна деталь без дефектов?
6. Слово «карета», составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке Из коробки наугад извлекают буквы одну за другой. Какова вероятность получить при таком извлечении слово «ракета»?
7. Ящик содержит 10 деталей, среди которых 3 стандартных. Найти вероятность того, что из наудачу отобранных 5 деталей окажется не более одной стандартной
8. Брошены два одинаковых игральных кубика. Найти вероятность того,
что цифра 6 появится хотя бы на одной грани
Задание № 8.
Задание №9. Заданы математическое ожидание т и среднее квадратичное отклонение нормально распределенной случайной величины х. Найти:
1) вероятность того, что х примет значение, принадлежащее интервалу (, ).
2) вероятность того, что абсолютная величина отклонения окажется меньше .
окажется меньше .
Задание №10. Найти выборочное уравнение прямой регрессии Yна Xпо данной корреляционной таблице:
1.
2.
3.
4.
5.
Задание № 7.
-
Три стрелка стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75; для второго — 0,8; для третьего — 0,9. Найти вероятность того, что- 1) все три стрелка попадут в цель; 2) все трое промахнутся; 3) только один стрелок попадет в цель; 4) хотя бы один стрелок попадет в цель -
В первом ящике 6 белых и 4 черных шара, во втором — 7 белых и 3 черных. Из каждого ящика наугад вынимают по одному шару. Чему равна вероятность тощ, что вынутые шары разного цвета? -
На двух станках производятся одинаковые детали. Вероятность того, что деталь стандартная, для первого станка равна 0,8, для второго — 0,9. Производительность второго станка втрое больше, чем первого Найти вероятность того, что взятая наудачу деталь окажется стандартной.
4. На пяти карточках написано по одной цифре из набора 1, 2, 3, 4, 5. Наугад выбирают одну за другой две карточки. Какова вероятность того, что число на второй карточке будет больше, чем на первой?
5. Из партии, в которой 20 деталей без дефектов и 5 с дефектами, берут наудачу 3 детали. Чему равна вероятность того,, что: 1) все три детали без дефектов; 2) по крайней мере одна деталь без дефектов?
6. Слово «карета», составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке Из коробки наугад извлекают буквы одну за другой. Какова вероятность получить при таком извлечении слово «ракета»?
7. Ящик содержит 10 деталей, среди которых 3 стандартных. Найти вероятность того, что из наудачу отобранных 5 деталей окажется не более одной стандартной
8. Брошены два одинаковых игральных кубика. Найти вероятность того,
что цифра 6 появится хотя бы на одной грани
-
Для поражения цели достаточно попадания хотя бы одного снаряда. Произведено два залпа из двух орудий Найти вероятность поражения цели, если вероятность попадания в цель при одном выстреле из первого орудия равна 0,3, а из второго — 0,4 -
В урне лежит 12 белых и 8 красных шаров. Вынули 8 шаров. Какова вероятность того, что 1) три из них красные; 2) красных шаров вынуто не более трех
Задание № 8.
-
Вероятность появления события А при одном испытании равна 0,1. Найти вероятность того, что при трех независимых испытаниях оно появится 1) не менее двух раз, 2) хотя бы один раз. -
Игральную кость подбрасывают три раза. Найти вероятность того, что дважды появится число очков, кратное трем. -
Событие В появится в случае, если событие А появится не менее четырех раз Найти вероятность того, что наступит событие В, если будет произведено пять независимых испытаний, в каждом из которых вероятность появления события А равна 0,5. -
Случайно встреченное лицо может оказаться, с вероятностью р = 0,2,брюнетом, с р = 0,3 - блондином, с р=0,4 - шатеном и с р = 0.1 - рыжим. Какова вероятность того, что среди трех случайно встреченных лиц; 1) не менее двух брюнетов; 2) один блондин и два шатена; 3) хотя бы один рыжий? -
Вероятность хотя бы одного попадания при двух выстрелах равна 0,99. Найти вероятность трех попаданий при четырех выстрелах. -
В квартире четыре электролампочки. Для каждой лампочки вероятность того, что она останется неисправной в течение года, равна 5/6. Какова вероятность того, что в течение года придется заменить не менее половины лампочек? -
В ящике имеется по одинаковому числу деталей, изготовленных заводами № 1 и № 2. Найти вероятность того, что среди пяти наудачу отобранных деталей, изготовлены заводом № 1: 1) две детали; 2) менее двух деталей; 3) более двух деталей. -
Пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из трех телевизоров: 1) не более одного потребует ремонта: 2) хотя бы один «е потребует ремонта. -
В ящике лежат несколько тысяч одинаковых предохранителей. Половина из них изготовлена I заводом, остальные - II заводом. Наудачу вынули пять предохранителей. Чему равна вероятность того, что I заводом из них изготовлены: 1) два предохранителя; 2) менее двух предохранителей; 3) более двух предохранителей? -
Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие не стандартно, равна 0,1. Найти вероятность того, что: 1) из трех проверенных изделий только одно нестандартное; 2) нестандартным будет только третье по порядку проверенное изделие. -
Игральную кость подбрасывают 500 раз. Какова вероятность того, что цифра 1 при этом выпадет 50 раз? -
Вероятность получения по лотерее без выигрышного билета равна 0,1. Какова вероятность того, что среди 400 наугад купленных билетов не менее 50 и не более 60 без выигрышных? -
Чему равна вероятность того, что среди 100 случайных прохожих окажутся 32 женщины (предполагается, что число мужчин и женщин в городе одинаково)? -
Вероятность наступления события А в каждом из 100 независимых испытаний равна 0,8. Найти вероятность того, что событие А появится в этих испытаниях- 1) равно 90 раз; 2) не менее 80 и не более 90 раз -
Вероятность выздоровления больного в результате применения нового способа лечения равна 0,8 Сколько вылечившихся из 100 больных можно ожидать с вероятностью 0,75? -
Игральную кость подбрасывают 320 раз. Какова вероятность того, что цифра 5 при этом выпадет не менее 70 и не более 83 раз? -
Вероятность того, что пассажир опоздает к отправлению поезда, равна 0,02. Найти наиболее вероятное число опоздавших из. 625 пассажиров и вероятность этого события. -
При проведении эксперимента монету подбрасывали 4096 раз, причем герб выпал 2068 раз. С какой вероятностью можно было ожидать этот результат? -
Найти вероятность того, что в партии из 900 изделий число изделий высшего сорта заключено между 600 и 700. Вероятность появления изделия высшего сорта в партии равна 0,8. -
Игральный кубик подбросили 125 раз. Какова вероятность того, что цифра 6 появилась не более 60 раз?
Задание №9. Заданы математическое ожидание т и среднее квадратичное отклонение нормально распределенной случайной величины х. Найти:
1) вероятность того, что х примет значение, принадлежащее интервалу (, ).
2) вероятность того, что абсолютная величина отклонения
-
m =15, = 2, =16, = 25, = 4. -
m =14, = 4, =18, = 34, = 8. -
m =13, = 4, =15, = 17, = 6. -
m =12, = 5, =17, = 22 = 15. -
m =11, = 3, =17, = 26, = 12. -
m =10, = 2, =11, = 13, = 5. -
m = 9, = 4, =15, = 19, =18. -
m = 8, = 2, = 6, = 15, = 8. -
m = 7, = 5, = 2, = 22, = 20. -
m = 6, = 3, = 0, = 9, = 9.
Задание №10. Найти выборочное уравнение прямой регрессии Yна Xпо данной корреляционной таблице:
1.
-
Y
X
5
10
15
20
25
30
nу
10
2
3
-
-
-
-
5
20
-
7
3
-
-
-
10
30
-
-
2
50
2
-
54
40
-
1
10
6
-
17
50
-
-
-
4
7
3
14
nх
2
10
6
64
15
3
n=100
2.
-
Y
X
15
20
25
30
35
40
nу
30
2
6
-
-
-
-
8
40
-
4
4
-
-
-
8
50
-
-
7
35
8
-
50
60
-
-
2
10
8
-
20
70
-
-
-
5
6
3
14
nx
2
10
13
50
22
3
n=100
3.
-
Y
X
4
9
14
19
24
29
nу
5
4
2
-
-
-
-
6
10
-
6
4
-
-
-
10
15
-
-
6
45
2
-
53
20
-
-
2
8
6
-
16
25
-
-
-
4
7
4
15
nx
4
8
12
57
15
4
n=100