Тема 6. Дифференциальные уравнения.

Общие сведения о дифференциальных уравнениях. Задачи, приво­дящие к дифференциальным уравнениям. Дифференциальные уравнения 1-го порядка: с разделяющимися переменными, однородные, линейные, уравнение Бернулли. Дифференциальные уравнения высших порядков: допускающие по­нижение порядка. Линейные однородные ДУ второго порядка. Структура общего решения. Линейные однородные ДУ второго порядка с постоянными коэффициентами. Линейные неоднородные ДУ второго порядка с постоянными коэффициентами.

Литература: [2, гл. 13, §§2-8,16,20,21], [4, гл. 15, §§1-4].

Вопросы для самоконтроля

5. 
   Определение дифференциального уравнения и его порядка.
   
6. 
   Решение (общее и частное) дифференциального уравнения.
   
7. 
   Дифференциальное уравнение с разделяющимися переменными.
   
8. 
   Линейные дифференциальные уравнения 1-го порядка. Метод Бернулли.
   
9. 
   Дифференциальные уравнения высших порядков: допускающие пониже­ние порядка.
   

Тема 7. Числовые и функциональные ряды.

Числовые ряды, их сходимость. Основные понятия и свойства. Необ­ходимые условия сходимости. Остаток ряда. Свойства сходящихся рядов. Знакоположительные ряды. Признаки сравнения. Достаточные признаки Даламбера, Коши, интегральный признак Коши. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов. Функциональные ряды. Сходимость в точке, радиус сходимости и область сходимости. Степенные ряды. Теорема Абеля. Радиус сходимости и его вычисление. Интервал и область сходимости степенного ряда.

Литература: [4, гл. 14, §§1-5], [6, ч.2, гл. III, §§1-4].

Вопросы для самоконтроля

1. 
   Определение числового ряда, общий член ряда, n-я частичная сумма.
   
2. 
   Сходящиеся и расходящиеся числовые ряды.
   
3. 
   Необходимый признак сходимости.
   
4. 
   Признаки сравнения (I и II).
   
5. 
   Признаки Даламбера и Коши (радикальный, интегральный).
   
6. 
   Знакочередующийся ряд. Признак Лейбница.
   
7. 
   Абсолютная и условная сходимость.
   
8. 
   Степенной ряд. Интервал сходимости. Область сходимости.
   

Тема 8. Теория вероятностей и математическая статистика.

Основные понятия теории вероятностей. Случайные события и опера­ции над ними. Полная группа случайных событий. Классификация опреде­ления вероятности. Комбинаторика. Свойства вероятностей. Теорема сложения. Статистическое определение вероятности. Условная вероятность. Теорема умножения. Формула полной вероятности. Формула Байеса. Схема Бернулли повторных испытаний, наивероятнейшее число появ­лений событий. Локальная и интегральная предельные теоремы и их при­менение. Случайные величины. Законы распределения дискретных случайных величин. Функция распределения непрерывной случайной величины, ее свойства, плотность вероятности и ее свойства. Нормальный закон распре­деления и его применение. Математическое ожидание и его свойства. Дисперсия, ее свойства. Выборка и ее графическое представление. Выборочное среднее и дис­персия. Оценка параметров распределения по выборке.

---

Литература: [7, гл.1: §§1-5, гл.2 : §§1-3, гл.3: §§1-5, гл.4: §§1-3, гл.5 §1, гл.6: §§1,2, гл.7: §§1,2]; [8, гл.1 §1, гл.2 §§1-4, гл.3 §1, гл.4 §§1,3].

Вопросы для самоконтроля

1. 
   Классическое определение вероятности случайного события.
   
2. 
   Теорема сложения. Условная вероятность. Теорема умножения.
   
3. 
   Формула полной вероятности. Формула Байеса.
   
4. 
   Формула Бернулли. Наивероятнейшее число появлений.
   
5. 
   Закон распределения дискретной случайной величины.
   
6. 
   Математическое ожидание и дисперсия. Их свойства.
   
7. 
   Выборка. Выборочное среднее и дисперсия.
   

---

3 Контрольные работы

3.1 Контрольная работа №1. Семестр 1

Программой дисциплины «Математика» для студентов I курса в первом семестре предусмотрено выполнение одной контрольной работы.

При выполнении контрольной работы необходимо изучить элементы линейной и векторной алгебры, аналитической геометрии на плоскости и в пространстве, а также ознакомиться с теорией кривых второго порядка и комплексными числами. Необходимо научиться вычислять основные типы пределов – неопределенности , первый и второй замечательный пределы. Изучить понятие непрерывности функции, основы дифференциального исчисления функции одной переменной, а также их приложения к исследованию функции.

Ниже приведены примеры выполнения заданий.

Задание №1. Доказать, что векторы линейно независимы и найти разложение вектора по векторам , если , , , .

Решение. Покажем, что векторы - некомпланарны. Для этого найдем их смешанное произведение:

.

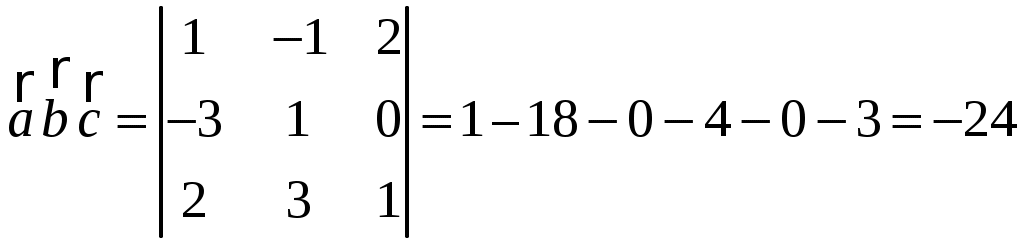Так как смешанное произведение отлично от нуля, то векторы линейно независимы. Найдем разложение вектора по векторам , т.е. , где

---

- неизвестные величины. Для нахождения этих величин составим систему трех линейных алгебраических уравнений:

; ;

.

Решим эту систему методом Гаусса. Первое уравнение оставим без изменения, для получения второго сложим два первых уравнения, а третье уравнение сложим с первым, умноженным на :



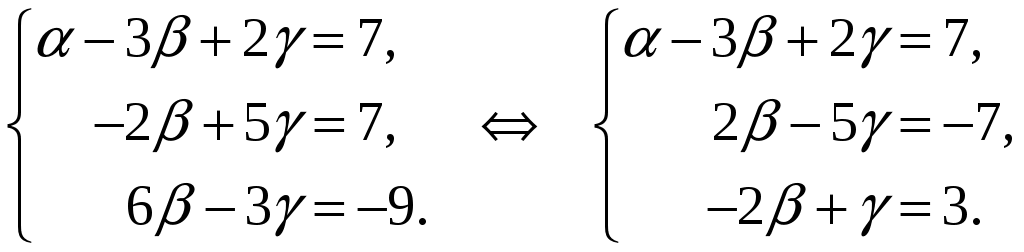
Первые два уравнения последней системы оставим без изменения, а третье сложим со вторым:



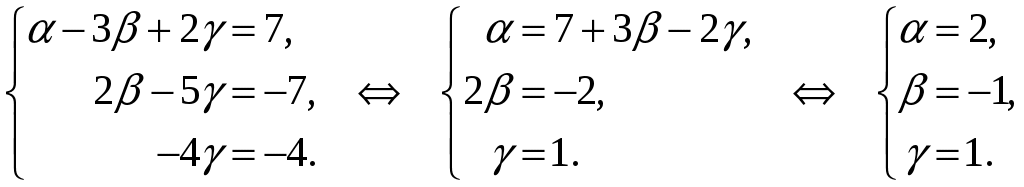
Таким образом, .

Задание №2. По координатам вершины пирамиды А₁А₂А₃А₄ найти:

1. 
   длину ребра А₁А₂;
   
2. 
   угол между ребрами А₁А₂ и А₁А₄;
   
3. 
   площадь грани А₁А₂А₃;
   
4. 
   объем пирамиды;
   
5. 
   уравнения плоскостей А₁А₂А₃ и А₁А₂А₄ ;
   
6. 
   угол между плоскостями А₁А₂А₃ и А₁А₂А₄.
   

1) Если заданы точки A₁(x₁, y₁, z₁),А₂(x₂,y₂,z₂), то координаты вектора равны , тогда длина вектора вычисляется по формуле .

2) Из определения скалярного произведения следует, что угол между векторами вычисляется по формуле

.

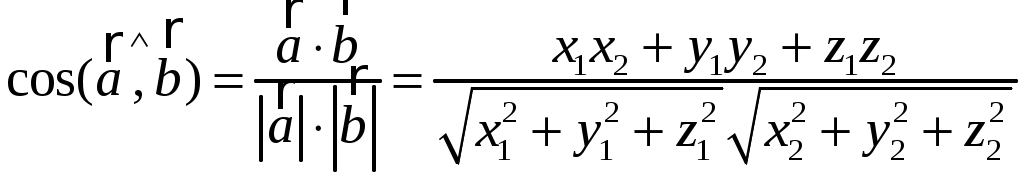3) - площадь треугольника, построенного на векторах

---

и .

4) Учитывая геометрический смысл смешанного произведения векторов, получим формулу вычисления объема пирамиды: .

5) Если даны три точки А₁(x₁; y₁; z₁), А₂(x₂; y₂; z₂) и А₃(x₃; y₃; z₃), то уравнение плоскости, проходящей через три точки, находится по формуле

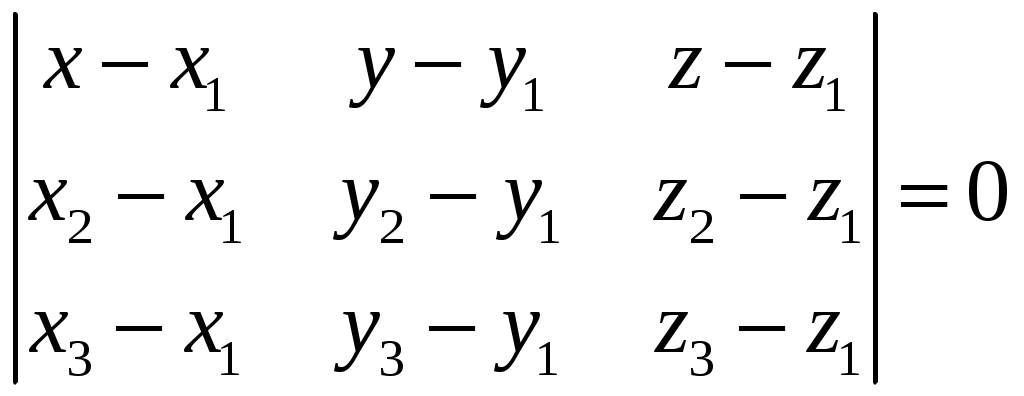. (1)

Например, составить уравнение плоскости, проходящей через три точки А₁, А₂ ,А₃, если А₁(-3, 2, 0), А₂(-2, 0, 2), А₃(0, 3, -1).

Решение: по формуле (1) получим ,



.

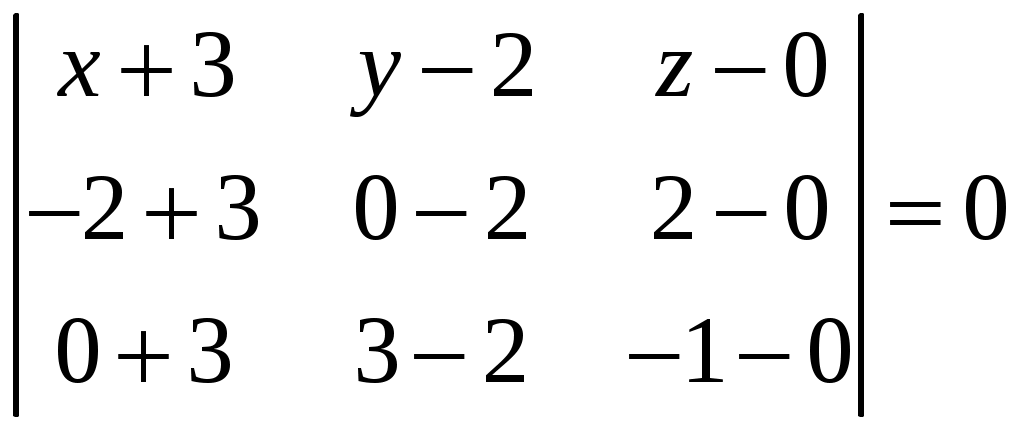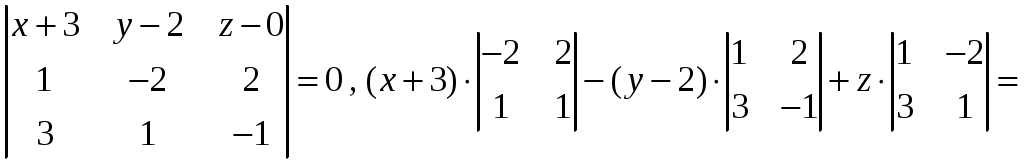
Итак, уравнение плоскости имеет вид , где нормаль имеет координаты .

6) Угол, образованный двумя плоскостями, находится по формуле

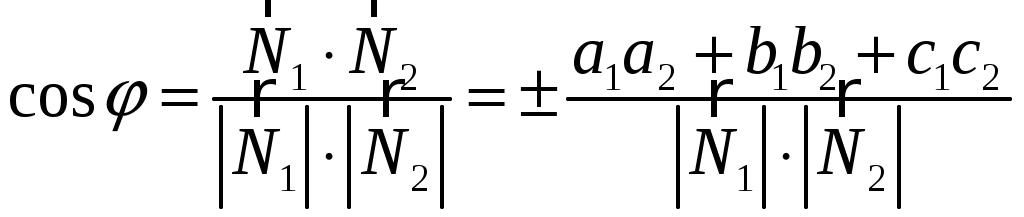, где и ‑ нормали плоскостей.

Задание №3. Найти уравнение данной кривой в декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью: .

Решение. Связь между полярными и прямоугольными координатами точки устанавливаются формулам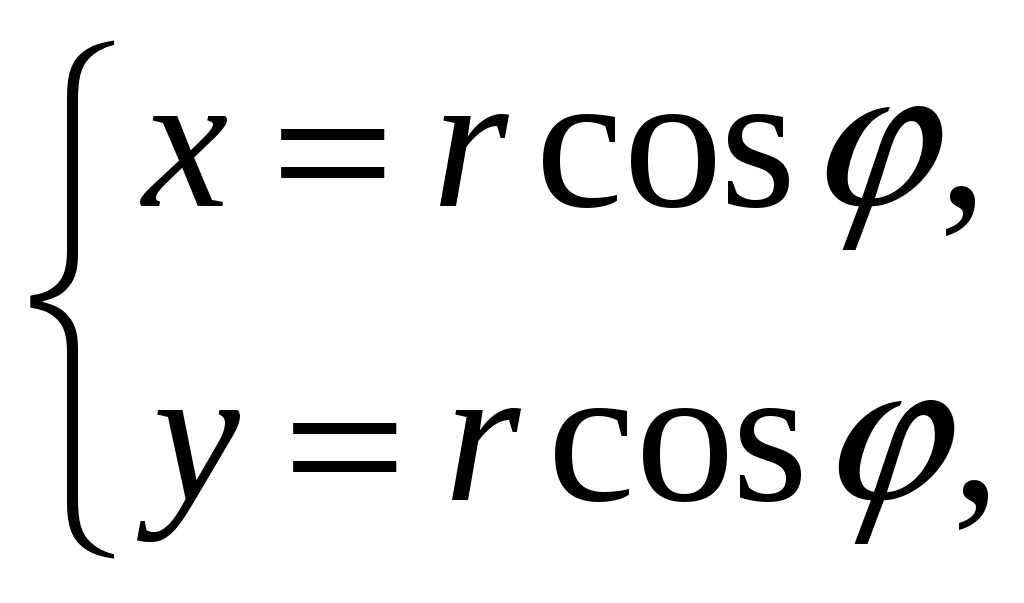и: и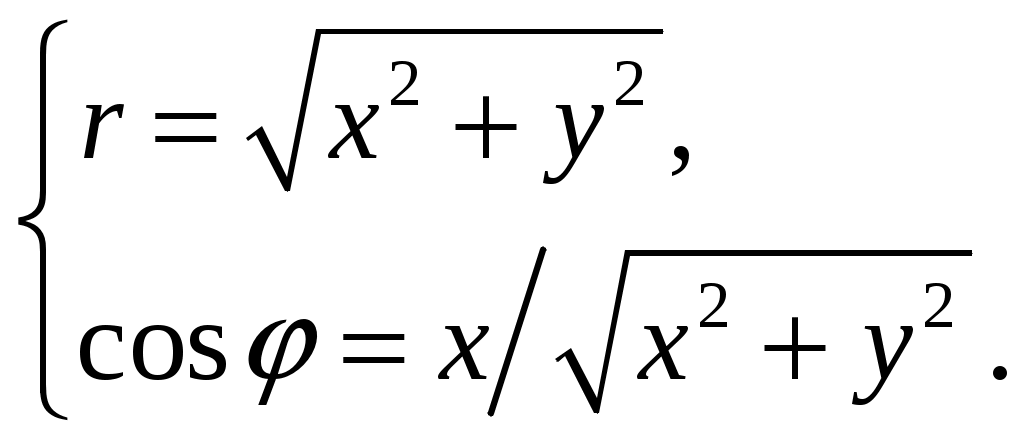



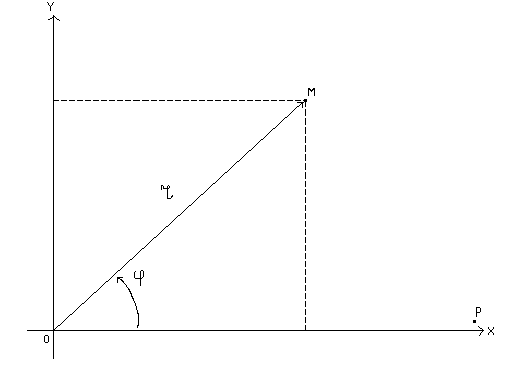
По условию

---

Смотрите также файлы

• Программа среднего профессионального образования 40.docx

• Гудалина Татьяна Анатольевна (И. О. Фамилия) Тольятти 2023 Практическое занятие.docx

• М. Т. Лукьянова понятие занятости и содействие в обеспечении занятости и трудоустройства, правовой статус безработного doi 10. 31563230896442022442132141 Ключевые слова занятость безработица трудоустройство э.pdf

• 1. Выбор материала 4.docx

• Назовите основные положения реформы Сервия Туллия. Как она повлияла на развитие Древнего Рима.docx