Файл: Министерство образования и науки рф московский государственный университет технологий и управления имени К. Г. Разумовского.doc

Математическая формулировка задачи оптимального ассортимента такова: определить значения неизвестных x₁, х₂, х₃ удовлетворяющие ограничениям, выраженным системой неравенств и равенств и обеспечивающие максимальное значение целевой функции, выраженной уравнением для определения ограничительных ресурсов.

Таблица 4

Виды основных ресурсов	Расход ресурсов на 1т продукции, т			Наличие ресурсов, т
	П1	П2	П3
P1	0,3	0,4	0,1	200
P2	0,2	0,1	0,3	303
Р3	0,4	0,3	0,1	270
Прибыль на 1т, руб.	1200	1400	1000

Предприятие располагает определенным количеством ресурсов (P₁, P₂, Р₃), общий расход которых на производство трех видов продукции не должен превышать заданных величин:

0,3x₁ + 0,4x₂ + 0,1x₃< 200

0,2x₁ + 0,1х₂ + 0,3х_з < 303

0,4x₁ + 0,3x₂ + 0,1x₃< 270

Выпуск продукции не может быть отрицательным, поэтому

х₁ ≥ 0, х₂ ≥ 0, х₃ ≥ 0.

Общая сумма прибыли (целевая функция)

F = 1200х₁ + 1400х₂ + 1000х

---

₃ = max.
Для решения задачи симплексным методом неравенства преобра­зуются в эквивалентные равенства путем добавления в каждое нера­венство по одному дополнительному неизвестному с коэффициентом + 1 и нулевым уравнением прибыли. Для удобства расчетов левые и правые части уравнений меняются местами. В этом случае исходные неравенства примут вид симплексных уравнений:



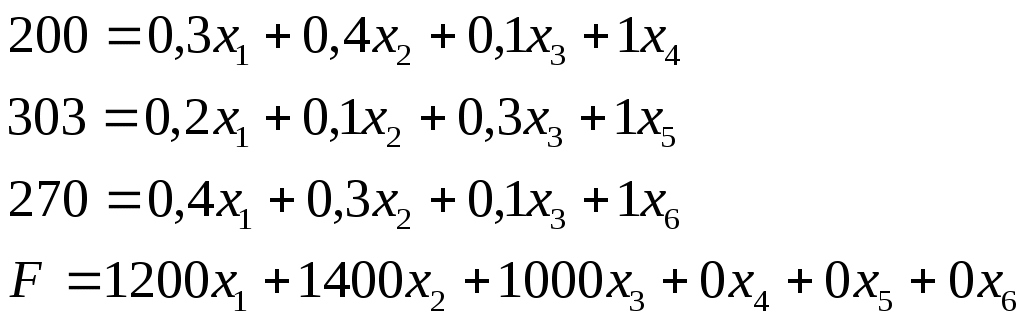
Коэффициенты при неизвестных записываются в симплексной таблице, в которой выполняются расчеты и отражаются полученные результаты.

В столбцах таблицы записывают: в первом (С_j) - прибыль единицы продукции, которая вводится в план выпуска; во втором (p₀) – неизвестные, включаемые в план; в третьем (х₀) – свободные величины; в остальных - коэффициенты при неизвестных уравнениях. В верхней части этих столбцов отражаются коэффициенты при неизвестных целевой функции.
Исходная таблица

сj	p0	x0	1200	1400	1000	0	0	0
			x1	x2	x3	x4	x5	x6
0	x4	200	0,3	0,4	0,1	1	0	0
0	x5	303	0,2	0,1	0,3	0	1	0
0	x6	270	0,4	0,3	0,1	0	0	1
Zj - Cj		0	-1200	-1400	-1000	0	0	0

В нижней строке (целевой) записываются получаемые расчетным путем показатели: в столбце х₀ - суммарная прибыль планового выпуска, в остальных столбцах - прибыль единицы продукции с отрицательным знаком.

---

В последних трех столбцах коэффициенты при дополнительных неизвестных, равные единице, расположены по диагонали. Эта часть таблицы, называемая единичной подматрицей, необходима для вычислительных и аналитических целей.

При решении задач на максимум целевой функции наличие в целевой строке отрицательных чисел указывает на возможность начала или продолжения решения задачи. Порядок решения таков: из отрицательных чисел целевой строки выбирается наибольшее по модулю. Столбец, в котором оно находится, принимается за ключевой (или разрешающий) и для удобства расчетов выделяется. В нашем примере таким столбцом будет x₂, имеющий в целевой строке наибольшую по модулю величину - 1400.

Затем элементы столбца x₀ (свободные величины) делят на соответствующие коэффициенты ключевого столбца и полученные результаты сопоставляют между собой. Строка с наименьшим отно­шением принимается за ключевую и также для удобства выделяется. В нашем случае 200/0,4 = 500, 303/0,1= 3030, 270/0,3 = 900. Наимень­шее отношение 500 имеет строка х₄, она и будет ключевой. Ключевой элемент 0,4.

Далее элементы таблицы преобразуются и записываются в новую таблицу (1-я итерация). Первоначально преобразуют элементы ключевой строки путем деления их на ключевой элемент. Преобразованные элементы записывают в том же самом месте:

200/0,4 = 500; 0,3/0,4 = 0,75; 0,4/0,4 =1; 0,1/0,4 = 0,25; 1/0,4 = 2,5

В столбцах Р₀ и С_j занимают место вводимая в план неиз­вестная x₂ с прибылью 1400 (1-я итерация). Остальные элемен­ты преобразуются по следующему правилу:

• 
  для преобразуемого элемента в его столбце находят элемент ключевой строки, а в его строке - элемент ключевого столбца;
  

- соответствующие элементы ключевой строки и ключевого столбца перемножаются и полученное произведение делят на ключевой момент;

- частное от деления вычитают из значения элемента, кото­рое он имел до преобразования, и полученный результат будет преобразованным элементом, который записывается в новую таблицу в том же самом месте.

Следуя этому правилу, преобразование элементов столбца х₀ будет:
303 -

270 -

---

0 -
Остальные элементы таблицы вычисляются также по вышеизложенному правилу:

2-я строка – x₅ :


Включение на первой итерации в план неизвестной х₂ (выпуск продукции П₂ вида) обеспечит сумму прибыли 700000 руб.
1-я итерация

сj	p2	x0	x1	x2	x3	x4	x5	x6
1400	x2	500	0,75	1	0,25	2,5	0	0
0	x5	253	0,125	0	0,275	-0,25	1	0
0	x6	120	0,175	0	0,125	-0,75	0	1
Zj - Cj		700000	-150	0	-650	3500	0	0

Решение задачи продолжается, так как в целевой строке два отрицательных элемента. Наибольший по модулю элемент - 650. Он находится в столбце x₃, который принимается за ключевой, а ключевой строкой будет x₅

(500 : 0,25 =2000; 253 : 0,275 = 920; 120 : 0,125 = 960). Элементы таблицы преобразуются в том же порядке по изложенному правилу и записываются в новую таблицу (2-я итерация).
2-я итерация

сj	p2	x0	x1	x2	x3	x4	x5	x6
49	x2	270	0,636	1	0	2,727	-0,91	0
9	x3	920	0,455	0	1	-0,001	3,636	0
28	x6	5	0,118	0	0	-0,636	-0,456	1
Zj - Cj		1298000	145,45	0	0	2909,1	2363,63	0

---

В последней таблице целевая строка имеет только положительные элементы. Это значит, что составленный план оптимален и дальнейшее улучшение его невозможно.

Как видно из таблицы, оптимальный план предусматривает выпуск продукции вида П₂ – 270 т (х₂ = 270), вида П₃ – 920 т (х₃ = 920), выпуск продукции вида П₁ производить не надо (х₁ = 0),. Дополнительные неизвестные (остатки сырья на складе) х₄ = 0, х₅ = 0, на складе осталось сырье третьего вида х₆= 5. Подставив значения неизвестных в уравнения, получим:

0,3*0 + 0,4*270 + 0,1*920 + 0 = 200

0,2*0 + 0,1*270 + 0,3*920 + 0 = 303

0,4*0 + 0,3*270 + 0,1*920 + 5 = 270
F = 1200*0 + 1400*270 + 1000*920 = 1298000

При постановке задачи были приняты ограничения только по запасам сырья (P₁, P₂, Р₃). Другие ограничения не учитывались. Но если бы в плане требовалось предусмотреть ассортиментные соотношения (например, выпуск продукции трех видов не должен превышать 1200 т, выпуск продукции вида П₂ должен быть не больше 400 т, а выпуск продукции вида П₃ должен быть не меньше 500 т, то в систему неравенств добавляются эти ограничения:







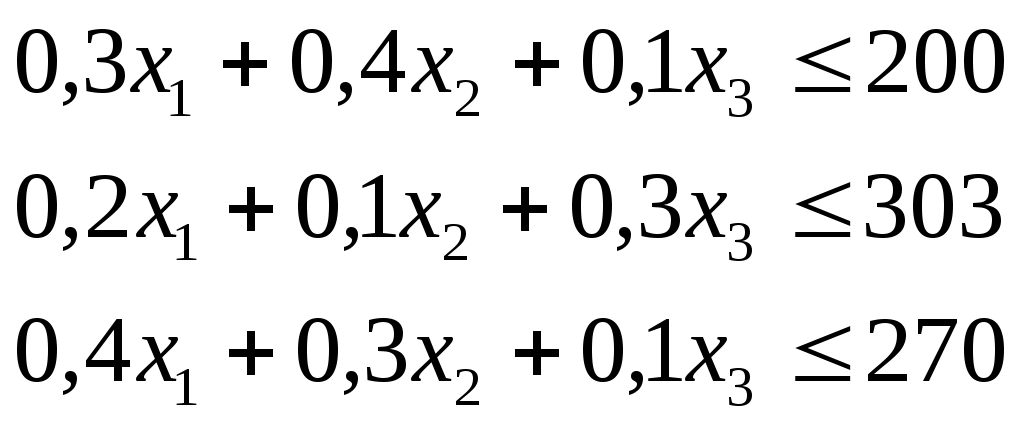
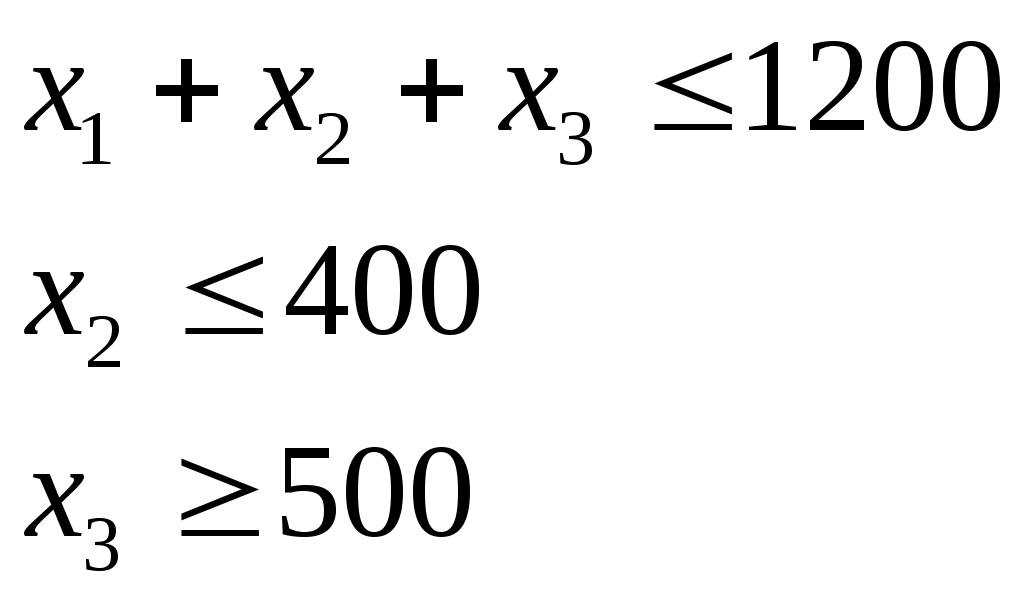
Эта система преобразуется в симплексные уравнения и решается по изложенным правилам.

Проведем анализ оптимального плана.

1) Запасы сырья первого и второго вида используются полностью без остатка, так как х₄ = х₅ = 0, на складе останется сырья третьего вида – 5 т (х₆ = 5).

2) Рассмотрим элементы матрицы.

Элементы столбца х₄ свидетельствуют: если запасы P₁ будут увеличены на I ед. (200 + 1), то выпуск продукции П₂ вида увели­чится на 2,727 ед. (х₂ = 270 + 2,727), выпуск продукции П₃ вида уменьшится на 0,001 ед. (920 – 0,001) на складе сырья третьего вида уменьшится на 0,636 т (х₆ = 5- 0,636). Сумма прибыли увеличится на 2909,1 руб.

Элементы столбца х₅ показывают, что увеличение запасов P₂ на I ед. (303 + 1) позволит увеличить выпуск продукции П₃ вида на 3,636 ед., уменьшится выпуск продукции П₂ вида на 0,91ед., прибыль увеличится на 2363,63 руб. Изменения объемов производства и суммы прибыли вызовет и уменьшение запасов Р₃ (х₆). Снижение запасов сырья приводит к изменениям выпуска продукции и суммы прибыли в обратном порядке.

---