Файл: Задача Геометрические характеристики плоских сечений.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Решение задач

Дисциплина: Не указана

Добавлен: 08.11.2023

Просмотров: 74

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Задача 1. Геометрические характеристики плоских сечений
Условие и порядок выполнения работы


  1. Вычертить в масштабе заданное поперечное сечение балки, провести вспомогательные оси. Выписать из ГОСТов требуемые величины и размеры, привязав их к центральным осям каждой фигуры чертежа. Проставить основные размеры.

  2. Определить положение центра тяжести всей фигуры, применив для этого статические моменты плоских фигур. Провести на чертеже через найденный центр тяжести параллельно прежним осям центральные оси всей фигуры.

  3. Найти осевые моменты инерции и центробежный момент инерции всей фигуры относительно её центральных осей.

  4. Определить моменты сопротивления фигуры относительно этих центральных осей.

  5. Найти положение главных центральных осей фигуры и провести их на чертеже. На чертеже показать угол поворота главных центральных осей инерции по отношению к прежним осям и его направление.

  6. Найти моменты сопротивления фигуры относительно главных центральных осей инерции. При этом расстояние от осей до наиболее удалённых точек фигуры допускается определять графически.

  7. Определить радиусы инерции фигуры относительно главных центральных осей и по ним построить эллипс инерции.

  8. Произвести проверку расчётов.


Исходные данные: швеллер 18а ГОСТ 8240-97, уголок равнополочный 100х100х12 ГОСТ 8509-93

Профиль балки:



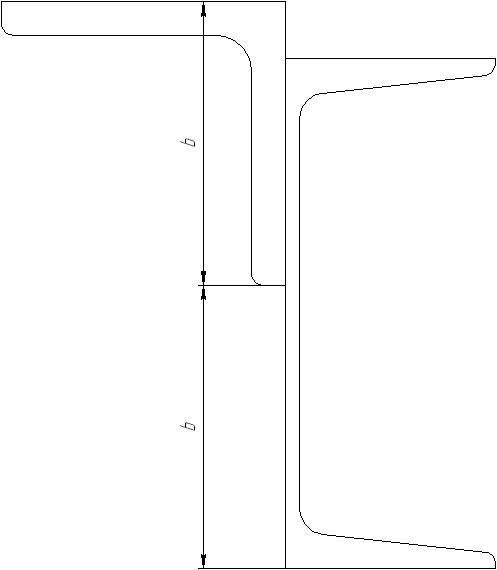
Дано:

Уголок. В=10 см, х =y =2,91 см; I =208,9 см ; I =122 см ; А=22,8 см

Швеллер. h=18 см; В=7,4 см; х
=2,13 см; I =1190 см ; I =105 см ; А=22,2 см .

Решение.
1. Определение координат центра тяжести всей сложной фигуры (положение центральных осей)
Х = = = =9,58 см;
Y = = = =13,06 см
где х , х , у , у - расстояние от центра тяжести каждого сечения до вспомогательных осей.
2. Определение осевых моментов инерции относительно центральных осей X , Y

I = I + I +а А +а А
;

I = I + I +b А +b А ,
где а , а , b , b - расстояние от центра тяжести каждого сечения до центральных осей.

Откладываем а по оси y,

b по оси х:
а =у -у =13,06-17,09=-4,03 см;

а =у -у =13,06-9=4,06 см;

b = х -х =9,58-7,09=2,49 см;

b =х -х =9,58-12,13=-2,55 см.
I =208,9+1190+(-4,03) ∙22,8+4,06 ∙22,2=2135,1 см
;

I =208,9+ 105+2,49 ∙22,8+(-2,55) ∙22,2=599,6 см .
3. Определение центробежного момента инерции относительно центральных осей Х и Y :
I = I + I +a b А + a b А ,
I =0, т.к. швеллер имеет горизонтальную ось симметрии, то собственные центральные оси швеллера являются главными;

I = 122+ 0+(-4,03)∙2,49∙22,8+4,06∙(-2,55)∙22,2=-336,6 см .
4. Определение моментов сопротивления относительно центральных осей Х и Y :
W = ; W = ,
где Х
, Y - максимальные расстояния от центра тяжести всей фигуры до наиболее удалённых точек по центральным осям;

Х = Х =9,58 см;

Y = Y =13,06 см.
W = =163,5 см ;

W = =62,6 см .
5. Определение положения главных центральных осей (U,V) и угла наклона (α):
tg2α=- =- =0,4384
α=11,8°, угол откладывается против часовой стрелке.
6. Определение главных центральных моментов инерции относительно главных центральных осей:
I = ±
I = + =

= + =2205,6 см

Смотрите также файлы