Файл: Задача Геометрические характеристики плоских сечений.doc
Добавлен: 08.11.2023
Просмотров: 78
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
+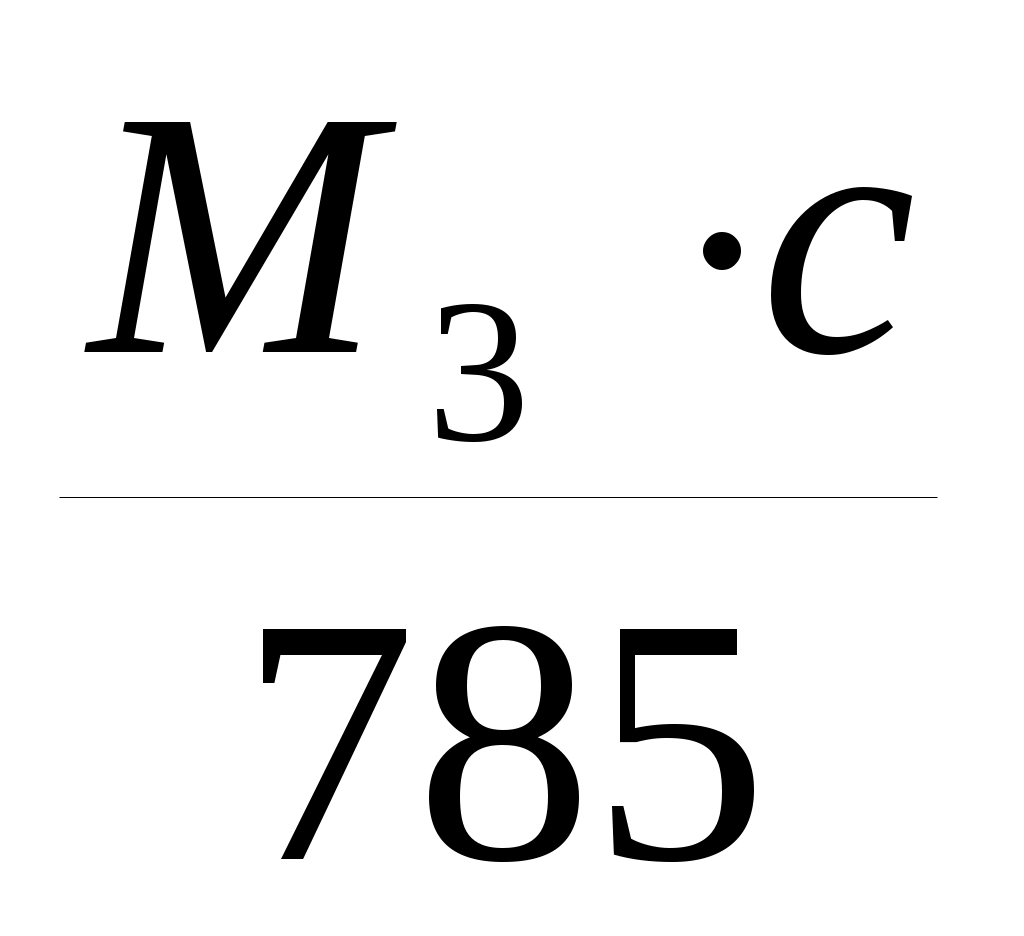 =-0,0088+
=-0,0088+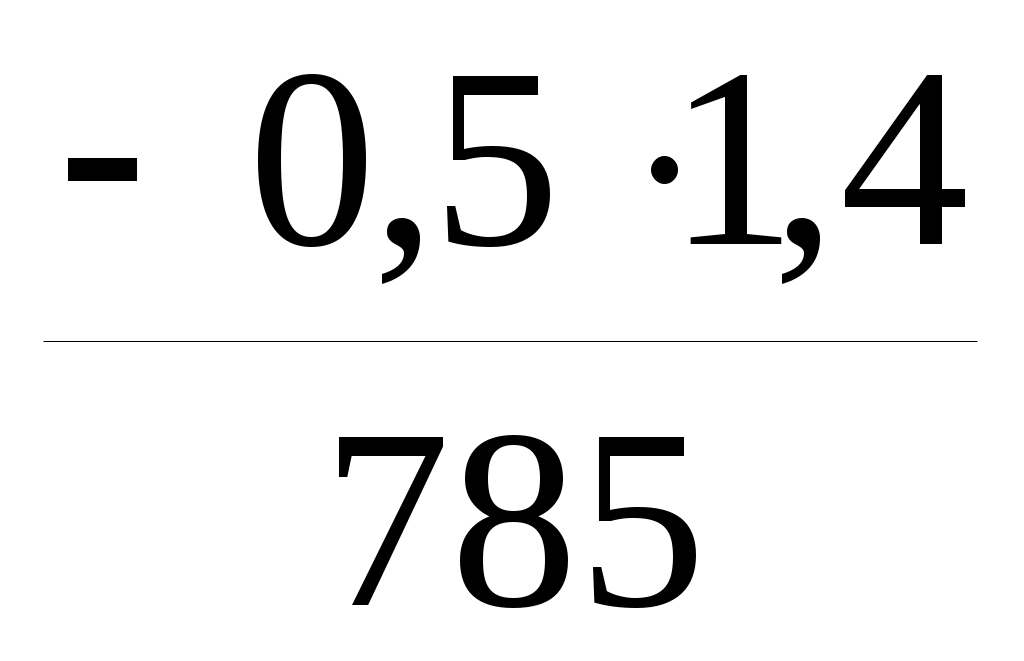 =-0,0097 рад;
=-0,0097 рад;
φ = φ
= φ +
+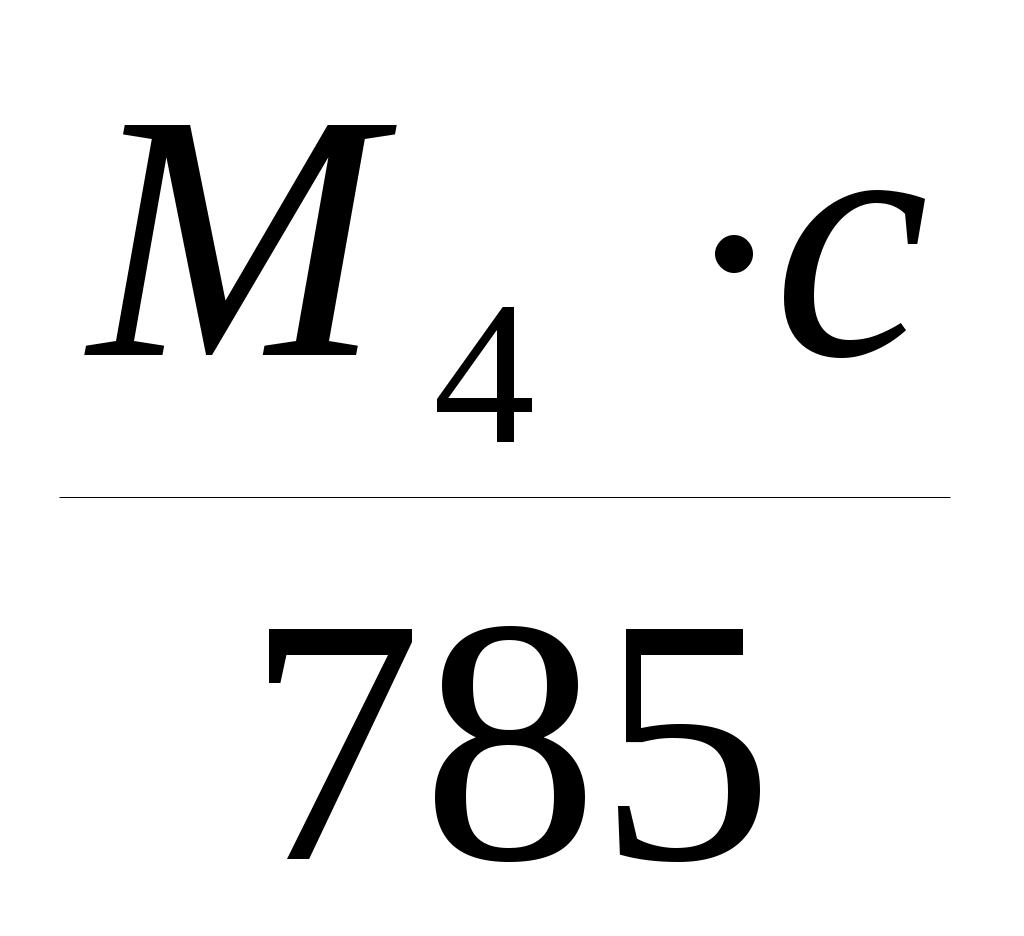 =-0,0097+
=-0,0097+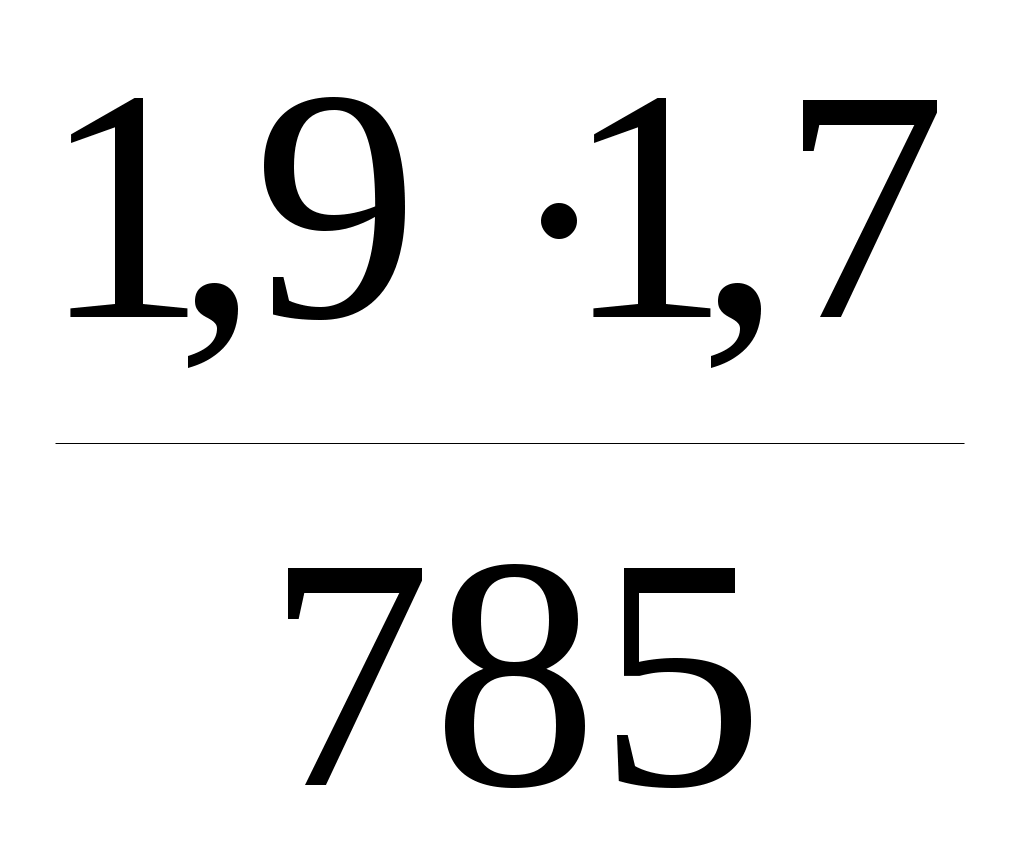 =-0,0076 рад.
=-0,0076 рад.
5. Определение относительного угла закручивания, возникающего на валу;
φ =
=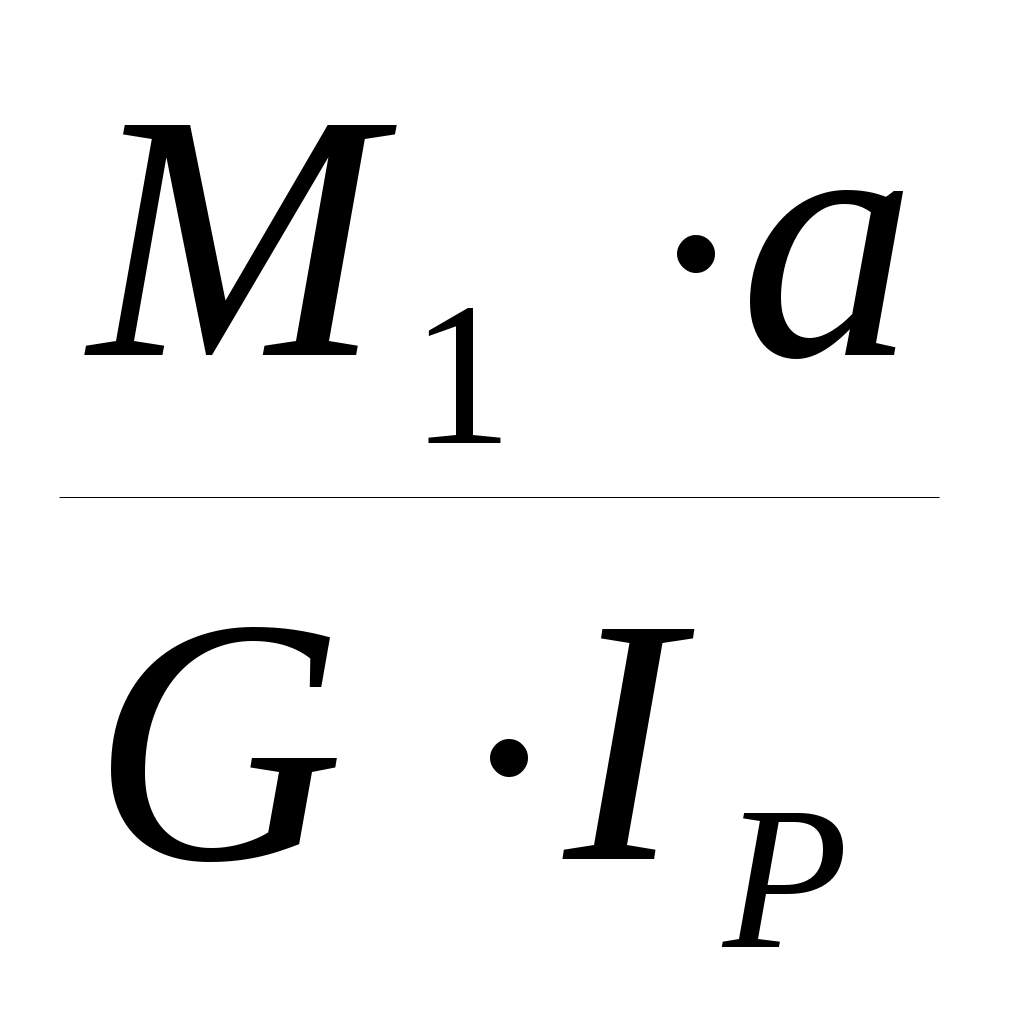
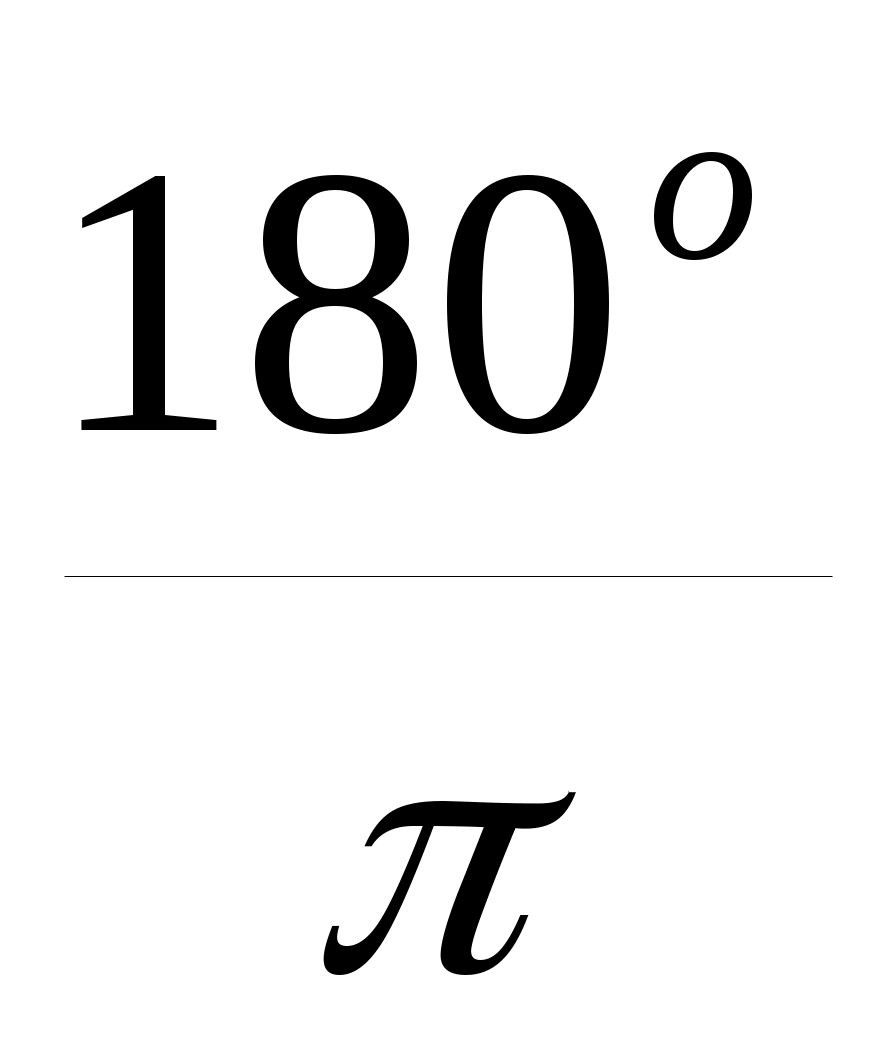 =-0,0015
=-0,0015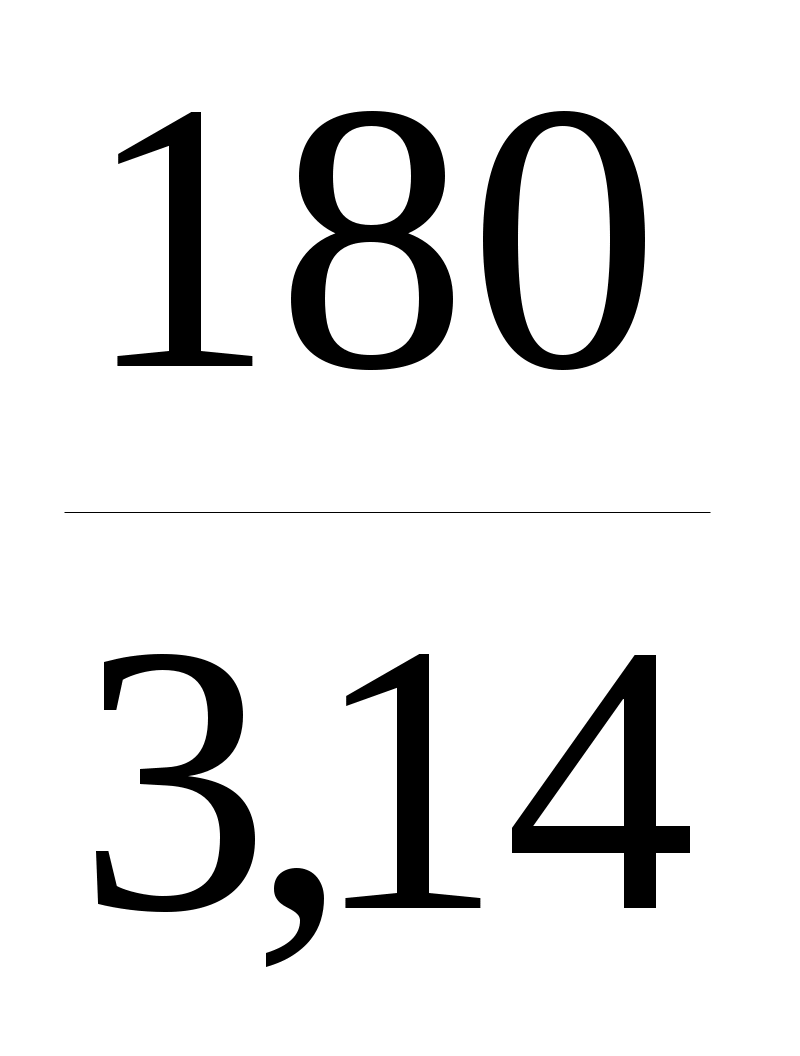 =0,09.
=0,09.
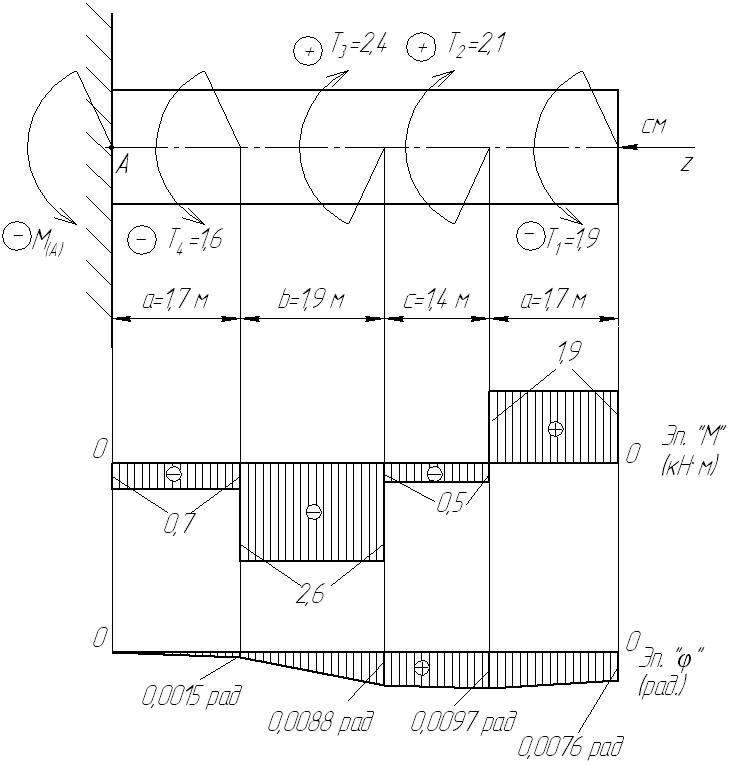
Задача 4. Изгиб. Статически определимые балки и рамы.
Условие и порядок выполнения задачи
На эпюрах должны быть проставлены числовые значения величин в характерных точках.
Для каждого участка балки записать уравнения определяемых величин и вычислить их значения для характерных точек.
- из условия прочности подобрать стальную балку двутаврового сечения;
- вычислить для этой балки максимальные значения нормального и касательного напряжений;
- в опасных сечениях построить эпюры изменения нормальных и касательных напряжений по высоте двутавровой балки;
- определить прогибы в характерных точках балки (середина пролёта, точки приложения сил, крайние точки на консолях);
- по найденным точкам построить изогнутую ось балки. Вычислить также угол поворота сечения на правой опоре.
Чертежи балок выполняются в произвольном масштабе.
3. В задаче 4а из условия прочности подобрать балку прямоугольного сечения из древесины при отношении высоты к ширине (h:b=4:1). Допускаемое нормальное напряжение для древесины принять равным 10 МПа.
F=26 кН; q=16 кН/м; М=26 кН∙м.
Длина участков: а=3,2 м; b=2,4 м; с=1,6 м.
Задача 4.
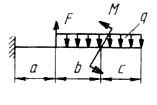
1. Определение опорной реакции.
R +F-qbc=0
+F-qbc=0
R = q(b+c)-F=16∙(2,4+1,6)-26=38 кН.
= q(b+c)-F=16∙(2,4+1,6)-26=38 кН.
Определение крутящего момента в точке А
-М -Fa-M+q(b+c)(a+
-Fa-M+q(b+c)(a+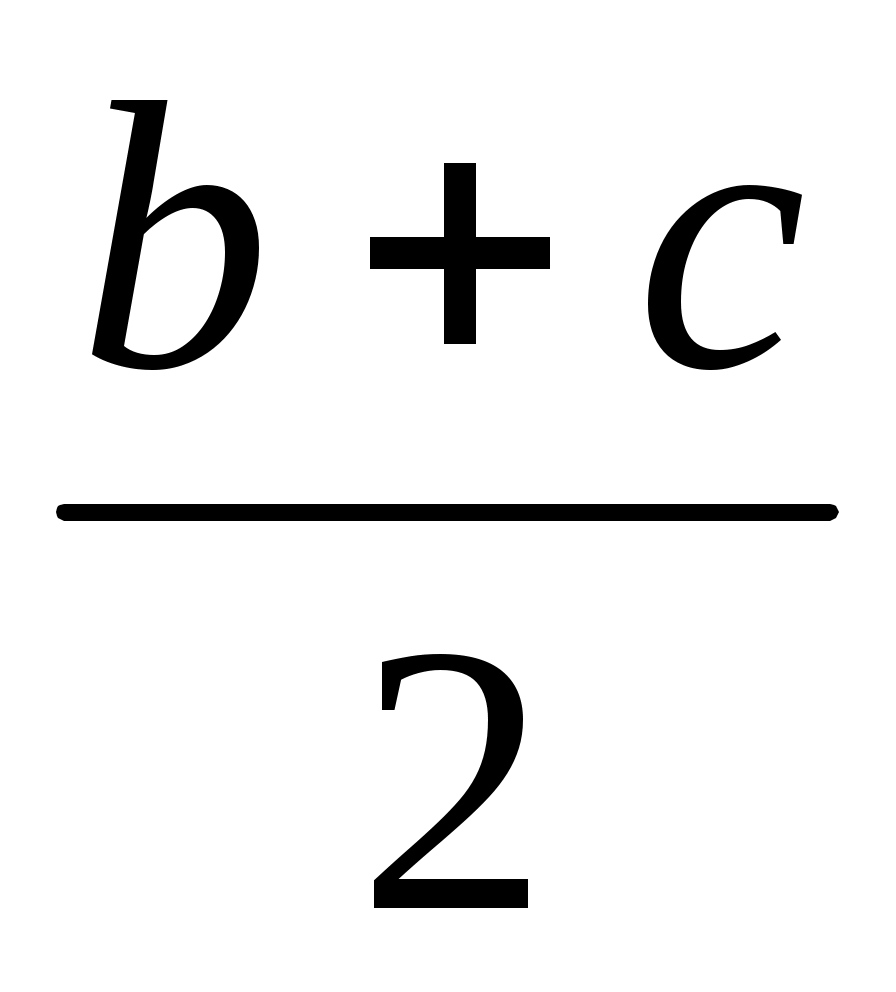 )=0
)=0
М =-Fa-M+q(b+c)(a+
=-Fa-M+q(b+c)(a+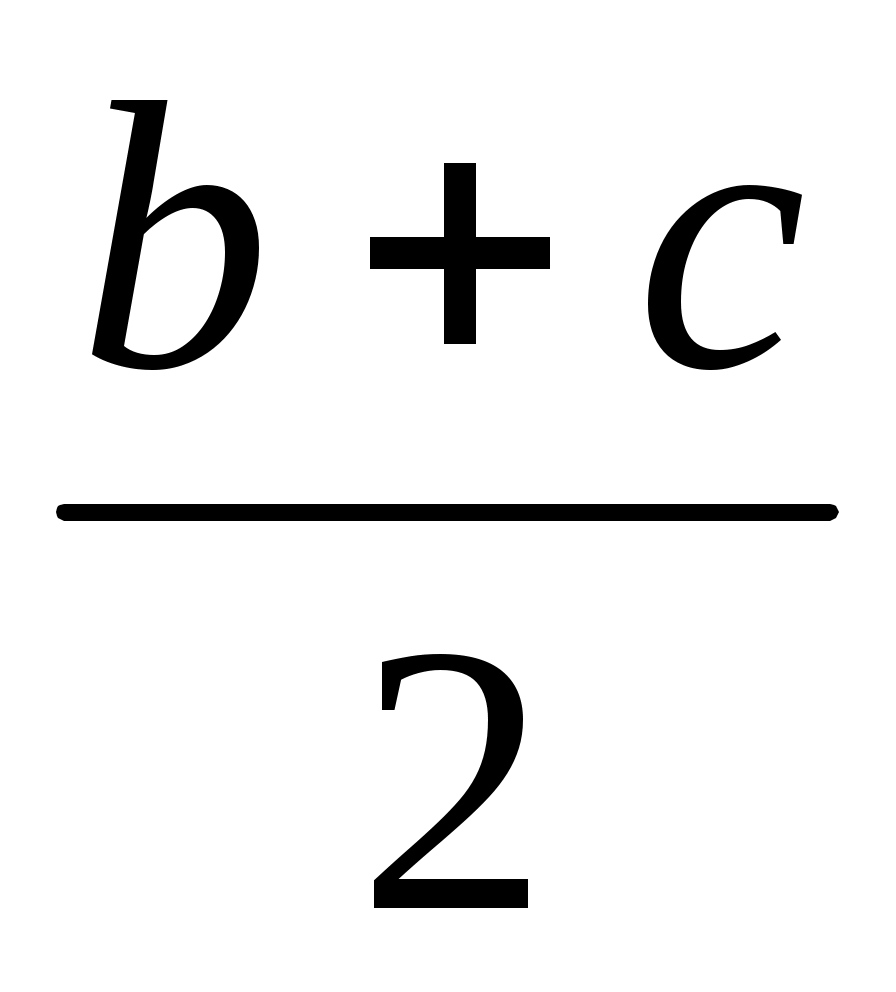 )= -26∙3,2-26+16∙(2,4+1,6)(3,2+
)= -26∙3,2-26+16∙(2,4+1,6)(3,2+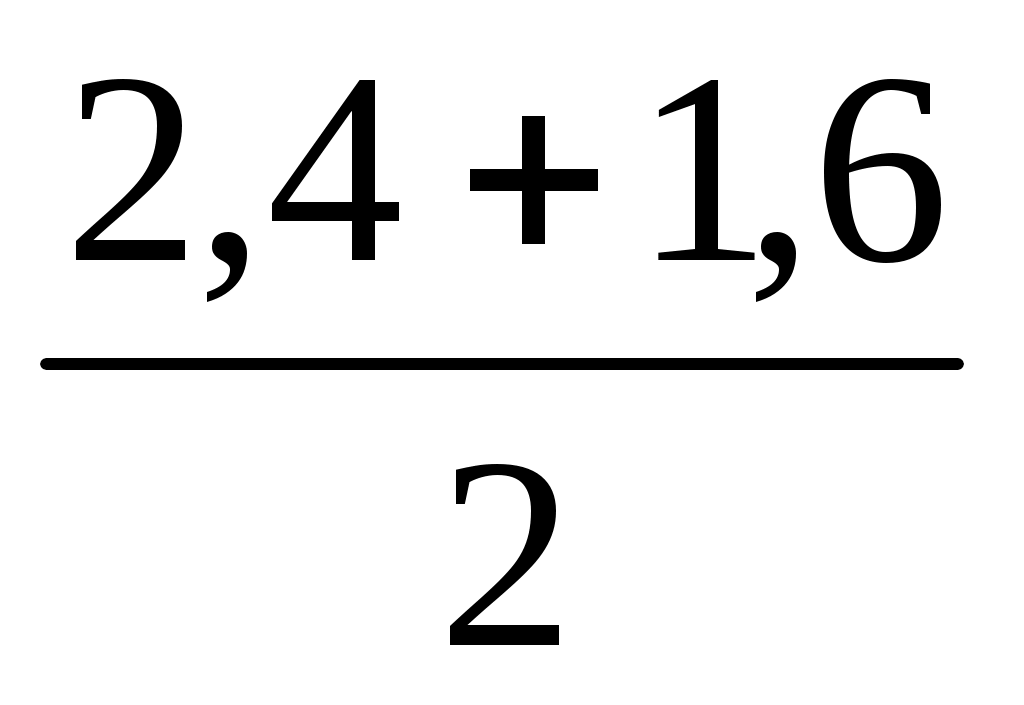 )=223,6 кН∙м.
)=223,6 кН∙м.
2. Определение внутренних силовых факторов методом сечений
Сечение I-I
0≤z ≤а
≤а
R -Q
-Q =0
=0
Q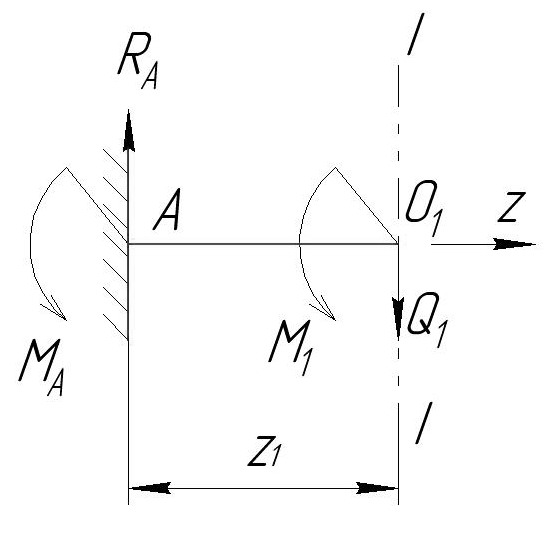
 = R
= R =38 кН.
=38 кН.
ΣМ(О )=0
)=0
- М -М
-М +R
+R z
z =0
=0
М = - М
= - М + R
+ R
z
z =0 М
=0 М =-223,6 кН∙м.
=-223,6 кН∙м.
z =а М
=а М = - 223,6+ 38∙3,2=-102 кН∙м.
= - 223,6+ 38∙3,2=-102 кН∙м.
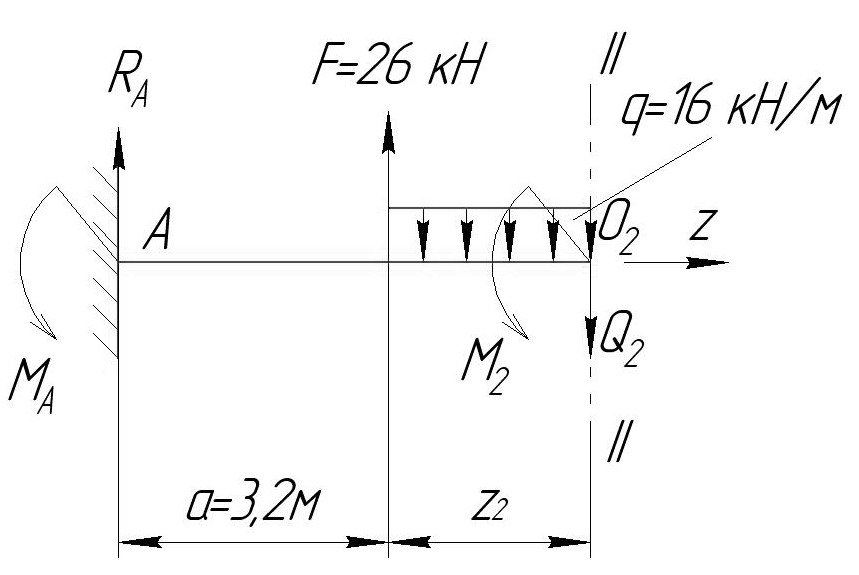
Сечение II-II
0≤z ≤b
≤b
R +F-q∙z
+F-q∙z -Q
-Q =0
=0
Q = R
= R +F-q∙z
+F-q∙z
z =0 Q
=0 Q = R
= R +F=38+26=64 кН
+F=38+26=64 кН
z =b Q
=b Q = R
= R +F-q∙b=38+26-16∙2,4=25,6 Н
+F-q∙b=38+26-16∙2,4=25,6 Н
ΣМ(О )=0
)=0
- М -М
-М +R
+R (а+z
(а+z )+Fz
)+Fz -q z
-q z z
z
/2=0
М = -М
= -М +R
+R (а+z
(а+z )+Fz
)+Fz -q z
-q z z
z /2=-223,6+38∙(а+z
/2=-223,6+38∙(а+z )+Fz
)+Fz -q z
-q z z
z /2=
/2=
z =0 М
=0 М = -М
= -М +R
+R а=-223,6+38∙3,2=-102 кН∙м.
а=-223,6+38∙3,2=-102 кН∙м.
z =b М
=b М =-М
=-М +R
+R (а+b)+Fb-q b
(а+b)+Fb-q b /2=-223,6+38(3,2+2,4)+26∙2,4-16∙2,4
/2=-223,6+38(3,2+2,4)+26∙2,4-16∙2,4 /2=5,52 кН∙м.
/2=5,52 кН∙м.
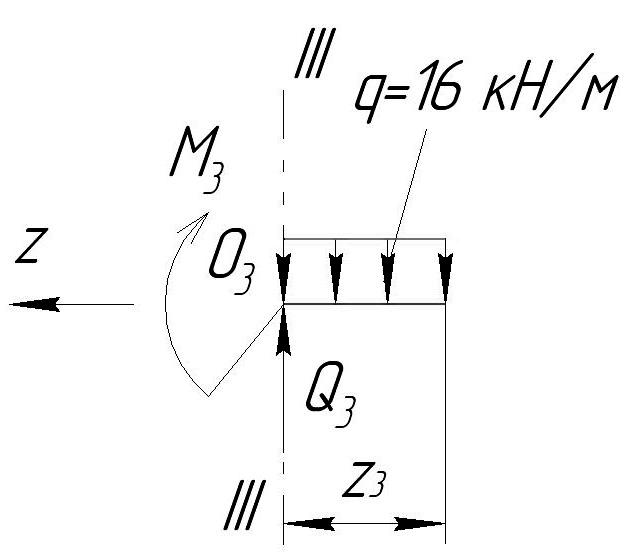
Сечение III-III
0≤z ≤с
≤с
Q -q z
-q z =0
=0
Q = q z
= q z
z =0 Q
=0 Q =0
=0
z =c Q
=c Q = q c=16∙1,6=25,6 кН
= q c=16∙1,6=25,6 кН
ΣМ(О )=0
)=0
М +q z
+q z z
z /2=0
/2=0
М =-q z
=-q z z
z /2
/2
z =0 М
=0 М =0
=0
z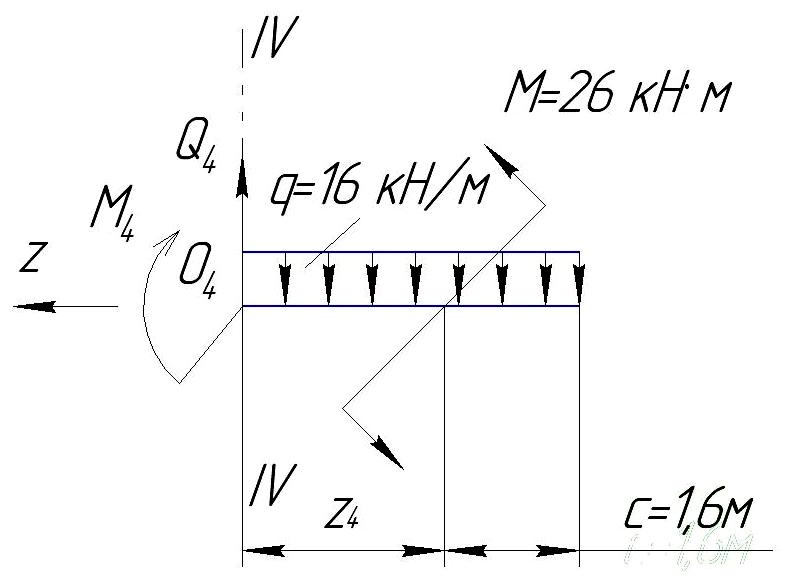
 =с М
=с М =-q с
=-q с /2=-16∙1,6
/2=-16∙1,6 /2=-20,5 кН.
/2=-20,5 кН.
Сечение IV-IV
0≤z ≤с
≤с
Q -q (с+z
-q (с+z )=0
)=0
Q = q (с+z
= q (с+z )
)
z =0 Q
=0 Q =qс=16∙1,6=25,6 кН
=qс=16∙1,6=25,6 кН
z =b Q
=b Q
φ
5. Определение относительного угла закручивания, возникающего на валу;
φ

Задача 4. Изгиб. Статически определимые балки и рамы.
Условие и порядок выполнения задачи
-
Для заданной схемы статически определимой балки определить опорные реакции и построить эпюры поперечных сил и изгибающих моментов.
На эпюрах должны быть проставлены числовые значения величин в характерных точках.
Для каждого участка балки записать уравнения определяемых величин и вычислить их значения для характерных точек.
-
В задаче 4 дополнительно:
- из условия прочности подобрать стальную балку двутаврового сечения;
- вычислить для этой балки максимальные значения нормального и касательного напряжений;
- в опасных сечениях построить эпюры изменения нормальных и касательных напряжений по высоте двутавровой балки;
- определить прогибы в характерных точках балки (середина пролёта, точки приложения сил, крайние точки на консолях);
- по найденным точкам построить изогнутую ось балки. Вычислить также угол поворота сечения на правой опоре.
Чертежи балок выполняются в произвольном масштабе.
3. В задаче 4а из условия прочности подобрать балку прямоугольного сечения из древесины при отношении высоты к ширине (h:b=4:1). Допускаемое нормальное напряжение для древесины принять равным 10 МПа.
F=26 кН; q=16 кН/м; М=26 кН∙м.
Длина участков: а=3,2 м; b=2,4 м; с=1,6 м.
Задача 4.

1. Определение опорной реакции.
R
R
Определение крутящего момента в точке А
-М
М
2. Определение внутренних силовых факторов методом сечений
Сечение I-I
0≤z
R
Q

ΣМ(О
- М
М
z
z
z

Сечение II-II
0≤z
R
Q
z
z
ΣМ(О
- М
/2=0
М
z
z

Сечение III-III
0≤z
Q
Q
z
z
ΣМ(О
М
М
z
z

Сечение IV-IV
0≤z
Q
Q
z
z