Файл: Задача Геометрические характеристики плоских сечений.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Решение задач

Дисциплина: Не указана

Добавлен: 08.11.2023

Просмотров: 77

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


I = - =

= - =-529 см .
7. Определение моментов сопротивления относительно главных центральных осей (U,V):
W = = =252 см .

W = = =65,1 см .
8. Определение радиусов инерции (i) относительно центра тяжести:
i =± =± =±7 см;

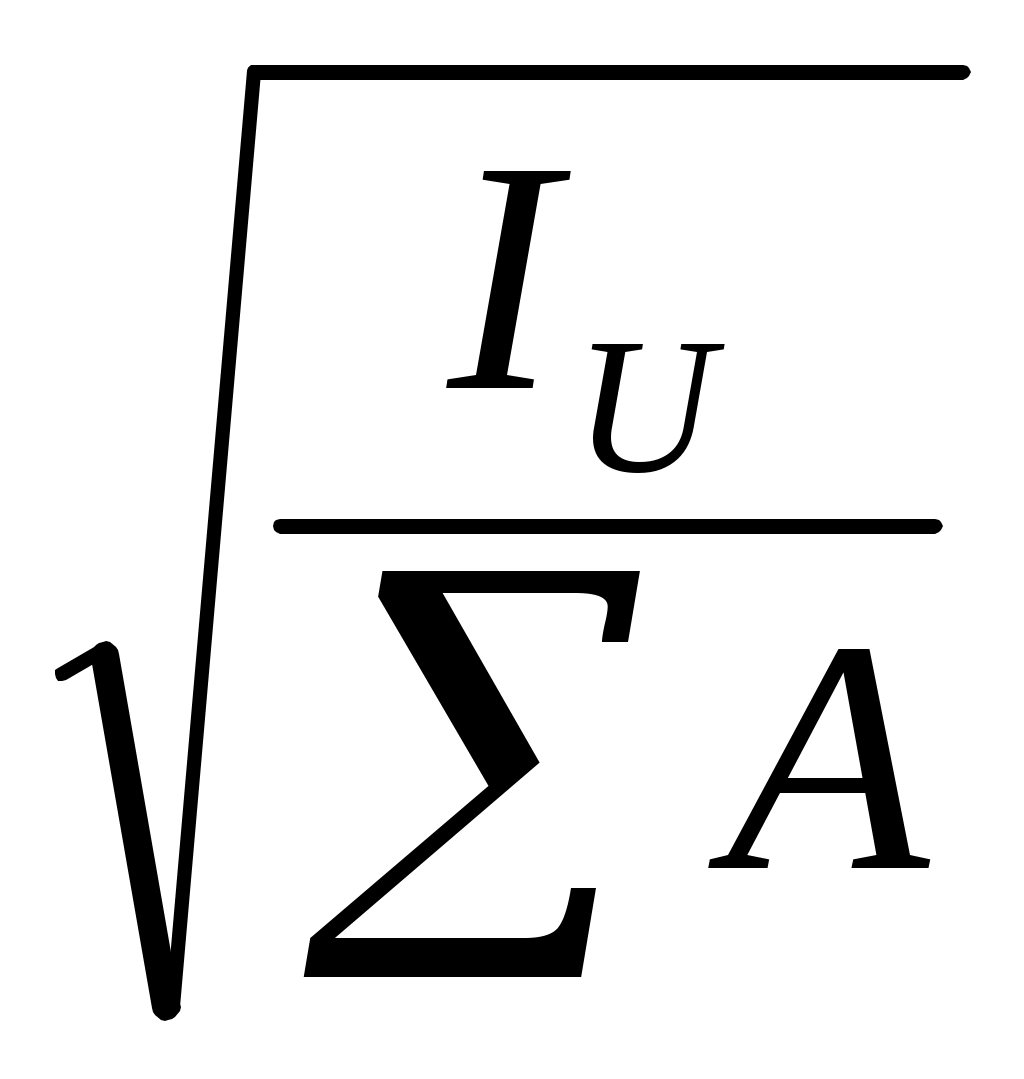i =± =± =±3,43 см.
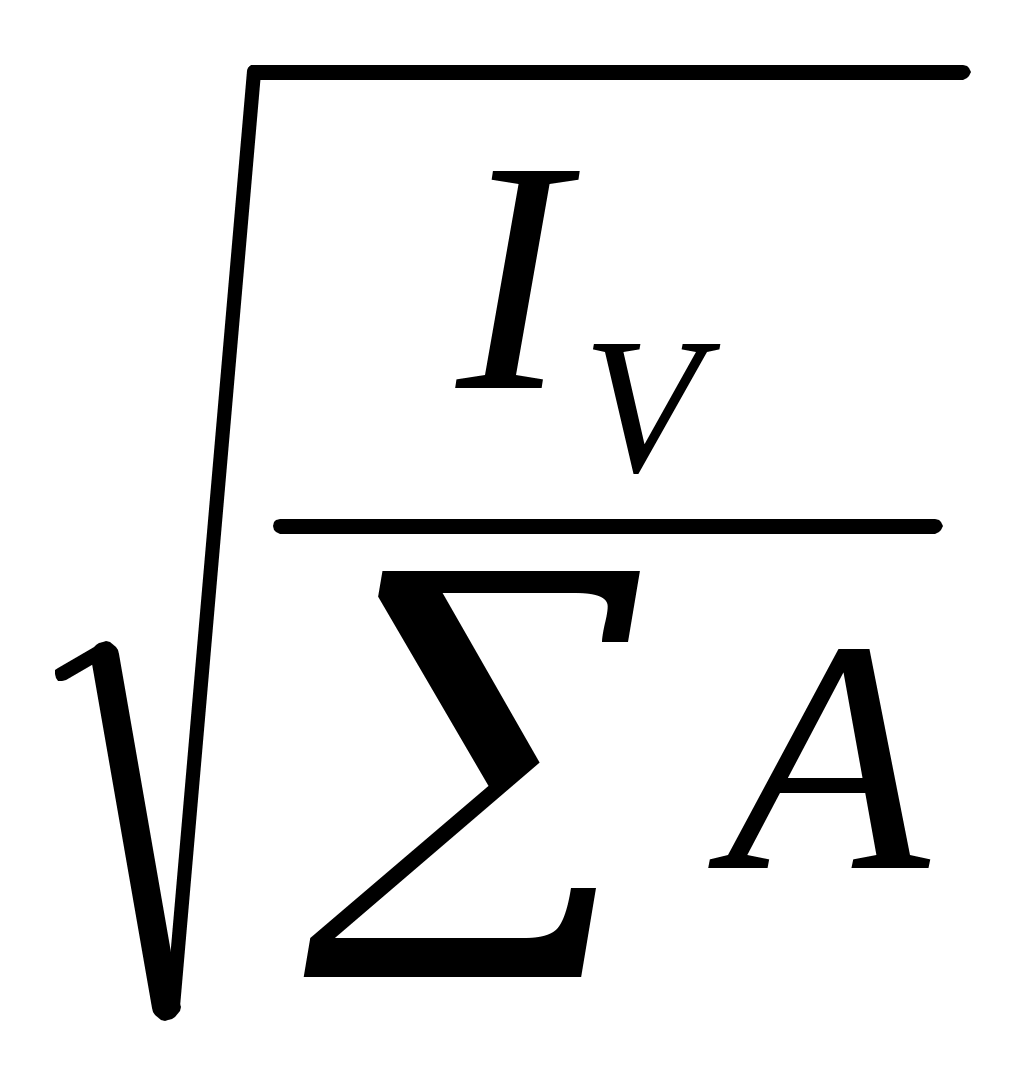9. Проверка:
| I |+| I |=|I |+|I |,

2135,1+599,6=2205,6+529

2735=2735 (см )



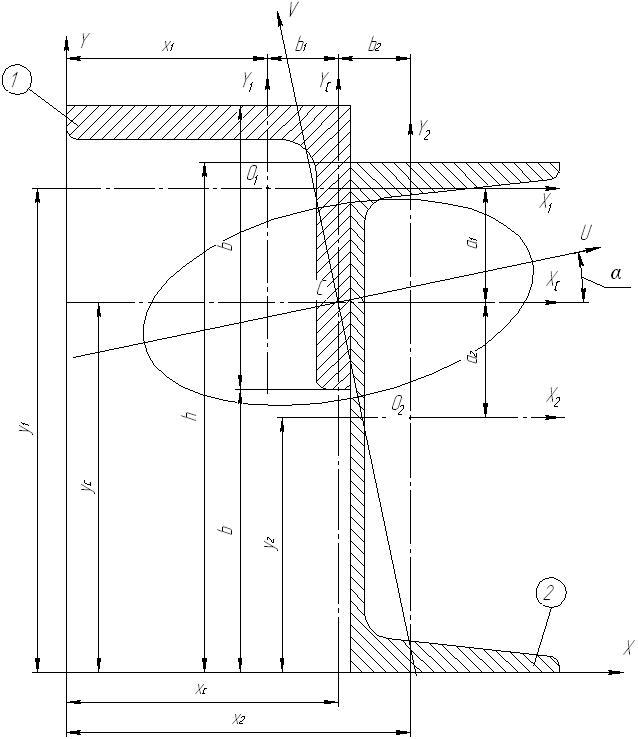
Задача 2. Растяжение прямых стержней. Определение напряжений и деформаций
Условие и порядок выполнения работы.


  1. Стальной стержень ступенчатого сечения находится под действием внешней силы и собственного веса.

  2. Необходимо построить эпюры:

- нормальных продольных сил;

- нормальных напряжений;

- перемещения сечений стержня относительно жёсткой заделки.

Площадь большего поперечного сечения стержня в 2 раза превышает меньшую.

Модуль продольной упругости для стали принимается равным:
Е=2∙10
МПа,

удельный вес γ=78 кН/м ;

нагрузка F=1,7 кН;

площадь меньшего сечения А=2,1 см

длины участков: а=22 м, с=14 м.



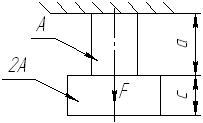
Решение.
1. Для определения внутренних усилий разбиваем стержень на отдельные участки, начиная от свободного конца.

Границами участков являются сечения, в которых приложены внешние силы, и место изменения размеров поперечного сечения. Таким образом, заданный стержень имеет два участка.

Применяя метод сечения, будем оставлять нижнюю часть и отбрасывать верхнюю отсечённую часть стержня.
2. Определение реакции опоры R в жёсткой заделке в точке А

ΣF(z)=0;

-R +G +G +F=0;

R = G +G +F;

G =γ∙А∙а=78∙2,1∙10 ∙22=0,36 кН;

G = γ∙2А∙b=78∙2∙2,1∙10 ∙14=0,459 кН.

R =0,36+0,459+1,7=2,519 кН.

3. Определение продольной силы N в сечениях стержня методом сечения.

П
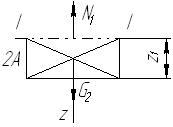
роведём продольное сечение на участке I-I.
Сечение I-I
ΣF(z)=0 при 0≤z ≤c

-N +G =0

при z =0 N =G = γ∙2А∙ z =0

при z =с N =G = γ∙2А∙ с=78∙2∙2,1∙10 ∙14=0,459 кН.
Сечение II-II


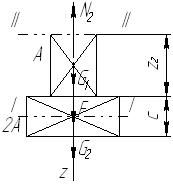
ΣF(z)=0 при 0≤z ≤а

-N +G =0

при z =0 N =G +F+G =

= γ∙2А∙c+F+ γ∙А∙z =78∙2∙2,1∙10 ∙14+1,7+78∙2,1∙10 ∙0=2,159 кН;

при z =а N = G +F+G
=

= γ∙2А∙c+F+ γ∙А∙а=78∙2∙2,1∙10 ∙14+1,7+78∙2,1∙10 ∙22=2,519 кН.
Построим эпюру, показывающую как меняется N по длине стержня.

4. Определение нормальных напряжений σ, возникающих в сечениях стержня;
Сечение I-I

σ = =0;

σ = = =1093 кН/м =1,093 МПа.
Сечение II-II

σ = = =10280 кН/м =10,28 МПа;

σ = = =11995 кН/м =12 МПа.


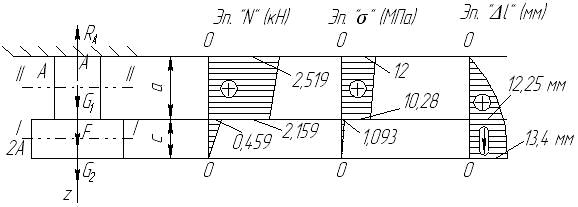
5. Определение удлинения (перемещения) Δl сечений после деформации:
Δl=0
Δl = + = + =1,131+0,094=1,225 см;

Δl = Δl +

Смотрите также файлы