Файл: Требуется рассчитать плоскоременную передачу с натяжным роликом (рисунок 1).doc

Задание 1Требуется рассчитать плоскоременную передачу с натяжным роликом (рисунок 1).

Исходные данные: - мощность на ведущем валу N1 = 8 кВт; - угловая скорость ведущего шкива ω1 = 144 с-1; - угловая скорость ведомого шкива ω2 = 32 с-1. Определяем частоты вращения шкивов (n1 и n2) Определяем передаточное число u' = ω1 / ω2 = 144 / 32 = 4,5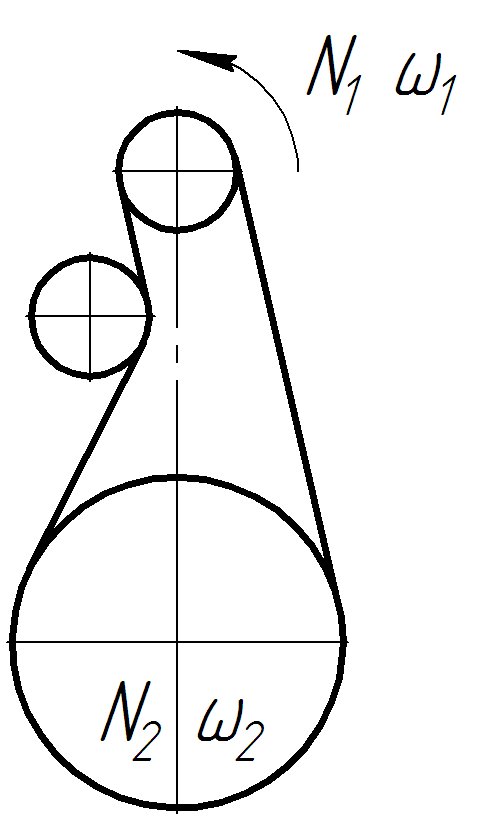

Рисунок 1 – Схема передачи

Определяем предварительный диаметр ведущего шкиваd₁ = (35…70) ∙ δ = (35…70) ∙ 2,8 = 98 … 196 ммгде δ = 2,8 мм – толщина ремня [1, с. 80, таблица 5.1].Принимаем стандартный диаметр d₁ = 180 мм [1, с. 448, таблица К40].Определяем предварительный диаметр ведомого шкиваd₂ = u'·d₁(1 – ε) = 4,5·180·(1 – 0,015) = 798 ммПринимаем стандартный диаметр d₂ = 800 мм [1, с. 448, таблица К40].Определяем диаметр натяжного роликаd₀ = d₁ … 0,8 ∙ d₁ = 180 … 0,8 ∙ 180 = 180 … 144 ммПринимаем стандартный диаметр d₀ = 160 мм [1, с. 448, таблица К40].Определяем фактическое передаточное число и его отклонение от требуемого (Δu ≤ 3%) ; Определяем минимальное межосевое расстояние для передачи с натяжным роликома ≥ d₁ + d₂ = 180 + 800 = 980 ммПринимаем межосевое расстояние a = 1135 мм.Помещать ролик желательно на ведомой ветви так, чтобы угол огибания его ремнем был не более 120°, а центр ролика располагался от центра малого шкива на расстоянииA ≥ d₀ + (0,5…1) ∙ d₁ = 160 + (0,5…1) ∙ 180 = 250 … 340 ммПринимаем A = 300 мм.Для определения точного положения натяжного ролика на ведомой ветви зададимся стандартной длиной ремня = 4000 мм [1, с. 81].Вычерчиваем схему передачи в масштабе 1:10 (рисунок 2). По вычерченной в масштабе схеме передачи, определяем углы α

---

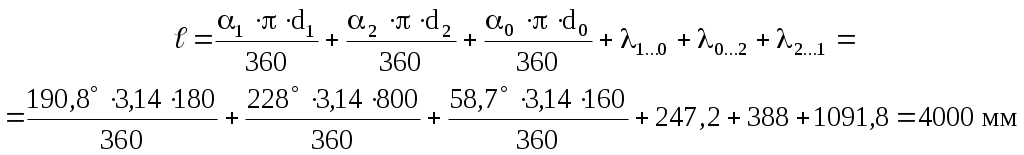
₁ = 190,8°, α₂ = 228°, α₀ = 58,7° и длины прямолинейных участков λ_1…0 = 247,2 мм, λ_0…2 = 688 мм и λ_2…1 = 1091,8 мм.Проверяем длину ремня, одновременно уточняя положение натяжного роликаОпределяем скорость ремня, сравнивая ее с допускаемой [ ]=35 м/с [1, с. 81] < 35 м/сгде d₁ = 0,18 м – диаметр ведущего шкива.Определяем частоту пробегов ремня, сравнивая ее с допускаемой [U]=15 с^-1 [1, с. 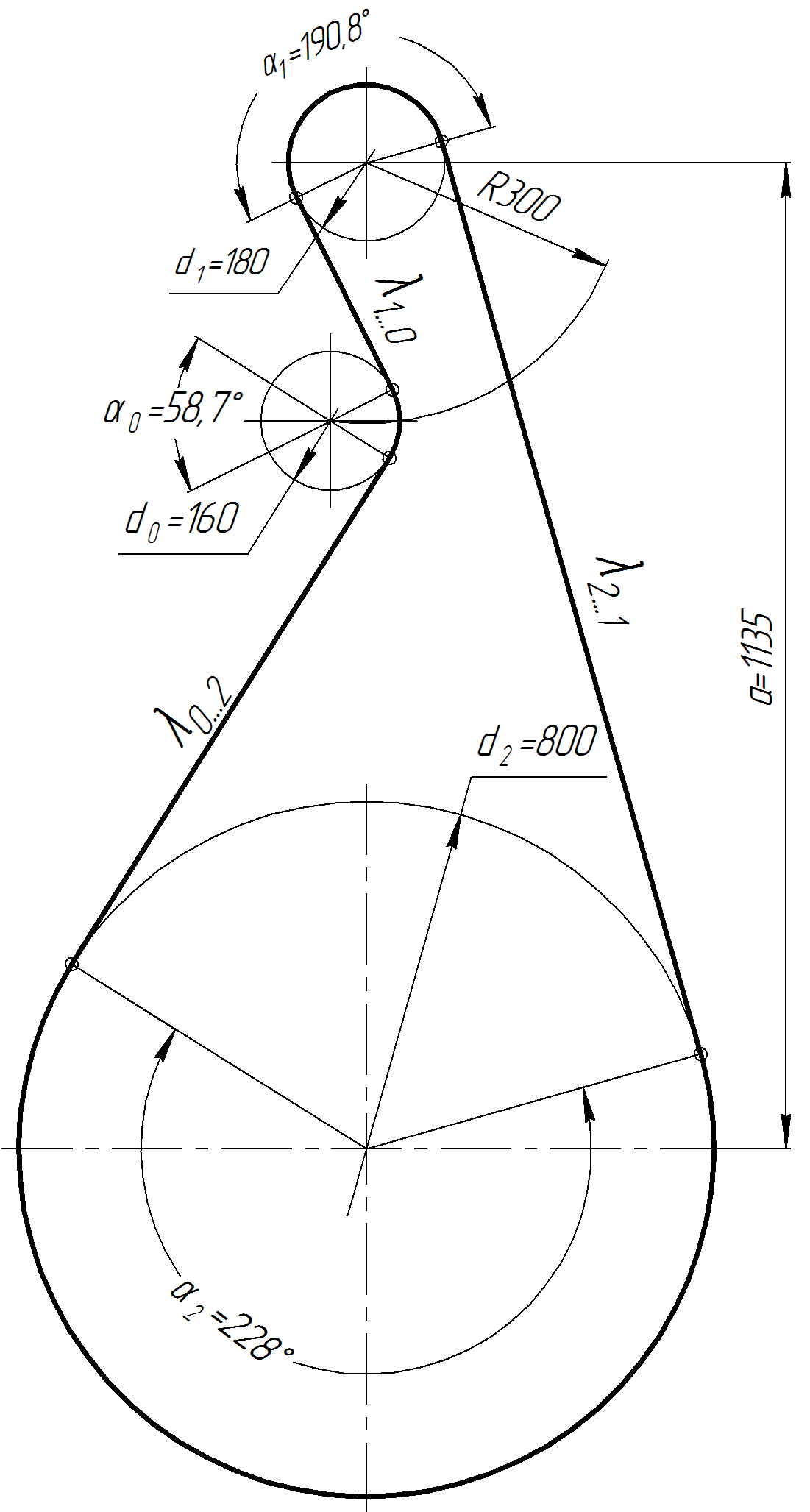82] < 15 с^-1Рисунок 2 – Схема передачи (1:10)Рассчитываем окружную силу, растягивающую ремниF_t = N₁ / = 8·10³ / 13 = 615,4 НОпределяем допускаемую удельную окружную силу[k_п] = [k₀] ∙ С_θ ∙ С_α ∙ С ∙ С_р ∙ С_d ∙ С_F = 1,6 ∙ 0,8 ∙ 1 ∙ 0,97 ∙ 0,8 ∙ 1,2 ∙ 0,85 = 1,0 МПагде [k₀] = 1,6 МПа [1, с. 80, таблица 5.1] – допускаемая приведенная удельная окружная сила;С_θ = 0,8 [1, с. 82, таблица 5.2] – коэффициент от угла наклона линии центров шкивов к горизонту;С_α = 1 [1, с. 82, таблица 5.2] – коэффициент от угла обхвата ведущего шкива;С = 0,97 [1, с. 82, таблица 5.2] – коэффициент от центробежной силы;С_р = 0,8 [1, с. 82, таблица 5.2] – коэффициент от динамичности нагрузки и длительности работы (работа в две смены с умеренными колебаниями нагрузки);С_d = 1,2 [1, с. 83, таблица 5.2] – коэффициент от диаметра меньшего шкива;С_F = 0,85 [1, с. 83, таблица 5.2] – коэффициент от неравномерности распределения нагрузки между кордшнурами плоского ремня.Определяем минимальную ширину ремняПринимаем хлопчатобумажный цельнотканый пропитанный ремень шириной b=220 мм. Шкивы принимаем шириной 240 мм.Определяем площадь поперечного сечения ремня

---

А = δ ∙ b = 2,8 ∙ 220 = 616 мм²Определяем силу предварительного натяжения ремняF₀ = A ∙ σ₀ = 616 ∙ 2 = 1232 Нгде σ₀ = 2 МПа [1, с. 80, таблица 5.1] – предварительное натяжение.Определить силы натяжения ведущей (F₁) и ведомой (F₂) ветвей ремняF₁ = F₀ + 0,5 ∙ F_t = 1232 + 0,5 ∙ 615,4 = 1540 НF₂ = F₀ – 0,5 ∙ F_t = 1232 – 0,5 ∙ 615,4 = 924 НОпределить силу давления ремня на валРассчитываем напряжение от силы натяжения ведущих ветвейσ₁ = F₁ / А = 1540 / 616 = 2,5 МПаРассчитываем напряжение от изгибаσ_и = Е_И · δ / D₁ = 100 · 2,8 / 180 = 1,56 МПагде Е_И = 100 МПа [1, с.123] – условный модуль упругости материала ремня.Рассчитываем напряжение от центробежной силыσ = ρ · ² · 10^-6 = 1200 · 13² · 10^-6 = 0,2 МПагде ρ = 1200 кг/м³ [1, с.123] – плотность материала ремня.Рассчитываем максимальное напряжение в сечении ремня, сравнивая его с допускаемым [σ]_Р = 8 МПа [1, с. 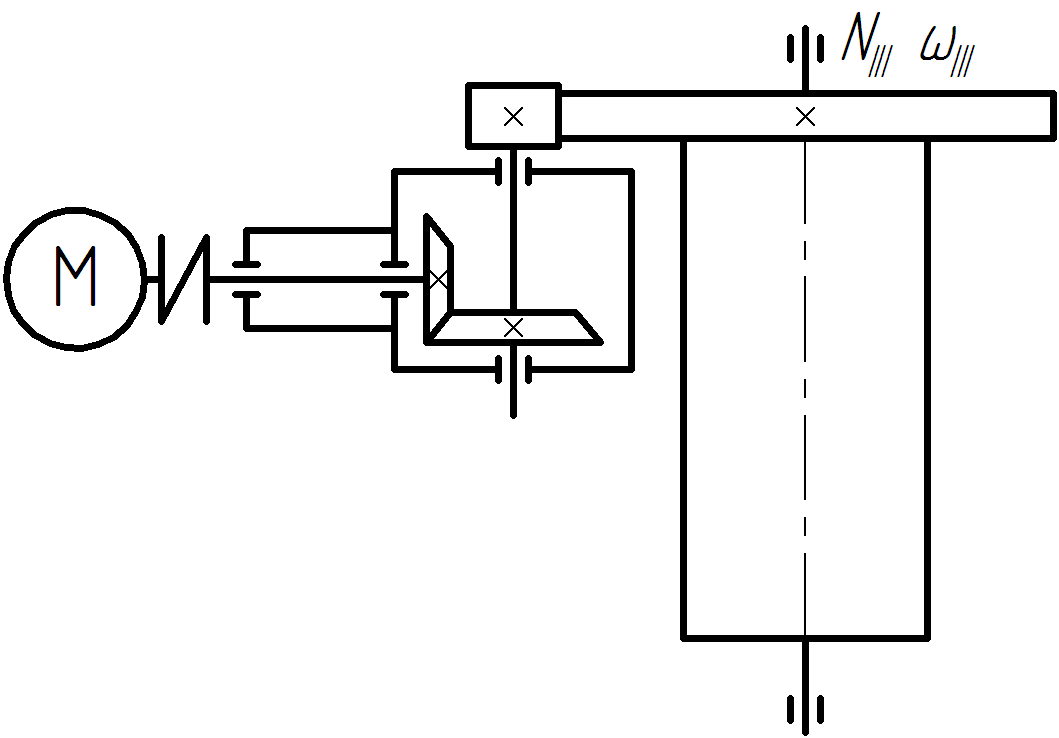85]σ_max = σ₁ + σ_и + σ = 2,5 + 1,56 + 0,2 = 4,3 МПа < 8 МПаЗадание 2Требуется рассчитать механические передачи привода (рисунок 2).Рисунок 2 – Схема передачиИсходные данные:- мощность на ведомом валу N_III = 5 кВт;- угловая скорость ведомого вала ω_III = 5 с^-1.- передаточное отношение привода u = 14.Определяем угловую скорость ведущего валаω_I = ω_I ∙ u = 5 ∙ 14 = 70 с^-1;По кинематической схеме определяем общий КПД приводаη_общ = η_к · η_з · η_м · η^k_пк = 0,97 · 0,97 · 0,98 · 0,99³ = 0,9где Ση_i – КПД элементов, составляющих привод [1, с. 61, таблица 7]η_к = 0,97 – КПД конической передачи;η_з = 0,97 – КПД цилиндрической передачи;η_м = 0,98 – КПД муфты;η_п = 0,99 – КПД одной пары подшипников качения.k = 3 – число пар подшипников качения.Определяем требуемую мощность электродвигателяN_Э.тр = N_III / η_общ = 5 / 0,9 = 5,56 кВтОпределяем частоты вращения валов (n₁ и n₃)

---

Предварительно принимаем передаточное число конической передачи u_к=4,5, тогда передаточное число цилиндрической передачиu_з = u / u_к = 14 / 4,5 = 3,1Принимаем u_з = 3,15.Вычисляем фактическое значение передаточного отношения приводаu = u_к · u_з = 4,5 · 3,15 = 14,175Определяем отклонение от требуемого (допускается расхождение 5%)Определяем частоты вращения валовn_I = n_эд = 668,5 мин^-1n_II = n_I / u_к = 668,5 / 4,5 = 148,6 мин^-1n_III = n_II / u_ч = 148,6 / 3,15 = 47,2 мин^-1Определяем мощности на валах приводаN_III = 5 кВтN_II = N_III / (η_з · η_п) = 5 / (0,97 · 0,99) = 5,2 кВтN_I = N_II / (η_к · η_п) = 5,2 / (0,97 · 0,99) = 5,4 кВтОпределяем вращающие моменты на валах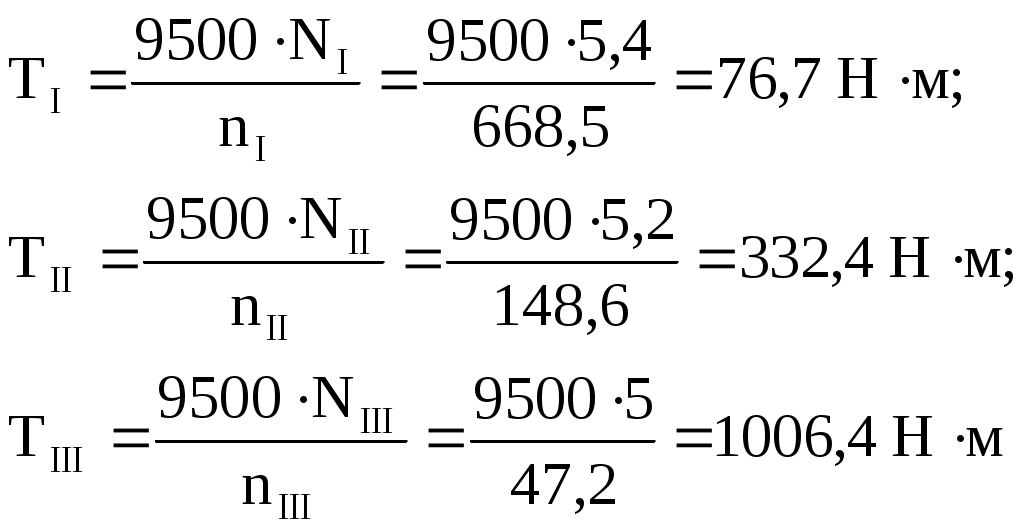Исходные данные для расчета конической передачи редуктора:- вращающие моменты Т₁ = 76700 Н·ммТ₂ = 332400 Н·мм.- частоты вращения n₁ = 668,5 мин^-1; n₂ = 148,6 мин^-1.- требуемое передаточное число u = 4,5.Примем для шестерни и колеса одну и ту же марку стали с различной термообработкой: для шестерни сталь 40Х улучшенную с твердостью НВ 270; для колеса сталь 40Х улучшенную с твердостью НВ 245 [2, с. 34, таблица 3.3].Определяем допускаемые контактные напряжения:где σ_Hlimb = 2НВ + 70 = 2245 + 70 = 560 МПа [2, с. 34, таблица 3.2] – предел контактной выносливости материала колеса;K_HL = 1 [2, с. 33] - коэффициент долговечности при длительной эксплуатации;[S_H] = 1,1 - коэффициент безопасности [2, с. 33].Принимаем коэффициент, учитывающий неравномерность распределения нагрузки по ширине зуба при консольном расположении шестерни К_Н = 1,35 [2, с. 32, таблица 3.1.].Принимаем коэффициент ширины венца по отношению к внешнему конусному расстоянию _bRe = 0,285 [2, с. 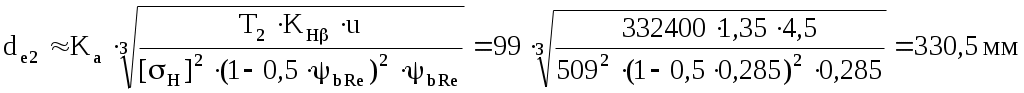49].Определяем внешний делительный диаметр колеса по условию контактной прочности активных поверхностей зубьевгде К_а = 99 [2, с. 49] – коэффициент для прямозубых передач.Определяем число зубьев колеса, приняв число зубьев шестерни z

---

₁ = 20z₂ = z₁u = 20  4,5 = 90Определяем внешний окружной модуль мм (округляем до 4 мм)Определяем углы делительных конусов₂ = аrctg u = аrctg 4,5 = 77°28’;₁ = 90° – ₂ = 90° – 77°28’ = 12°32’.Определяем внешнее конусное расстояние R_e и длину зуба b: мм;b = _bReR_e = 0,285184,4 = 52,6 мм (принимаем b = 55).Уточняем внешние делительные диаметрыd_e1 = m_e  z₁ = 4  20 = 80 мм.d_e2 = m_e  z₂ = 4  90 = 360 мм.Определяем средний делительный диаметр шестерни и колесаd₁ = 2 (R_e – 0,5b)  sin₁ = 2 (184,4 – 0,555)  sin12°32’= 68,1 ммd₂ = 2 (R_e – 0,5b)  sin₂ = 2 (184,4 – 0,555)  sin77°28’= 306,32 ммОпределяем внешние диаметры шестерни и колеса (по вершинам зубьев)d_ae1 = d_e1 + 2m_ecos₁ = 80 + 24cos1232’ = 87,81 мм.d_ae2 = d_e2 + 2m_ecos₂ = 360 + 24cos7728’ = 361,74 мм.Определяем средний окружной модуль мм.Определяем коэффициент ширины шестерни по среднему диаметруОпределяем среднюю окружную скорость колес м/сНазначаем 7-ю степень точности передачи.Для проверки контактных напряжений уточняем коэффициент нагрузки:К_Н = К_Н К_Н К_НV = 1,3  1,0  1,05 = 1,37где К_Н= 1,3 [2, с. 39, таблица 3.5] – коэффициент, учитывающий распределение нагрузки по длине зуба при _bd = 0,8, консольном расположении колёс и твёрдости НВ<350;К_Н= 1,0 [2, с. 39, таблица 3.4] – коэффициент, учитывающий распределение нагрузки между прямыми зубьями;К_НV = 1,05 [2, с. 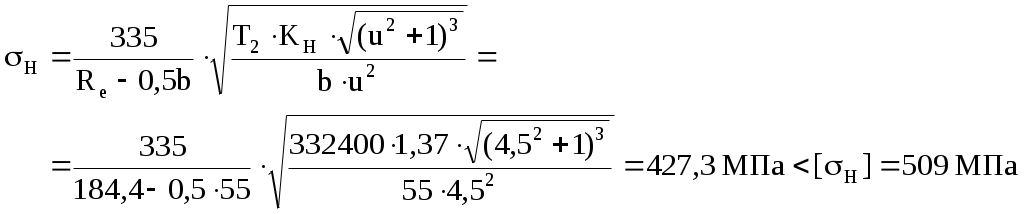40, таблица 3.6] – коэффициент, учитывающий динамическую нагрузку в зацеплении для прямозубых колёс при ≤ 5 м/с.Проверяем контактное напряжение на активных поверхностях зубьевОпределяем окружную силу в зацеплении:

---