Файл: Шпоры переделан.docx

28. Метод вращения Якоби

Метод применяется для решения стандартной задачи на собственные значения. Для начала введем понятия малой и большой задачи:

• малая задача - это когда матрица решаемой задачи располагается целиком во внешней памяти;

• большие задачи обычно распадаются на малые, которые решаются стандартно.

Рассматриваем малую задачу.

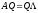- Стандартная задача на собственные значения.

где

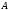- известная матрица

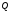- матрица поворота

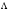- собственные числа матрицы А

Суть метода Якоби:

Метод Якоби заключается в том, чтобы подобрать матрицу Q, удовлетворяющую уравнению (2). Из условия ортогональности (1) следует:

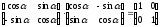
Реализация:

В зависимости от угла делаем величины внедиагональных элементов матрицы А как можно меньше:

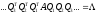
Если внедиагональные элементы стали меньше заданного числа, то можно считать, что задача решена с определенной степенью точности.

Также отметим, что:

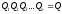
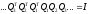
29. Методы решения систем линейных и нелинейных алгебраических уравнений.

Вычисления при решении систем обыкновенных дифференциальных уравнений (СОДУ) состоят из нескольких вложенных один в другой циклических процессов. Внешний цикл — цикл пошагового численного интегрирования, параметром цикла является номер шага. Если модель анализируемого объекта нелинейна, то на каждом шаге выполняется промежуточный цикл — итерационный цикл решения системы нелинейных алгебраических уравнений (СНАУ). Параметр цикла — номер итерации. Во внутреннем цикле решается система линейных алгебраических уравнений (СЛАУ)

. Поэтому в математическое обеспечение анализа на макроуровне входят методы решения СНАУ и СЛАУ.

Для решения систем алгебраических уравнений можно применять прямые итерационные методы. К ним относятся методы простой итерации, Зейделя, Якоби, релаксации. Для них необходимо выполнение довольно жестких условий сходимости, характерна сравнительно медленная сходимость.

Поэтому в современных программах анализа наибольшее распространение получил метод Ньютона, основанный на линеаризации СНАУ. Собственно модель получена именно в соответствии с методом Ньютона. Основное преимущество метода Ньютона — высокая скорость сходимости.

Вычислительный процесс стартует с начального приближения и в случае сходимости итераций заканчивается, когда погрешность станет меньше допустимой погрешности .

Однако метод Ньютона не всегда приводит к сходящимся итерациям. Условия сходимости метода Ньютона выражаются довольно сложно, но существует легко используемый подход к улучшению сходимости. Это близость начального приближения к искомому корню СНАУ. Использование этого фактора привело к появлению метода решения СНАУ, называемого продолжением решения по параметру.

В методе продолжения решения по параметру в ММС выделяется некоторый параметр , такой, что прикореньсистемы (2) известен, а при увеличенииотдо его истинного значения составляющие вектораплавно изменяются отдо истинного значения корня. Тогда задача разбивается на ряд подзадач, последовательно решаемых при меняющихся значениях, и при достаточно малом шагеизмененияусловия сходимости выполняются.

В качестве параметра можно выбрать некоторыйвнешний параметр, например, при анализе электронных схем им может быть напряжение источника питания. Но на практике при интегрировании СОДУ в качестве выбирают шаг интегрирования. Очевидно, что прикорень СНАУ равен значению вектора неизвестных на предыдущем шаге. Регулирование значенийвозлагается на алгоритмавтоматического выбора шага.

В этих условиях очевидна целесообразность представления математических моделей для анализа статических состояний в виде СОДУ, как и для динамического анализа.

К другим методам решения систем алгебраических уравнений, используемым в математическом обеспечении САПР, относятся методы простой итерации, Зейделя, Якоби, релаксации.

В соответствии с методом простой итерации вычисления выполняют по формуле

причем для обеспечения сходимости параметр нужно выбирать из условиядля любогогде—-е собственное значение матрицы Якоби.

Метод Зейделя отличается от метода простой итерации тем, что правая часть итерационной формулы обновляется сразу же после вычисления очередного элемента вектора .

30. Анализ в частотной области.

Анализ в частотной области более специфичен по сравнению с анализом во временной области. Его применяют, как правило, к объектам с линеаризуемыми математическими моделями при исследовании колебательных стационарных процессов, анализе устойчивости, расчете искажений информации, представляемой спектральными составляющими сигналов, и т.п.

Анализ в частотной области выполняется по отношению к линеаризованным моделям объектов. Для линейных систем дифференциальных туравнений справедливо применение для алгебраизации дифференциальных уравнений преобразования Фурье, в котором оператор заменяется на оператор.

Характерной особенностью получающейся систем линейных алгебраических уравнений (СЛАУ) является комплексный характер матрицы коэффициентов, что в некоторой степени усложняет процедуру решения, но не создает принципиальных трудностей. При решении задают ряд частот . Для каждой частоты решают СЛАУ и определяют действительные и мнимые части искомыхфазовых переменных. По ним определяют амплитуду и фазовый угол каждой спектральной составляющей, что и позволяет построить амплитудно-частотные, фазочастотные характеристики, найти собственные частоты колебательной системы и т.п.

31. Сравнение методов конечныx элементов и конечных разностей

Разработано много методов численного решения уравнений в частных производных. Наиболее часто используемые из них - методы конечных разностей и конечных элементов.             Метод конечных разностей был разработан раньше остальных и на первый взгляд является наиболее простым в реализации. Идея его состоит в разбиении прямоугольной сеткой области, в которой решается уравнение, и дискретизация дифференциального оператора. Решая линейную систему уравнений, находят приближенные решения в узлах решетки. Основные трудности связаны с учетом граничных условий, если граница области имеет сложную геометрическую форму.             Первые разработки метода конечных элементов (МКЭ) были выполнены в 50-х годах для решения задач сопротивления материалов. В 60-е годы математики получили строгие формулировки для этого метода, после чего он становится общим средством изучения задач в частных производных, понемногу вытесняя метод конечных разностей, который рассматривался в период своего апогея как универсальное средство решения задач такого типа. После подробного математического его исследования оказалось, что при негладких входных данных задачи МКЭ часто сходится быстрее, чем метод конечных разностей, а иногда вообще обладает оптимальной скоростью сходимости. Начиная с 1970 г. этот метод становится все более популярным среди инженеров всех специальностей благодаря работам Зинкевича, Галлагера, Одена, Лиона, Равьяра, Сильвестера.             Еще раз кратко остановимся на связях и сравнении МКЭ с методом конечных разностей, этих наиболее распространенных и эффективных численных методов. Построение конечно-разностных схем обычно требует небольшого объема вычислений, как правило, меньшего, чем в МКЭ. Однако достоинствами МКЭ являются гибкость и разнообразие сеток, стандартные приемы построения дискретных задач для произвольных областей, простота учета естественных краевых условий и т. д. Кроме того, математический анализ МКЭ является более простым, его методы применими к более широкому классу исходных задач, а оценки погрешностей приближенных решений, как правило, получаются при менее жестких ограничениях, чем в методе конечных разностей. Вместе с тем необходимо подчеркнуть, что основу для исследования МКЭ создали фундаментальные результаты, связанные с исследованием сходимости и устойчивости конечно-разностных схем, проекционных методов, обобщенных решений.